
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Робоча формула

 Розглянемо дифракцію Фраунгофера від двох щілин. Щілиною називають прямокутний отвір, шириною якого, порівняно з його довжиною, можна знехтувати. Нехай світлова хвиля, довжина якої λ, поширюється перпендикулярно до щілини, ширина якої а. Паралельний пучок світла, пройшовши крізь щілини, дифрагує під різними кутами φ від початкового напрямку (рис. 69.1). За щілинами розміщена лінза L, у фокальній площині якої знаходиться екран Е. На екрані спостерігається дифракційна картина – почергово розміщені світлі і темні смуги. Оскільки довжина щілин набагато більша за довжину хвилі, то дифракція вздовж щілин відсутня.
Розглянемо дифракцію Фраунгофера від двох щілин. Щілиною називають прямокутний отвір, шириною якого, порівняно з його довжиною, можна знехтувати. Нехай світлова хвиля, довжина якої λ, поширюється перпендикулярно до щілини, ширина якої а. Паралельний пучок світла, пройшовши крізь щілини, дифрагує під різними кутами φ від початкового напрямку (рис. 69.1). За щілинами розміщена лінза L, у фокальній площині якої знаходиться екран Е. На екрані спостерігається дифракційна картина – почергово розміщені світлі і темні смуги. Оскільки довжина щілин набагато більша за довжину хвилі, то дифракція вздовж щілин відсутня.
 На відміну від дифракції від однієї щілини, в даному випадку ситуація ускладнюється тим, що крім дифракції від кожної щілини, відбувається ще додавання коливань у світлових пучках, які попадають у фокальну площину лінзи L від різних щілин. В даному випадку, якщо щілин є дві, то і інтерферуватимуть два пучки. Виберемо пучки, які поширюються під однаковим кутом φ до нормалі площини, в якій лежать щілини. Тоді амплітуда коливань у цих пучках однакова (за даного кута φ). Різниця ходу Δ між променями від двох щілин, як видно з рисунка 69.1, дорівнює:
На відміну від дифракції від однієї щілини, в даному випадку ситуація ускладнюється тим, що крім дифракції від кожної щілини, відбувається ще додавання коливань у світлових пучках, які попадають у фокальну площину лінзи L від різних щілин. В даному випадку, якщо щілин є дві, то і інтерферуватимуть два пучки. Виберемо пучки, які поширюються під однаковим кутом φ до нормалі площини, в якій лежать щілини. Тоді амплітуда коливань у цих пучках однакова (за даного кута φ). Різниця ходу Δ між променями від двох щілин, як видно з рисунка 69.1, дорівнює:
 . (69.1)
. (69.1)
Цій різниці ходу відповідає однакова різниця фаз δ між сусідніми пучками:

 . (69.2)
. (69.2)
В результаті інтерференції коливань у фокальній площині лінзи утвориться результуюче коливання з деякою амплітудою А, значення якої буде залежати від різниці фаз δ, а отже і від кута дифракції φ.
На рисунку 69.2 зображено тільки три напрямки, вздовж яких поширюються промені, пройшовши дві щілини. У дійсності цих напрямків необмежена кількість. Внаслідок інтерференції на екрані спостерігаються світлі і темні смуги. Наприклад, в точці, де сходяться промені 2,2 – світла смуга (різниця ходу дорівнює 0). В міру віддалення в обидві сторони від цієї точки, різниця ходу збільшуватиметься і для точок, для яких різниця ходу буде рівна  – темна смуга, потім за різниці ходу
– темна смуга, потім за різниці ходу  – знову світла смуга і т.д. Крім того, внаслідок взаємної інтерференції світлових променів, що йдуть від двох щілин будуть виникати додаткові мінімуми (в деяких напрямках промені гасять один одного).
– знову світла смуга і т.д. Крім того, внаслідок взаємної інтерференції світлових променів, що йдуть від двох щілин будуть виникати додаткові мінімуми (в деяких напрямках промені гасять один одного).
Таким чином, положення максимумів інтенсивності, які називають головними, визначається за формулою
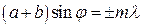 , (69.3)
, (69.3)
де m = 0, 1, 2, … . Умова додаткових мінімумів має вигляд:
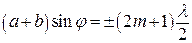 . (69.4)
. (69.4)
Зі збільшенням m інтенсивність дифракційних максимумів зменшується, а зі збільшенням кількості щілин утворюється більше додаткових мінімумів між головними максимумами.
Таблиця 69.1 –Варіанти завдань
| Номер варіанту | ||||||||||
| Довжина хвилі, нм |
Читайте також:
- I. Формула спеціальності
- I. Формула спеціальності
- I. Формула спеціальності
- Абсолютні й відносні посилання у формулах
- Барометрическая формула. Распределение
- Барометрична формула
- Барометрична формула. Больцманівський розподіл молекул в
- Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі
- Властивості товару „робоча сила”.
- Вступне звернення і заключна формула ввічливості
- Втрати енергії вздовж круглого трубопроводу. Формула Пуазейля і коефіцієнт Дарсі.
- Грування, тобто має місце формула
| <== попередня сторінка | | | наступна сторінка ==> |
| Теоретичні відомості | | | Завдання 1. Ознайомлення з роботою комп’ютерної програми та явищем дифракції від щілини |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |