
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 11. Базові комбінаційні вузли цифрових автоматів
11.1. Синтез схем у базисах І-НІ і АБО-НЕ
11.2. Синтез схем з урахуванням обмежень базису
11.1. Синтез схем у базисах І-НІ і АБО-НЕ
Під комбінаційною схемою розуміється деяка мережа логічних елементів, в якій немає зворотних зв'язків. Комбінаційна схема (КС) задається системою булевих функцій Y = F (X), в якій 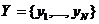 ,
,  ,
, 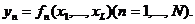
У обчислювальній техніці для синтезу КС використовується кінцева множина логічних елементів, зване елементних базисом. Це поняття пов'язане з поняттям функціонального базису, під яким розуміється кінцеве число елементарних булевих функцій, достатніх для аналітичного подання довільної булевої функції.
Так як будь-яка функція може бути представлена у вигляді ДНФ або КНФ, то очевидно, що для представлення довільних булевих функцій достатньо тільки елементарних функцій І, АБО, НЕ. Базис {І, АБО, НЕ} отримав назву булевого базису. Таким чином, для реалізації будь-якої КС достатньо елементів І, АБО і НЕ. Будь-яку ДНФ або КНФ можна виразити за допомогою операцій І-НЕ або АБО-НЕ, використовуючи закони Де Моргана:
 , (11.1)
, (11.1)
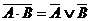 . (11.2)
. (11.2)
Таким чином, базис І-НЕ (АБО-НЕ) є достатнім для реалізації довільної функції, що й було показано раніше.
На практиці найбільш часто використовуються базиси І-НЕ і АБО-НЕ. Розглянемо методи реалізації комбінаційних схем у цих базисах.
1. Реалізація елементарної кон'юнкції в базисі І-НЕ.
Реалізація схеми ґрунтується на законі подвійний інверсії  . Наприклад, функція
. Наприклад, функція 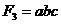 перетворюється до виду
перетворюється до виду 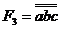 , чому відповідає комбінаційна схема (рис. 11.1). Ця схема має два рівні вентилів, причому вентиль другого рівня реалізує функцію інверсії, для чого використовується очевидне співвідношення
, чому відповідає комбінаційна схема (рис. 11.1). Ця схема має два рівні вентилів, причому вентиль другого рівня реалізує функцію інверсії, для чого використовується очевидне співвідношення
 (11.3)
(11.3)
Рис. 11.1. Реалізація елементарної кон'юнкції в базисі І-НЕ
Відзначимо, що для реалізації інвертора може бути використано і наступне правило
 . (11.4)
. (11.4)
2. Реалізація елементарної диз'юнкції в базисі І-НЕ.
Реалізація схеми заснована на одночасному використанні закону подвійного заперечення і одного із законів Де Моргана. Наприклад, функція  перетворюється наступним чином
перетворюється наступним чином  Якщо джерело вхідних змінних формує як прямі, так і інверсні значення змінного а, b, с, то схема для
Якщо джерело вхідних змінних формує як прямі, так і інверсні значення змінного а, b, с, то схема для  буде мати тільки один рівень (рис. 11.2 а). Якщо джерело вхідних сигналів формує тільки прямі значення змінних а, b, с, то схема має два рівні (рис. 11.2,б).
буде мати тільки один рівень (рис. 11.2 а). Якщо джерело вхідних сигналів формує тільки прямі значення змінних а, b, с, то схема має два рівні (рис. 11.2,б).

Рис. 11.2. Реалізація елементарної диз'юнкції в базисі І-НЕ
Відмітимо, що друга ситуація є найбільш поширеною на практиці, де джерелами інформації є виходи регістрів.
3. Реалізація ДНФ в базисі І-НЕ.
Реалізація схеми заснована на одночасному застосуванні закону подвійного заперечення і закону Де Моргана (11.1). Наприклад, для функції 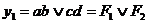 маємо:
маємо:  що відповідає схемі на рис. 4.3.
що відповідає схемі на рис. 4.3.

Рис.11.3. Реалізація ДНФ в базисі І-НЕ
4. Реалізація КНФ в базисі І-НЕ.
Так як термами КНФ є елементарні диз'юнкції, то кожна з них повинна бути перетворена за правилами, розглянутим у пункті 2. При цьому до КНФ в цілому необхідно застосувати закон подвійний інверсії. Наприклад, для булевої функції 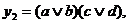 що залежить від чотирьох змінних, маємо
що залежить від чотирьох змінних, маємо 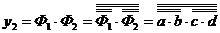 , що відповідає схемі на рис. 11.4.
, що відповідає схемі на рис. 11.4.

Рис. 11.4. Реалізація КНФ в базисі І-НЕ
Кожний логічний елемент має деякий кінцевий час 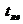 , який проходить від зміни сигналів на входах до зміни сигналів на його виході. Назвемо
, який проходить від зміни сигналів на входах до зміни сигналів на його виході. Назвемо 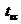 часом перемикання логічного елемента. Комбінаційна схема в цілому також володіє часом перемикання
часом перемикання логічного елемента. Комбінаційна схема в цілому також володіє часом перемикання 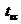 , яке знаходиться як сума часів перемикання логічних елементів, що знаходяться на самому довгому ланцюжку від входу до виходу. Так, для функції
, яке знаходиться як сума часів перемикання логічних елементів, що знаходяться на самому довгому ланцюжку від входу до виходу. Так, для функції 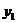 маємо
маємо 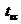 = 2, а для
= 2, а для 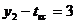 . Таким чином, для даного конкретного випадку функції
. Таким чином, для даного конкретного випадку функції  схема в базисі І-НЕ, побудована за ДНФ, в 1,5 рази швидше, ніж схема, яка за КНФ.
схема в базисі І-НЕ, побудована за ДНФ, в 1,5 рази швидше, ніж схема, яка за КНФ.
При синтезі комбінаційних схем розробник може користуватися наступними критеріями:
- мінімізація числа елементів схеми і, отже, її вартості в грошовому еквіваленті;
- мінімізація часу перемикання КС.
У разі використання другого критерію, реалізація КНФ в базисі І-НЕ не використовується. Однак може використовуватися реалізація схеми по КНФ зворотної функції. Наприклад, для функції  (рис. 11.5) може бути отримана КНФ для зворотнього функції
(рис. 11.5) може бути отримана КНФ для зворотнього функції  , яка використовує мінтерми, відповідні одиницям карти Карно.
, яка використовує мінтерми, відповідні одиницям карти Карно.

Рис. 11.5. Карта Карно для функції 
З цієї карти Карно маємо формулу  . Очевидно, для отримання прямої функції достатньо взяти інверсію функції
. Очевидно, для отримання прямої функції достатньо взяти інверсію функції  , а для реалізації термів в базисі І-НЕ необхідно використовувати подвійну інверсію і закон Де Моргана:
, а для реалізації термів в базисі І-НЕ необхідно використовувати подвійну інверсію і закон Де Моргана: 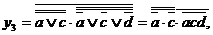 що призводить до схеми (рис. 11.6), що має два рівні.
що призводить до схеми (рис. 11.6), що має два рівні.

Рис. 11.6. Реалізація КНФ зворотної функції в базисі І-НЕ
Ця схема має такий же час перемикання, як і логічна схема, реалізована за ДНФ.
5. Реалізація елементарної кон'юнкції в базисі АБО-НЕ.
Для синтезу схеми необхідно використовувати закон подвійний інверсії і закон Де Моргана. Наприклад, для кон'юнктивного терма 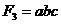 маємо
маємо  , що породжує схему (рис. 11.7).
, що породжує схему (рис. 11.7).
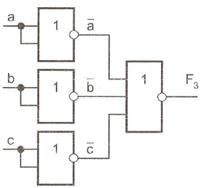
Рис. 11.7. Реалізація елементарної кон'юнкції в базисі АБО-НЕ
Б цій схемі для реалізації інверторів використано правило  . Очевидно, що в цій формулі може бути використаний і логічний нуль.
. Очевидно, що в цій формулі може бути використаний і логічний нуль.
6. Реалізація елементарної диз'юнкції в базисі АБО-НЕ.
Для реалізації терма необхідно використовувати правило подвійної диз'юнкції. Так, для вираження 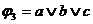 маємо
маємо 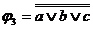 , що породжує схему (рис. 11.8).
, що породжує схему (рис. 11.8).
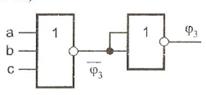
Рис. 4.8. Реалізація елементарної диз'юнкції в базисі АБО-НЕ
7. Реалізація ДНФ в базисі АБО-НЕ.
Застосовуваний підхід аналогічний методу реалізації КНФ в базисі І-НЕ: над кожним термо і над формулою в цілому береться подвійна інверсія, а потім внутрішня інверсія для кожного терма перетвориться за законом Де Моргана. Так, для деякої булевої функції  маємо:
маємо: 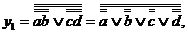 що породжує схему (рис. 11.9).
що породжує схему (рис. 11.9).

Рис. 11.9. Реалізація ДНФ в базисі АБО-НЕ
Очевидно, що така схема буде повільною і більш переважно використовувати ДНФ зворотної функції. Так, з карти Карпо (рис. 11.5) маємо ДНФ
 Отже, маємо
Отже, маємо  що породжує схему (рис. 11.10). Як видно з формули, схема повинна включати чотири елементи, що підтверджується і малюнком.
що породжує схему (рис. 11.10). Як видно з формули, схема повинна включати чотири елементи, що підтверджується і малюнком.
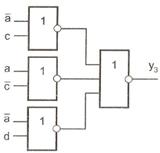
Рис. 11.10. Реалізація ДНФ зворотної функції в базисі АБО-НЕ
8. Реалізація КНФ в базисі АБО-НЕ.
Реалізація заснована на застосуванні законів подвійного заперечення Де Моргана. Так, для деякої функції  маємо:
маємо:
 , що породжує схему (рис. 11.11)
, що породжує схему (рис. 11.11)

Рис. 11.11. Реалізація КНФ в базисі АБО-НЕ
Результати, наведені в цьому параграфі, зведені в табл. 11.1
11.2. Синтез схем з урахуванням обмежень базису
Випускаються серійно елементи мають два важливих технологічних обмеження, що впливають на кількість елементів і швидкодію одержуваних на їх основі комбінаційних схем. Це наступні обмеження:
1. Число входів S логічного елемента не перевищує восьми.
2. Навантажувальна здатність 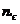 не перевищує десяти.
не перевищує десяти.
Нагадаємо, що навантажувальна здатність логічного елемента визначає кількість входів, які можуть бути пов'язані з виходом даного елемента. Це пов'язано з тим, що логічний елемент характеризується кінцевим значенням струму, який може бути отриманий з його виходу. У теж час підключені до нього елементи також вимагають деякого значення струму для правильної роботи. Розглянемо вплив параметра S, прийнявши, що нормальна форма функції містить Н термів і h-й терм містить  букв.
букв.
Таблиця 11.1
| № | Функція | Базис | Реалізація |
| 1. | 
| І-НЕ | 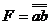
|
| АБО-НЕ | 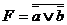
| ||
| 4. | 
| І-НЕ | 
|
| АБО-НЕ | 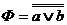
| ||
| 3. | 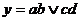
| І-НЕ | 
|
| АБО-НЕ | 
| ||
| 4. | 
| І-НЕ | 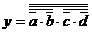
|
| АБО-НЕ | 
|
1. Реалізація елементарної кон'юнкції в базисі І-НЕ.
Існує три області, які визначаються поєднанням параметрів  ; і S:
; і S:  = 1;
= 1;
1 <  ≤S ;
≤S ;  > S. Розглянемо особливості реалізації термів в цих областях, прийнявши для визначеності S = 4.
> S. Розглянемо особливості реалізації термів в цих областях, прийнявши для визначеності S = 4.
a).  =1.
=1.
Розглянемо терм 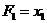 . Цей терм відповідає, як диз'юнкції, так і кон'юнкції. Очевидно, що для реалізації схеми, відповідної терму
. Цей терм відповідає, як диз'юнкції, так і кон'юнкції. Очевидно, що для реалізації схеми, відповідної терму  , жодних логічних елементів не потрібно. У цьому випадку схема являє собою просто провідник (рис. 11.12 а). У практичних випадках може виникнути необхідність у дублюванні змінної.
, жодних логічних елементів не потрібно. У цьому випадку схема являє собою просто провідник (рис. 11.12 а). У практичних випадках може виникнути необхідність у дублюванні змінної.
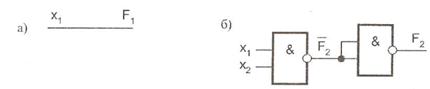
Рис. 11.12. Реалізація кон'юнкцій  при
при  =1 (a) і
=1 (a) і  = 2 (б)
= 2 (б)
б).  = 2 ≤S.
= 2 ≤S.
Реалізація схеми ґрунтується на використанні законів подвійної інверсії (  ) і ідемпотентності (
) і ідемпотентності (  ). Так, для терма
). Так, для терма 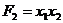 маємо
маємо 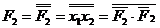 , що відповідає схемі на рис. 11.12,б.
, що відповідає схемі на рис. 11.12,б.
в).  = 3> S.
= 3> S.
Якщо  > S, то для реалізації схеми використовується метод розбиття терма на підтерми, що включає наступні етапи:
> S, то для реалізації схеми використовується метод розбиття терма на підтерми, що включає наступні етапи:
1. Розбити терм 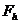 , на 5 підтермів
, на 5 підтермів  з приблизно однаковим числом літер.
з приблизно однаковим числом літер.
2. Якщо підтерм  містить одну букву, то перетворення підтерма
містить одну букву, то перетворення підтерма 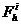 завершено.
завершено.
3. Якщо підтерм 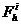 (
( 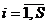 ) містить не більш S букв, то до нього застосовується операція подвійної інверсії і на цьому перетворення підтерма
) містить не більш S букв, то до нього застосовується операція подвійної інверсії і на цьому перетворення підтерма 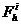 закінчується.
закінчується.
4. Якщо підтерм 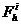 (
( 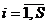 ) містить більш S букв, то до підтерма застосовуються операції подвійної інверсії і знаходиться розбиття підтерма на S
) містить більш S букв, то до підтерма застосовуються операції подвійної інверсії і знаходиться розбиття підтерма на S
підтермів  з приблизно однаковим числом літер.
з приблизно однаковим числом літер.
5. Пункти 2-4 виконуються циклічно до тих пір, поки всі одержані підтерми не будуть містити не більше S букв.
6. Перетворені підтерми збираються в єдиний терм. Розбиття на приблизно однакову кількість літер необхідно для отримання схеми з максимально можливим швидкодією, як буде показано далі. Поки що можна зазначити, що рівномірне розбиття термів призводить до схем з мінімально можливим числом логічних рівнів. При цьому мінімізується загальна затримка поширення сигналу в схемі.
Розглянемо застосування цього методу до терму 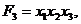 при цьому будемо позначати підтерми літерами латинського алфавіту для більшої ясності викладу.
при цьому будемо позначати підтерми літерами латинського алфавіту для більшої ясності викладу.
1. Терм 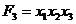 розбивається на S = 2 частини а =
розбивається на S = 2 частини а = 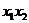 , b -
, b -  .
.
2. Підтерм а містить дві букви, перетворення полягає в подвійній інверсії а= 
3. Підтерм b містить одну букву і не вимагає перетворення.
4. Після виконання п.6 методу маємо: 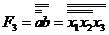 , що відповідає схемі на рис. 11.13.
, що відповідає схемі на рис. 11.13.

Рис.11.13. Реалізація кон'юнкції 
Розглянемо більш складний приклад, коли необхідно реалізувати терм 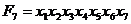 на елементах І-НЕ з двома входами (2І-НЕ). 1. Розіб'ємо
на елементах І-НЕ з двома входами (2І-НЕ). 1. Розіб'ємо  на дві частини
на дві частини  , де
, де  ,
, 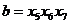 .
.
2. Перетворимо частину а до виду  і розіб'ємо на дві частини
і розіб'ємо на дві частини  і
і 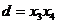 :
:  .
.
3. Розіб'ємо  на дві частини
на дві частини 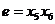 і
і 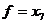 :
: 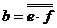 .
.
4. Перетворимо c:c=  - перетворення c закінчено.
- перетворення c закінчено.
5. Перетворимо d:d=  - перетворення d закінчено. Тепер маємо:
- перетворення d закінчено. Тепер маємо:  .
.
6. Перетворимо е:е=  - перетворення е закінчені. Так як терм f не вимагає перетворень, тому маємо
- перетворення е закінчені. Так як терм f не вимагає перетворень, тому маємо  .
.
7. Тепер формуємо терм  отримаємо вираз
отримаємо вираз  , що відповідає схемі (рис. 11.14).
, що відповідає схемі (рис. 11.14).
Процес розбиття терма  на підтерми і синтезу схеми показаний графом на рис. 11.15, де знаком * - відзначений момент закінчення перетворення підтерма і початку побудови схеми.
на підтерми і синтезу схеми показаний графом на рис. 11.15, де знаком * - відзначений момент закінчення перетворення підтерма і початку побудови схеми.

Рис. 11.14. Реалізація кон'юнкції  на елементах 2І-НЕ
на елементах 2І-НЕ
Застосування розглянутого методу до терму з  літерами при використанні елементів з S входами завжди призводить до схем, що мають n (
літерами при використанні елементів з S входами завжди призводить до схем, що мають n (  , S) A логічних елементів, де
, S) A логічних елементів, де
 (11.5)
(11.5)
Тут [а] означає найближче ціле число, більше, ніж число а, якщо а - дробове число, або рівне а, якщо а - ціле число.
Застосування (11.5) при  = 7, S= 2 дає n(7,2)=12, що відповідає схемі на рис. 11.14. Відзначимо, що кількість вентилів n(
= 7, S= 2 дає n(7,2)=12, що відповідає схемі на рис. 11.14. Відзначимо, що кількість вентилів n(  , S) не залежить від способу розбиття терма
, S) не залежить від способу розбиття терма  на підтерми. Модифікуємо розглянутий метод так, щоб один з підтермів завжди складався з однієї літери. Тоді перетворення терма
на підтерми. Модифікуємо розглянутий метод так, щоб один з підтермів завжди складався з однієї літери. Тоді перетворення терма  породжує наступну формулу
породжує наступну формулу 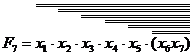 , що призводить до схеми (рис. 11.16).
, що призводить до схеми (рис. 11.16).
Назвемо схемою С1 (С2) реалізацію терма на рис. 11.14 (11.16) і проаналізуємо ці схеми. Обидві схеми С1 і С2 мають однакове число вентилів n(  , S) = 14.
, S) = 14.
Відзначимо, що 14 дорівнює числу інверсій, які об'єднують більше однієї літери формули. На самому довгому шляху від вхідних змінних до вихідних в схемі С1 знаходиться n(С1) = 6 вентилів, а n(С2) = 12 вентилів.
Таким чином, час перемикання схеми C1 t(C1) = n (C1) 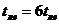 , а t (С2) = 12
, а t (С2) = 12  . Отже, при однакових апаратурних витратах схема С1 в два рази швидша, ніж схема С2. Так як при проектуванні цифрових пристроїв прагнуть до отримання схем з максимально можливим швидкодією, то схема С1 є найбільш кращою з усіх можливих реалізацій при S=2.
. Отже, при однакових апаратурних витратах схема С1 в два рази швидша, ніж схема С2. Так як при проектуванні цифрових пристроїв прагнуть до отримання схем з максимально можливим швидкодією, то схема С1 є найбільш кращою з усіх можливих реалізацій при S=2.
Оскільки спосіб розбиття терма на підтерми призводить до схем з різним швидкодією, то в розглянутому методі використовується розбиття на підтерми з приблизно однаковим числом літер. Як видно з порівняння схем С1 і С2, такий підхід дозволяє оптимізувати швидкодію комбінаційної схеми.

Рис. 11.15 Графічне зображення процесу перетворення терма  і синтезу схеми на елементах 2І-НЕ.
і синтезу схеми на елементах 2І-НЕ.

Рис. 11.16. Нераціональна реалізація терма  в базисі 2І-НЕ
в базисі 2І-НЕ
2. Реалізація ДНФ в базисі І-НЕ.
В цьому випадку до ДНФ застосовується подвійне заперечення і закон Де Моргана. Так, для деякої булевої функції дванадцяти змінних  маємо формулу:
маємо формулу:  . Отже, логічне вираз є кон'юнкція, отже, реалізація комбінаційної схеми зводиться до послідовного перетворення кожного терма
. Отже, логічне вираз є кон'юнкція, отже, реалізація комбінаційної схеми зводиться до послідовного перетворення кожного терма  і формули в цілому по розглянутому раніше методом. Так як кожен з елементів формули входить до неї з інверсією, то на першому етапі перетворення відпадає необхідність в подвійній інверсії.
і формули в цілому по розглянутому раніше методом. Так як кожен з елементів формули входить до неї з інверсією, то на першому етапі перетворення відпадає необхідність в подвійній інверсії.
Розглянемо приклад застосування розглянутого методу. Так, для перетворення формули для 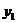 потрібно шість кроків. Розглянемо процес перетворення ДНФ
потрібно шість кроків. Розглянемо процес перетворення ДНФ 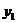 без докладних коментарів (S=2):
без докладних коментарів (S=2):
а). 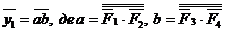 .
.
б).  .
.
в). 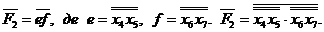 .
.
г). 
д) 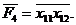
e). Отже, 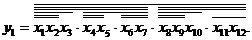
Отримане вираження для 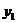 відповідає схемі (рис.11.17). Визначимо формулу для підрахунку кількості елементів у комбінаційної схемою. Так як кожен терм реалізується в інверсної формі, то для його реалізації необхідно
відповідає схемі (рис.11.17). Визначимо формулу для підрахунку кількості елементів у комбінаційної схемою. Так як кожен терм реалізується в інверсної формі, то для його реалізації необхідно  вентилів. Для функції, що має Н термів, необхідно
вентилів. Для функції, що має Н термів, необхідно  вентилів. Таким чином, для реалізації ДНФ функції у з Н термами
вентилів. Таким чином, для реалізації ДНФ функції у з Н термами  кожен з яких має
кожен з яких має  букв, де
букв, де  ≤L, потрібно
≤L, потрібно  вентилів:
вентилів:
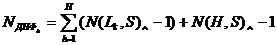 (11.7)
(11.7)
Використовуючи (11.6) і (11.7), отримаємо шукану формулу.
 (11.8)
(11.8)

Рис. 11.17. Реалізація функції 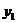 в базисі 2І-НЕ
в базисі 2І-НЕ
Так, для функції 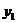 маємо:
маємо:

що відповідає числу вентилів у схемі СЗ (рис. 11.17). Для схеми СЗ маємо n(СЗ) = 6, тобто t(C3)=6 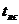 . Відзначимо, що це число збігається з максимальним числом заперечень, загальних більше, ніж для однієї літери перетвореної формули для
. Відзначимо, що це число збігається з максимальним числом заперечень, загальних більше, ніж для однієї літери перетвореної формули для 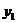 . Формула (11.8) може бути використана для попередньої оцінки числа вентилів у схемі. Це дозволяє визначити складність схеми без її реалізації.
. Формула (11.8) може бути використана для попередньої оцінки числа вентилів у схемі. Це дозволяє визначити складність схеми без її реалізації.
3. Реалізація елементарної диз'юнкції в базисі І-НЕ.
Реалізація схеми заснована на використанні законів подвійної інверсії і Де Моргана, а також на застосуванні розглянутого методу перетворення кон'юнкції.
Наприклад, для терма  маємо
маємо 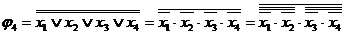 , що призводить до схеми на рис. 11.18.
, що призводить до схеми на рис. 11.18.
Якщо в схемі немає джерел, які формують як прямі, так і інверсні значення сигналів, то для реалізації схеми необхідно  вентилів, формують заперечення вхідних сигналів. Таким чином, для реалізації диз'юнкції необхідна наступна кількість вентилів з заданими обмеженнями:
вентилів, формують заперечення вхідних сигналів. Таким чином, для реалізації диз'юнкції необхідна наступна кількість вентилів з заданими обмеженнями:
 (11.9)
(11.9)
Знак 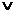 у формулі (11.9) підкреслює, що в основі формули знаходиться диз'юнкція. Так, для
у формулі (11.9) підкреслює, що в основі формули знаходиться диз'юнкція. Так, для 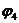 маємо
маємо 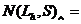 9 логічних елементів, що відповідає схемі на рис. 11.18.
9 логічних елементів, що відповідає схемі на рис. 11.18.

Pиc. 11.18. Реалізація диз'юнкції 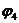 в базисі 2І-НЕ
в базисі 2І-НЕ
4. Реалізація КНФ в базисі І-НЕ.
Реалізація схеми заснована на застосуванні законів подвійної інверсії до кожного терму  , і КНФ в цілому, а так само, на застосуванні закону Де Моргана до кожного терму функції. Наприклад, для булевої функції
, і КНФ в цілому, а так само, на застосуванні закону Де Моргана до кожного терму функції. Наприклад, для булевої функції 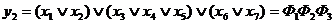 можна отримати формулу:
можна отримати формулу:
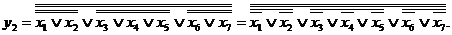
Хід подальшого перетворення зводиться до перетворення кожного терма і функції в
цілому. Для функції  , маємо
, маємо  , що призводить до схеми (мал. 11.19), де інвертори, використовувані для формування сигналів
, що призводить до схеми (мал. 11.19), де інвертори, використовувані для формування сигналів 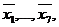 не показані. Принцип побудови цієї комбінаційної схеми очевидний. Схема починається від самих внутрішніх кон'юнкцій, а потім відбувається підйом по формулі, як по деякому дереву.
не показані. Принцип побудови цієї комбінаційної схеми очевидний. Схема починається від самих внутрішніх кон'юнкцій, а потім відбувається підйом по формулі, як по деякому дереву.
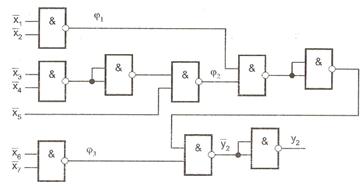
Рис. 11.19. Реалізація КНФ  в базисі 2І-НЕ
в базисі 2І-НЕ
Для реалізації кожного терма  , потрібно
, потрібно  елементів, для реалізації кон'юнкції
елементів, для реалізації кон'юнкції  необхідно
необхідно  логічних елементів, для реалізації інверсних значень входів необхідно L логічних елементів. Отже, для реалізації КНФ необхідно
логічних елементів, для реалізації інверсних значень входів необхідно L логічних елементів. Отже, для реалізації КНФ необхідно
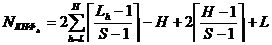 (11.10)
(11.10)
логічних елементів І-НЕ з S входами. Так для КНФ  при S = 2 маємо
при S = 2 маємо  що відповідає рис. 11.19 з урахуванням L = l інверторів для вхідних сигналів.
що відповідає рис. 11.19 з урахуванням L = l інверторів для вхідних сигналів.
Число рівнів схеми може бути зменшена за рахунок використання КНФ зворотної функції. Нагадаємо, що зворотна функція вже несе в собі внутрішню інверсію. Число вентилів у цьому випадку визначається наступним виразом:

5. Реалізація схем у базисі АБО-НЕ
Методи синтезу схем у базисі АБО-НЕ аналогічні методам синтезу в базисі І-НЕ. При цьому диз'юнкція  , реалізується також як кон'юнкція
, реалізується також як кон'юнкція  в базисі І-НЕ, КНФ як ДНФ,
в базисі І-НЕ, КНФ як ДНФ,  як
як  , ДНФ як КНФ. Розглянемо, наприклад, реалізацію комбінаційної схеми для функції, заданої КНФ
, ДНФ як КНФ. Розглянемо, наприклад, реалізацію комбінаційної схеми для функції, заданої КНФ 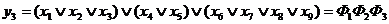 , в базисі 2АБО-НЕ:
, в базисі 2АБО-НЕ:
а).  ;
;
б). 
в). 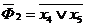 ;
;
г). 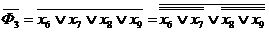 ;
;
д).  ;
;
У результаті проведених перетворень будується схема (рис. 11.20).
У таблиці 11.2 наведені формули, які дозволяють визначити число елементів в комбінаційних схемах, що реалізовуються в різних базисах.
Розглянемо вплив фактора навантажувальної здатності на кінцевий вигляд комбінаційної схеми. Якщо число вентилів, пов'язаних з виходом логічного елемента, перевищує  , то використовуються два основних способи підвищення навантажувальної здатності:
, то використовуються два основних способи підвищення навантажувальної здатності:
1. Дублювання виходу вентиля.
2. Дублювання вентиля.

Рис. 11.20. Реалізація КНФ  в базисі 2АБО-НЕ
в базисі 2АБО-НЕ
Наприклад, вентиль І-НЕ має  = 3, а терм
= 3, а терм  входить до ДНФ п'яти функцій, тобто до виходу вентиля підключені входи п'яти вентилів (
входить до ДНФ п'яти функцій, тобто до виходу вентиля підключені входи п'яти вентилів (  = 5). Метод дублювання виходу вентиля породжує схему (рис. 11.21 а), а метод дублювання вентиля дає наступну схему (рис. 11.21 б).
= 5). Метод дублювання виходу вентиля породжує схему (рис. 11.21 а), а метод дублювання вентиля дає наступну схему (рис. 11.21 б).
Перший з цих методів зменшує швидкодію комбінаційної схеми за рахунок збільшення числа рівнів. Другий метод дозволяє зберегти швидкодію, але підвищує вимоги до характеристик вхідних сигналів a і b, навантажувальна здатність яких також кінцева.
Розглянуті в цьому параграфі методи синтезу комбінаційних схем можна назвати методами "розкладання, інвертування і з'єднання", що відображає процес синтезу КС з урахуванням обмежень елементного базису. Методи синтезу КС у базисах І-НЕ і АБО-НЕ аналогічні, тому надалі будемо розглядати тільки базис І-НЕ.
Таблиця 11.2
Визначення числа елементів комбінаційних схем
| № | Функція | Базис | Число элементів в схемі |

| І-НЕ | 
| |

| АБО-НЕ | ||

| АБО-НЕ | 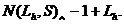 N(Lh,S)-\ + Lh N(Lh,S)-\ + Lh
| |

| І-НЕ | ||
| ДНФ у | І-НЕ | 
| |
| КНФ у | АБО-НЕ | ||
| ДНФ у | АБО-НЕ | 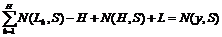
| |
| КНФ у | І-НЕ | ||
| ДНФ у | АБО-НЕ | 
| |
| КНФ у | І-НЕ |
Читайте також:
- II. Множення круглих багатоцифрових чисел на розрядні числа.
- Автомобільні ваги із застосуванням цифрових датчиків
- Базові (головні, стратегічні) психологічні проблеми управління.
- Базові (ключові) цінності.
- Базові елементи управління проектом
- Базові емоції
- Базові засади менеджменту
- БАЗОВІ ЗАСАДИ СТВОРЕННЯ ОРГАНІЗАЦІЙНОЇ СТРУКТУРИ ПРОЕКТУ
- Базові знання, вміння, навички, необхідні для вивчення теми
- Базові знання, вміння, навички, необхідні для вивчення теми (міждисциплінарна інтеграція)
- Базові знання, вміння, навички, необхідні для вивчення теми (міждисциплінарна інтеграція)
- Базові і основні деталі агрегатів автомобіля
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 10. Логічні елементи та їх класифікація | | | Тема 12. Синтез дешифраторів та шифраторів |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |