• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Зразок варіанта тестового завдання по ЗМ 1.

Варіант 1

1) Доведіть тотожність, використовуючи похідну:

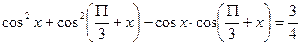.(4 бали)

2) Доведіть нерівність, використовуючи похідну: 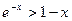, при 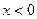. (4 бали)

3) Розв’яжіть рівняння методом оцінки, використовуючи похідну: 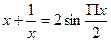. (4 бали)

4) У півколо радіуса 20 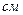вписано прямокутник найбільшої площі. Знайдіть сторони прямокутника. (4 бали)

Опрацювання ЗМ 2 та ЗМ 3 відбуватиметься на практичних заняттях(березень – червень 2015 року) + САМОСТІЙНА РОБОТАз виконання КЗСР,умови завдань запропоновані далі.

Комплекс завдань самостійної роботи з ПРЗ по ЗМ2 ”Методи і способи розв’язування

планіметричних задач на обчислення, доведення, побудову”

Частина 1. Методи і способи розв’язування планіметричних задач на обчислення.

1) (Метод ключових задач).

Довжина середньої лінії трапеції дорівнює 5, а довжина відрізка, який з’єднує середини основ, - 3. Кути при більшій основі дорівнюють 30 і 60 . Знайдіть основи трапеції і її площу.

Вказівка. Через середину верхньої основи проведіть прямі паралельні до бічних сторін.

2) (Метод ключових задач).

Медіану, яка виходить із вершини 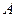трикутника , продовжено до перетину в точці 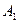з описаним колом. Знайти довжину , якщо медіана дорівнює 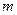, а сторона .

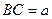3) (Метод площ).

У трикутнику дано: 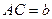, , 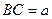, 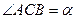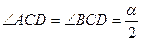. Знайти довжину .

4) (Метод допоміжної площі).

У трикутнику довжини двох сторін дорівнюють 6 і 3. Знайти довжину третьої сторони, якщо пів сума висот, проведених до даних сторін, дорівнює третій висоті.

5) (Метод допоміжного відрізка).

Основи трапеці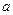ї - і 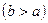. Знайти довжину відрізка, паралельного основам, який поділяє площу трапеції навпіл.

6) (Метод допоміжного кута).

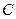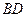В прямокутному трикутнику з вершини прямого кута опущено висоту . Проекція відрізка на катет 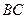дорівнює 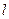, а проекція відрізка 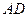на катет 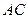дорівнює 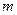. Знайти довжину гіпотенузи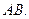

7) (Метод координат).

На площині дано дві точки 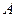і 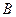. Точка 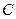переміщується в площині так, що медіана 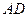трикутника залишається незмінною. Знайти множину точок .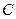

8) (Метод векторів).

У трикутнику бісектриса 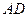ділить сторону 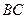у відношенні 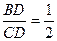. В якому відношенні медіана 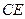ділить цю бісектрису?

Частина 2. Методи і способи розв’язування планіметричних задач на доведення.

9) (Метод ключових задач).

Довести, що для будь-якої точки 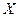кола, описаного навколо прямокутника 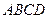, сума - величина постійна.

10) (Метод від супротивного).

Дано чотири прям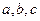і і 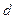. Відомо, що прямі 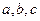перетинаються в одній точці й прямі 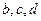також перетинаються в одній точці. Доведіть, що всі чотири прямі також проходять через одну точку.

11) (Метод повороту).

Через центр квадрата проведено дві взаємно перпендикулярні прямі. Довести, що відрізки прямих, які знаходяться в середині квадрата, однакові.

12) (Метод допоміжної площі).

Довести, що бісектриса трикутника дорівнює 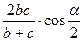, де , , .

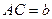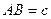13) (Метод допоміжного кола).

З точки 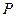, розміщеної в середині гострого кута , проведено перпендикуляри і 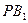відповідно на прям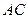і і 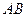. Довести, що .

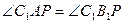14) (Метод ”подовження” медіани).

Дано прямокутник 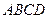. Довести, що для будь-якої точки площини .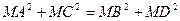

15) (Метод векторів).

Довести, що висота прямокутного трикутника, проведена з вершини прямого кута на гіпотенузу, є середнє пропорційне між проекціями катетів на гіпотенузу.

16) (Метод векторів).

Довести, що діагоналі ромба взаємно перпендикулярні.

Частина 3. Методи і способи розв’язування планіметричних задач на побудову.

17) (Метод центральної симетрії).

Дано коло, пряма і точка 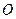. Побудувати точки, симетричні відносно точки 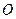, які лежали б на даних прямій і колі.

18) (Метод осьової симетрії).

Побудувати прямокутний трикутник за катетом 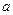і різницею 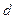двох інших сторін.

19) (Метод повороту).

Дано коло, квадрат і точка 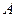. Побудувати рівнобедрений трикутник ( 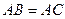), вершини 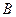і 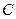якого належали б колу і стороні квадрата, а кут дорівнював би .

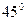20) (Метод гомотетії).

У даний трикутник вписати ромб із даним гострим кутом так, щоб одна з його сторін лежала на стороні 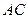трикутника, а дві інші вершини на сторонах 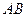і .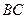

Читайте також:

1. I. Постановка завдання статистичного дослідження
2. I. ПРЕДМЕТ, МЕТА ТА ЗАВДАННЯ ДИСЦИПЛІНИ
3. II. Завдання на проект.
4. II. Перевірка домашнього завдання.
5. II. Перевірка домашнього завдання.
6. II. Перевірка домашнього завдання.
7. II. Перевірка домашнього завдання.
8. II. Перевірка домашнього завдання.
9. II. Перевірка домашнього завдання.
10. II. Перевірка домашнього завдання.
11. II. Перевірка домашнього завдання.
12. II. Перевірка домашнього завдання.

Переглядів: 618