• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Постійні та змінні величини. Властивості функцій.

Величина – це об`ект довільної природи, якому становиться у відповідність певне числове значення.

Величина буває постійною і змінною.

Змінною наз. величина, яка приймає різні числові значення(розмір зарплати, розмір стипендії, товарообіг).

Величина, числове значення, якої не змінюється наз. постійною.

Але при розгляді конкретних явищ, одна і таж величина в одному і явищі постійна, а в іншому- змінна.

Але є величини , які залишаються незмінними в любому явищі, такі величини наз.абсолютно сталими (шв.світла).

Змінні величини наз.незалежними, якщо вони змінюються в процесі, і приймають різні числові значення.

Змінна величина наз.залежною, яка приймає різні числові значення, в залежності від того, які числові значення прийняла інша величина .

Власт.функції:

1) Парні,непарні,функції.

y=f(x) парна, якщо f(-x)=f(x)

y=f(x)-непарна,якщо f(-x)=-f(x) графік парної ф-ції симетричне відносно ox, г-фік непарної симетричне поч..координат.Ф-ція,яка не має властивостей непарної, не непарної відноситься до ф-ції загального вигляду. 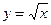функція загального вигляду.

2) зростання і спадання ф-ції

y=f(x) наз.зростаючою на інтервалі, якщо для любих Х₁,Х₂ з цього інтервалу таких щоб

Х₁<Х₂=> f(x₁)<f(x₂)-зростаюча

f(x₁) 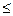f(x₂)-неспадна

y=f(x) наз.спадною на інтервалі, якщо для любих Х₁,Х₂ для цього інтервалу х₁,х₂- виконується нерівність

Х₁<Х₂=> 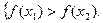- спадна

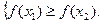- незростаюча

Функція на деякому інтервалі наз.множинними ф-ціями.

3) Ф-ція Y=f(x) наз.періодичною,якщо існує таке число Т>0, що існує

f(x)+(Т)= f(x).

4) Обмежені, необмежені ф-ції: y=f(x), х Е наз.обмеженою, якщо існує таке число М>0,що | f(x)| 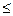M для всіх чисел де х₀ Е, що | f(x₀)|> М. Монотонні ф-ції.

1) y=f(x) наз.зростаючою,спадною, якщо для довільних х₁ Е, х₂ Е, з умови х₁< х₂ випливає f(x₁) 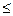f(x₂)

(f(x₁) 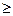f(x₂)). Зростаючі,спадні,не зростаючі,неспадні,ф-ції наз.монотонними.

35. Oгляд найпростіших елементарних функцій( на прикладі y=tgx, y= log_ax).

1. Частку від ділення функції sinx на cosx наз. Функцією tgx.

Tgx= .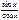

Властивості функції:

1) область визначення: 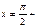pk, k Z.

2) Множина значень – уся числова пряма, тобто Е=( tgx) = R.

3) Функція непарна, тому що tg(-x)=-tgx тобто графік симетричний відносно початку координат.

4) Функція періодична з найменшим додатковим періодом Т=p,тому що tg(x+ p)= tgx

5) Точки перетину з осями координат.з віссю ОУ: х=0;у= tg0;у=0,отже,графік проходить через початок координат- т.(0,0).З віссю ОХ: tgx=0; х=pk, k 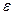Z.

6) Проміжки знакосталості: tgx>0,якщо x 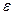(0+pk; + pk), k 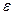Z, 1 і 3 чверть,

7) Tgx<0,якщо x 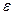( - + pk; 0+ pk), k 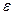Z, 2 і 4 чверті.

7)Функція неперервна в кожній точці своєї області визначкння( і на будь-якому інтервалі, що входить до обл.. визначення) та має похідну при будь-якому значенню аргументу з D(y): (tgx)` = .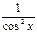

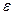8) функція зростає на кожному із проміжків ( - + pk; + pk), k Z.

9) мінімумів і максимумів немає.

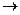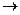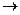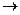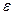10) Асимптоти. Якщо х - +0 у= tgx -¥ . якщо х - -0 у= tgx ¥. Отже, х= - і х= - вертикальні асимптоти. А оскільки функція періодична і Т=pk, то х=- + pk, k Z.

-асимптоти графіка функції.

11) графіком функції є тангенсоїда.

2. функція вигляду у=log_ax, де а>0, а¹1, наз. Логарифмічною. Для побудови графіка логарифмічної ф-ї скористаємося властивістю графіка ф-ї оберненої для даної. Графіке ф-ї у=log_ax, можна дістати з графіка показникової ф-ї, симетрично відобразивши останній відносно прямої у=х.

Властивості логарифмічної ф-ї.

1). Область визначення логарифмічної ф-ї – множина всіх додатних чисел: D(log_ax)=(0;+¥).

2). Область значення логарифмічної ф-ї – множина всіх дійсних чисел: Е(log_ax)=R.

3). Ф-я у=log_ax є зростаючою на всій області визначення, якщо а>1, якщо 0<a<1, то логарифмічна ф-я є спадною на всій області визначення.

4). Якщо у=0, тобто log_ax = 0, то х= а⁰ =1.

5). Ф-я неперервна і диференційована на всій області визначення (log_ax)` = ;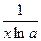

6). У>0, якщо x>1 і у<0, якщо 0<x<1, якщо а>1; у>0, якщо 0<x<1 і у<0, якщо х>0 якщо 0<a<1.

7). При х®+0 у®-¥ ( якщо а>1)

х=0 - вертикальна асимптота.

При х®+0 у®+¥ ( якщо 0<а<1)

37. границя функції при х®а, х®¥. Геометричний зміст. Основні теореми про границі. Особливі випадки розкриття невизначеностей вигляду.

Постійне число А наз. границею функції y = f(x), при х®х_0, якщо для любого досить малого додатного числа епсілон існує таке досить мале додатнє число більше 0, що для всіх х, що задовольняють умові 0< |x-x₀|<d(E)Þ |f(x)-A|< E.

Геометрично це означає, що всі члени послідовності (х_п) з номерами n>n₀(e) попадуть в інтервал (а- e ; а-+e), який назив. e-околом числа а. За межами цього інтервалу можу бути не більше n₀(e) перших членів послідовності (х_п), тобто з членів х_1,х₂,....х_п усі або окремі з них не попадуть в інтервал(а- e ; а-+e).

Число А наз. границею функції y = f(x), при х®¥,якщо для довільного дійсного числа e>0 існує таке дійсне число d(E)>а, що для всіх чисел х>d(E) виконується нерівність |f(x)-A|< E.

Геометрично це означає, що графік функції y = f(x) для всіх достатньо великих х як завгодно близько підходить до прямої у=А і знаходиться для чисел х>d(E) у смузі (А- e ; А +e).пряма у=А є горизонтальною асимптотою графіка функції y = f(x). Графіка функції y = f(x) може мати і похилі асимптоти y=kx+b,k¹0.

Основні теореми про границі:

1. якщо границя функції в т. Х₀ існує, то вона єдина.

2. границя суми скінченого числа ф-цій дорівнює сумиі границь цих ф-цій. Теорема справедлива для границі різниці функцій.

(f₁(x)+f₂(х))= f₁(x) 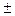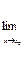f₂(х).

3. Границя добутку скінченого числа ф-ції=добутку границь цих ф-цій, при умові ,що вони існують

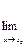(f₁(x)*f₂(х))= 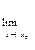f₁(x)* 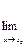f₂(х).

4.Границя константи=константі lim c=c, с=const.

5.Сталий множник можна виносити за знак границі. lim c f(x)=с lim f(x).

6.Границя частки двох ф-цій=відношенню границь при умові границя знаменника 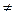0

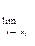
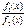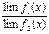
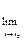= (f₂(x)≠0.

Читайте також:

1. OПТИЧНІ ВЛАСТИВОСТІ КОЛОЇДНИХ СИСТЕМ
2. А) Товар і його властивості.
3. Абсолютні, відносні та середні величини.
4. Аденогіпофіз, його гормони, механізм впливу, прояви гіпер- та гіпофункцій.
5. Аеродинамічні властивості колісної машини
6. Алкани (насичені вуглеводні). Хімічні властивості алканів
7. Алкани, їх хімічні властивості.
8. Алкени. Хімічні властивості
9. Алкіни. Хімічні властивості
10. Аміни. Фізичні та хімічні властивості аліфатичних амінів.
11. Аналізатори людини та їхні властивості.
12. Аналізатори людини та їхні властивості.

Переглядів: 2267