• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рівносильність рівнянь

Означення. Два рівняння, множини розв’язків яких на певній множині М збігаються, називаються рівносильними.

Наприклад, рівняння 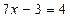і 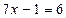рівносильні на множині R, бо множина коренів першого рівняння {1} і множина коренів другого рівняння{1},тобто множини коренів рівні.

Теорема 1. Нехай рівняння f (х) = g (x) задано на множині Х і h (х) – вираз, який визначений на тій же множині Х. Тоді рівняння 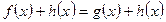і дане рівняння f (х) = g (x) рівносильні.

Доведення. Нехай Т₁ множина розв’язків рівняння (1), а Т₂ множина розв’язків рівняння (2). Покажемо, що множини коренів рівні.

Нехай число а є коренем рівняння (1). Тоді 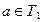і при підстановці у рівняння (1) обертає його у істинну числову рівність: f (а) = g (а), а вираз h (х) у числовий вираз 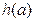. Додамо до обох частин рівності f (а) = g (а) вираз 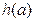. Отримаємо істинну числову рівність , а це означає, що а є коренем рівняння (2). Отже, кожен корінь рівняння (1) є коренем рівняння (2). Аналогічно можна показати, що кожен корінь 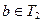рівняння (2) є коренем рівняння (1). За доведенням 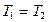і дані рівняння рівносильні.

Теорема 2. Нехай рівняння f (х) = g (x) задано на множині Х і h (х) – вираз, який визначений на тій же множині Х і який не перетворюється на нуль ні при яких значеннях х із множини Х. Тоді рівняння 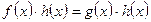і дане рівняння 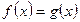рівносильні.

Доведення аналогічне до доведення першої теореми.

При розв’язуванні рівнянь частіше використовуються не самі теореми, а наслідки з них.

Наслідки з теорем про рівносильність рівнянь

До теореми 1

1. Якщо до обох частин рівняння додати одне й те саме число, то дістанемо рівняння, рівносильне даному.

2. Якщо в рівнянні перенести доданок з однієї частини в другу, змінивши його знак на протилежний, то дістанемо рівняння, рівносильне даному.

До теореми 2

3. Якщо обидві частини рівняння помножити (або поділити) на одне і те саме число, відмінне від нуля, то дістанемо рівняння, рівносильне даному.

Наприклад. Розв’язати рівняння: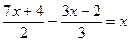

1. Зведемо до спільного знаменника вираз у лівій частині рівняння. Це тотожне перетворення виразу. Дістанемо рівняння, рівносильне даному:

;

2. Зведемо подібні доданки. Це тотожне перетворення виразу. Дістанемо рівняння, рівносильне даному:

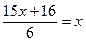
3. За наслідком (3) з теорем про рівносильність рівнянь помножимо обидві частини рівняння на 6. Дістанемо рівняння, рівносильне даному:

4. За наслідком (1) з теорем про рівносильність рівнянь перенесемо вираз 6х з правої частини рівняння в ліву, а число 16 – з лівої частини рівняння в праву, змінивши їх знаки на протилежні. Дістанемо рівняння, рівносильне даному:

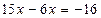
5. Зведемо подібні в лівій частині рівняння. Це тотожне перетворення, тому дістанемо рівняння, рівносильне даному:

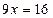
6. Поділимо ліву і праву частини рівняння на 9. За наслідком (3) дістанемо рівняння рівносильне даному.

;

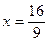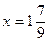
Отже, множина розв’язків рівняння складається з одного числа , тобто { }.

В початковому курсі математики розглядаються найпростіші рівняння виду: 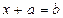; ; 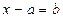; ; 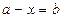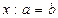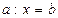, де а і b – цілі невід’ємні числа, х – змінна та рівняння на дві дії. Поняття рівняння вводиться неявно, через текст, тобто контекстуально. Розв’язуються такі рівняння в початковій школі на основі знань учнів залежностей між компонентами і результатом дій.

Наприклад. Розв’язати рівняння: 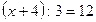. Невідоме знаходиться у діленому. Щоб знайти ділене, треба частку помножити на дільник. Дістанемо рівняння: 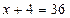. Невідомий перший доданок; щоб його знайти, треба від суми відняти другий доданок. 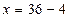; . Отже, розв’язком рівняння є число 32.

Читайте також:

1. Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
2. Визначення коефіцієнтів рівнянь лінійної регресії для багатофакторної задачі
3. Використання міждержавних порівнянь у мотивації учасників.
4. Для складання системи нормальних рівнянь
5. Довільні системи лінійних алгебраїчних рівнянь
6. Запис рівнянь чотириполюсника через вторинні параметри.
7. Застосування перетворення за Лапласом для розв’язування диференціальних рівнянь
8. Застосування рівнянь та їх систем до розв’язування текстових задач.
9. Лекція №3. Системи лінійних рівнянь
10. ЛІНЕАРИЗАЦІЯ НЕЛІНІЙНИХ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ
11. Логіка розв’язування рівнянь
12. Матрична форма запису системи лінійних рівнянь

Переглядів: 740