• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Евольвента кола і її властивості.

Еволютою називається геометричне місце центрів кривизни даної кривої. Дана крива по відношенню до еволюти називається евольвентою. Згідно визначенню нормаль до евольвенти ( на якій лежить центр кривизни ) є дотичною до еволюти. Евольвенти кола описуються точками прямої, що проводить, при її перекочуванні по колу, яке називають основним.

Властивості евольвенти кола:

Форма евольвенти кола визначається тільки радіусом основного кола rb. При евольвента переходить в пряму лінію.

Пряма, що проводить, є нормаллю до евольвенти в даній довільній точці My. Відрізок нормалі в довільній точці евольвенти lMyN = r дорівнює радіусу її кривизни і є дотичною до основного кола.

Евольвента має дві гілки і точку повернення М0, лежачу на основному колі. Евольвента не має крапок усередині основного кола.

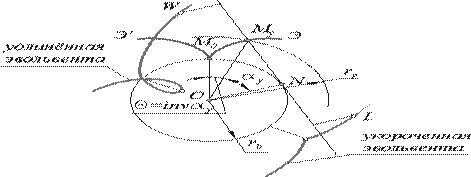
Крапки пов'язані з прямою, що проводить, але не лежачі на ній при перекочуванні описують: крапки розташовані прямою W, що вище проводить, - укорочені евольвенти, крапки, розташовані прямою L, що нижче проводить, - подовжені евольвенти.

Рис. 11.11

Параметричні рівняння евольвенти отримаємо з схеми, зображеної на Рис. 11.11 . Оскільки пряма, що проводить, перекочується по основному колу без ковзання те дуга М0n дорівнює відрізку NMy . Для дуги кола

з трикутника D OMyN

Звідки

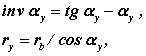
отримаємо|одержуватимемо| параметричні рівняння евольвенти.

Читайте також:

1. А) Товар і його властивості.
2. Алкани, їх хімічні властивості.
3. Аналізатори людини та їхні властивості.
4. Аналізатори людини та їхні властивості.
5. Будова атомів та хімічний зв’язок між атомами визначають будову сполук, а отже і їх фізичні та хімічні властивості.
6. Вектори. Лінійні дії над векторами. Властивості. Довжина вектора. Кут між векторами. Відстань між 2-ма точками. Проекція вектора на вісь. Координати вектора.
7. Векторний добуток і його властивості.
8. Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.
9. Властивості.
10. Диференціал функції. Застосування диференціала в наближених обчисленнях. Геометричний зміст диференціала і його властивості. Інваріантність.
11. Електронно-дірковий перехід і його властивості. Напівпровідникові діоди

Переглядів: 6408