Передмова

Zміністерство освіти і науки україни

Одеський національний політехнічний університет

Інститут заочної освіти

кафедра „природничо-наукової підготовки”

Методичні вказівки

Щодо виконання контролних робіт з предмету

„Теорія ймовірностей та математична статистика ”

для студентів усіх спеціальностей

Затверджено на засіданні кафедри

«Природничо-наукової підготовки»

Протокол № від “ ” __________ 200 р.

Одеса-2007

Методичні вказівки щодо виконання контролних робіт з предмету „Теорія ймовірностей та математична статистика ” / Уклад.: Г.Ф. Ускач – Одеса: ОНПУ, 2007. – 68 с.

Навчальне видання

Методичні вказівки

Щодо виконання контролних робіт з предмету

„Теорія ймовірностей та математична статистика ”

для студентів усіх спеціальностей

Укладач: Ускач Ганна Феліксівна,

асистент кафедри «Природничо-наукової

підготовки» Одеського національного

політехнічного університету

Рецензент Д.В. Буряк , к. фізико-мат. наук, викладач

Одеського національного

політехнічного університету

Зміст

Вступ 1. Випадкові величини та їх функції розподілу Види випадкових величин Дискретні випадкові величини Закон розподілу ймовірностей дискретної випадкової величини 1.2.2. Числові характеристики дискретних випадкових величин 1.2.3. Біномінальний розподіл 1.2.4. Розподіл Пуассона Неперервні випадкові величини Інтегральна функція розподілу неперервної випадкової величини 1.3.2. Диференційна функція розподілу неперервної випадкової величини 1.3.3. Числові характеристики неперервних випадкових величин 1.3.4. Рівномірний розподіл 1.3.5. Нормальний закон розподілу. 2. Елементи математичної статистики 2.1.Вибірковий метод 2.1.1. Генеральна і вибіркова сукупності 2.1.2. Статистичний розподіл вибірки 2.1.3. Емпірична функція розподілу 2.2.Статистичні оцінки параметрів розподілу 2.2.1. Точкові оцінки 2.2.2. Інтервальні оцінки 2.2.3. Надійний інтервал для оцінки математичного очікування нормального розподілу 2.2.4. Асиметрія і ексцес емпіричного розподілу 2.3.Перевірка гіпотези про нормальний розподіл генеральній сукупності по критерію Персона 2.4.Лінійна кореляція Контрольні завдання Список літератури Додаток 1 Додаток 2 Додаток 3 Додаток 4

Передмова

Мета даних методичних вказівок - допомогти студентам самостійно з мінімальними витратами часу виконати контрольні завдання з предмету «Теорія ймовірностей та математична статистика», які передбачені діючою програмою. Методичні вказівки охоплюють 2 основних розділи курсу «Теорії ймовірностей та математичної статистики»: елементи математичної статистики, випадкові величини та їх функції розподілу.

В методичних вказівках стисло викладені теоретичні відомості, які застосовуються при розв’язанні задач, а також приведені детальні розв’язки усіх типових задач.

В кінці методичних вказівок приведені таблиці значень функції:

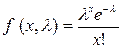
та таблиця критичних точок розподілу χ².

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Практична частина завдання	\|	Випадкові величини та їх функції розподілу

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.025 сек.