
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ЗАВДАННЯ ДО КОНТРОЛЬНОЇ РОБОТИ № 5-6
1. З колоди у 36 карт навмання обирають 4 карти. Знайти ймовірність того, що серед них три тузи.
2. Кидають два гральних кубика. Знайти ймовірність того, що сума очок, які випали дорівнює семи.
3. В урні 5 червоних та 6 білих кульок. Знайти ймовірність того, що навмання обрані дві кулі будуть різного кольору.
4. Монету кидають 4 рази. Знайти ймовірність того, що герб випадає рівно два рази.
5. Знайти ймовірність того, що, заповнивши картку лотереї «Спортлото» (5 з 36), учасник вгадає чотири номери.
6. У групі 30 студентів, з яких 10 здали сесію на відмінно. Групу поділили на дві рівні підгрупи. Знайти ймовірність того, що в кожній підгрупі опинилося 5 відмінників.
7. На семи картках написані букви: С, Т, У, Д, Е, Н, Т. Послідовно (навмання) беруть три з них. Знайти ймовірність того, що при цьому прочитається слово «СУД».
8. На тарілці 4 пиріжки з капустою та 6 з горохом. Знайти ймовірність того, що обранні навмання два з них виявляться з різною начинкою.
9. В парному телефонному номері забуті дві останні цифри. Знайти ймовірність того, що набраний навмання номер правильний.
10. На групу з 10 дівчат та 15 хлопців виділили 4 пільгові путівки, які вирішено було розіграти. Знайти ймовірність того, що серед щасливчиків виявляться 2 дівчини та 2 хлопця.
11. Знайти ймовірність того, що навмання взяте тризначне число буде: 1) кратним 3 або 5, 2) кратним 3 та 5 одночасно.
12. Три стрілка вражають мішень відповідно з ймовірностями 0,6; 0,7; 0,8. Знайти ймовірність того, що після залпу мішень вражена рівно двома пулями.
13. Гральний кубик кидають до появи шістки. Знайти ймовірність того, що потрібно буде кидати п’ятий раз.
14. Гравцю здають дві карти з колоди в 36 карт. Знайти ймовірність того, що дама та король однієї масті.
15. В коробці 6 червоних , 8 синіх та 11 зелених кульок. Навмання беруть по одному 3 кульки. Знайти ймовірність того, що послідовно з’являться зелена, синя та червона кульки, якщо вийнята кулька 1) не повертається знову в коробку; 2) знову повертається в коробку.
16. Студент знає 35 з 40 питань програми. Кожний екзаменаційний білет містить три питання. Знайти ймовірність того, що студент знає: 1) усі три питання; 2) тільки одне питання екзаменаційного білета.
17. Існує достатньо велика партія фасованого цукру по 0,5кг у кульку. Нормальною вважається маса від 0,495 до 0,505 кг. Ймовірність того, що маса кулька менша 0,495кг дорівнює 0,05; ймовірність того, що маса кулька більша 0,505кг дорівнює 0,10. З партії цукру навмання взяли два кульки. Знайти ймовірність того, що: 1) обидва кульки мають нормальну масу; 2) тільки один кульок має нормальну масу.
18. Булочки, які випускаються хлібозаводом мають такий розподіл за масою: менше 98г – 5%, більше 102г – 10%, інші 85% булочок мають нормальну масу (98г – 102г). З достатньо великої партії беруть навмання дві булочки. Знайти ймовірність того, що: 1) обидві булочки мають нормальну масу; 2) одна булочка має масу більше норми, а друга – менше норми.
19. Студент знає 30 білетів з 50. Чи зміниться ймовірність витягти вдалий білет, якщо студент зайде на іспит не першим, а другим.
20. Працівник обслуговує три станки. Ймовірність того, що протягом 1 години роботи уваги працівника потребуватиме перший станок, дорівнює 0,3; другий – 0,4; третій – 0,2. Знайти ймовірність того, що протягом 1 години роботи уваги працівника потребуватиме: 1) який-небудь один станок; 2) хоча б один станок.
21. До складу надходить продукція трьох фабрик. Продукція першої фабрики складає 25%, другої– 40%, третьої – 35%. Відомо також, що 4% виробів, які виготовлені на першій фабриці, є бракованими, друга фабрика випускає 1% бракованих виробів, а третя – 3% браку. Знайти ймовірність того, що вибраний навмання виріб зі складу виявиться стандартним.
22. До складу потрапляє продукція трьох фабрик. Продукція першої фабрики складає 25%, другої– 40%, третьої – 35%. Відомо, також, що 4% виробів, вироблених на першій фабриці, являються бракованими, друга фабрика випускає 1% бракованих виробів, а третя – 3% браку. Навмання взятий на складі виріб виявився нестандартним. Знайти ймовірність того, що він вироблений на першій фабриці.
23. Ймовірність того, що витрати електроенергії протягом доби не перевищить встановленої норми, дорівнює 0,75. Знайти ймовірність того, що у найближчі шість діб витрати електроенергії: 1) протягом чотирьох діб не перевищить норму; 2) протягом не менше ніж чотирьох діб не перевищить норму.
24. В першій коробці 10 кульок, з них 3 білих, а в другій коробці 15, з них білих – 4. З кожної коробки навмання взяли по одній кульці, з яких потім випадковим чином узяли одну кульку. Знайти ймовірність того, що була узята біла кулька.
25. В першій коробці 10 кульок, з них 3 білих, а в другій коробці 15, з них білих – 4. З першої коробки переклали у другу навмання узяту кульку, а потім з другої коробки узяли дві кульки. Знайти ймовірність того, що вони білі.
26. Ймовірність хоча б одного влучання при 4 незалежних пострілах дорівнює 0,9984. Знайти ймовірність влучання при одному пострілі.
27. На двох станках-автоматах виготовляються однакові деталі та скидаються на один и той самий транспортер. Продуктивність першого станка в три рази більша, ніж другого. Перший станок виробляє 7% нестандартних деталей, а другий – 2%. Навмання узята з транспортера деталь виявилась стандартною. Знайти ймовірність того, що вона вироблена першим станком.
28. Відомо, що 3% усієї продукції першого цеху та 5% продукції другого цеху – нестандартні вироби. На контроль поступив один навмання одібраний виріб з першого та один – з другого цеху. Яка ймовірність того, що хоча б один виріб – стандартний.
29. Ймовірність виходу з ладу виробу за час випробовування дорівнює 0,1. Яка ймовірність того, що за час випробовування 100 виробів вийде з ладу від 5 до 10 виробів?
30. Перший завод виробляє 40% виробів, а другий – 60%. Тільки 95% виробів першого заводу витримують гарантійний термін роботи без поломки, а другого – 98%. Навмання взятий виріб пропрацював гарантійний термін. Знайти ймовірність того, що його вироблено другим заводом.
31 – 40. Випадкова величина 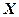 задана функцією розподілу
задана функцією розподілу 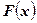 . Потрібно:
. Потрібно:
1) знайти щільність ймовірності 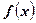 ;
;
2) обчислити математичне сподівання та дисперсію випадкової величини 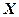 ;
;
3) побудувати графіки функції розподілу та щільності ймовірності.
31. 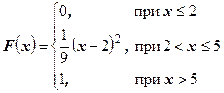
| 32. 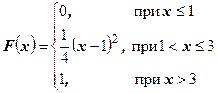
|
33. 
| 34. 
|
35. 
| 36. 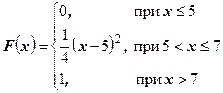
|
37. 
| 38. 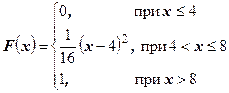
|
39. 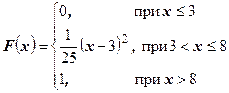
| 40. 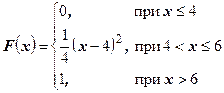
|
41 – 50. Знайти ймовірність попадання випадкової величини 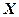 на відрізок
на відрізок  , якщо вона розподілена:
, якщо вона розподілена:
1) рівномірно на відрізку  ;
;
2) за нормальним законом та має математичне сподівання 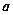 та середнє квадратичне відхилення
та середнє квадратичне відхилення  ;
;
41. 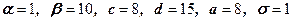
| 42. 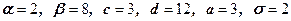
|
43. 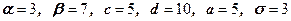
| 44. 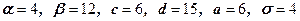
|
45. 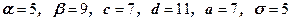
| 46. 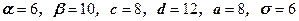
|
47. 
| 48. 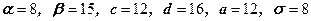
|
49. 
| 50. 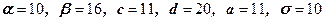
|
51 – 60. Задані значення 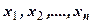 , які прийняла дискретна випадкова величина
, які прийняла дискретна випадкова величина 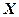 в послідовності
в послідовності 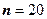 незалежних випробувань. Потрібно:
незалежних випробувань. Потрібно:
1) скласти емпіричний розподіл досліджуваної випадкової величини;
2) обчислити вибіркове (емпіричне) середнє 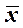 ;
;
3) обчислити виправлене середнє квадратичне відхилення 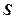 ;
;
4) побудувати графік емпіричної функції розподілу 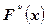 .
.
| 51) 3,5 3,8 4,0 4,2 4,3 4,4 3,8 4,0 4,3 4,0 3,5 4,4 4,2 4,0 3,5 4,2 4,4 4,0 4,3 4,3 | 52) 5,6 5,7 5,9 6,0 6,3 6,5 7,0 6,0 5,6 6,3 7,0 5,9 5,7 6,5 6,3 6,5 7,0 5,9 6,3 5,9 |
| 53) 7,8 8,0 8,1 8,3 8,6 8,7 8,9 8,3 8,7 8,0 7,8 8,9 8,3 8,7 8,1 8,6 8,3 7,8 8,1 8,0 | 54) 12,5 12,7 13,5 13,6 13,7 13,9 12,5 13,6 12,5 13,6 13,9 12,7 13,6 13,9 12,5 13,9 12,7 13,7 13,5 13,6 |
| 55) 8,4 8,9 9,3 8,3 9,7 9,8 8,8 8,8 9,3 8,4 9,3 8,4 9,7 9,3 8,3 8,4 9,7 8,8 8,9 9,3 | 56) 17,3 17,5 18,4 17,4 17,2 18,4 18,3 17,4 17,2 18,4 17,3 17,5 17,2 18,4 18,3 18,2 18,4 18,3 18,2 18,4 |
| 57) 12,3 20,0 19,9 18,1 14,4 13,6 18,1 13,6 12,3 19,9 20,0 14,4 18,1 13,6 19,9 13,6 14,4 13,6 19,9 20,0 | 58) 8,8 9,6 7,5 5,7 5,3 7,2 7,3 8,8 7,5 9,6 7,3 8,8 7,5 5,7 5,3 7,2 7,3 7,5 9,6 5,7 |
| 59) 2,8 3,4 5,5 6,6 3,3 3,5 6,4 2,8 6,4 3,4 3,4 3,5 5,6 6,5 6,6 3,3 3,5 5,5 5,6 3,3 | 60) 5,3 6,4 4,8 4,7 6,5 6,3 4,7 6,4 6,3 5,3 4,7 4,8 6,5 6,3 5,3 4,7 6,4 6,5 4,8 5,3 |
61 – 70. Знайти довірчий інтервал для оцінки математичного сподівання 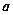 нормального розподілу з надійністю
нормального розподілу з надійністю 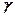 , знаючи вибіркове середнє
, знаючи вибіркове середнє 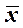 , об’єм вибірки
, об’єм вибірки 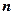 та середньоквадратичне відхилення
та середньоквадратичне відхилення  :
:
61. 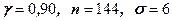 , , 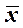 =10,2 =10,2
| 62. 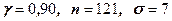 , , 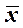 =15,1 =15,1
|
63.  , , 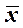 =14,6 =14,6
| 64.  , , 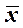 =10,5 =10,5
|
65.  , , 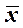 =13,2 =13,2
| 66. 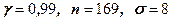 , , 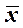 =14,7 =14,7
|
67. 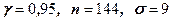 , , 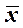 =18,0 =18,0
| 68. 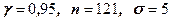 , , 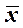 =25,1 =25,1
|
69. 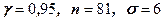 , , 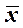 =43,2 =43,2
| 70. 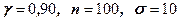 , , 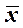 =19,1 =19,1
|
Читайте також:
- I. Аналіз контрольної роботи.
- I. Постановка завдання статистичного дослідження
- I. ПРЕДМЕТ, МЕТА ТА ЗАВДАННЯ ДИСЦИПЛІНИ
- II. Вимоги безпеки перед початком роботи
- II. Вимоги безпеки праці перед початком роботи
- II. Завдання на проект.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
| <== попередня сторінка | | | наступна сторінка ==> |
| ЗАВДАННЯ ДО КОНТРОЛЬНОЇ РОБОТИ № 3-4 | | | ЗАВДАННЯ ДО КОНТРОЛЬНОЇ РОБОТИ № 7-8 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |