• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Класичне, статистичне і геометричне означення ймовірності

Реально існує три означення ймовірності: класичне, статистичне і геометричне.

Якщо результати випробування можна подати у вигляді повної групи рівноможливих попарно несумісних випадкових подій, і якщо деяка подія 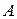з’являється тільки в 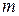випадках, то ймовірність події 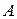дорівнює відношенню 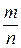. Звідки класичне означення ймовірності.

Означення 8. Ймовірність деякої події 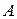є число, що дорівнює відношенню числа сприятливих випадків 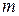появи події 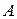до загального числа випадків

(1)

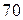Приклад. В коробці авторучок, з них з синьою пастою і – з червоною. Яка ймовірність того, що взята навмання ручка буде з синьою пастою?

Розв’язання. Подія 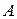– взята навмання ручка має синю пасту. Число загальних випадків випробування 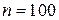, число випадків, що сприяють події 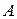– . За формулою

.

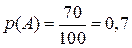Відносна частота події 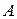визначається рівністю

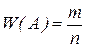, (2)

де 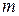– число випробувань, в яких подія 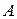відбулася; – загальне число проведених випробувань.

При статистичнім означенні за імовірність по дії приймають її відносну частоту.

Приклад. По цілі зробили пострілів, при цьому було зареєстровано 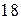влучень. Відносна частота влучення в ціль дорівнює

.

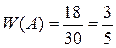Нехай відрізок складає частину відрізку . На відрізок навмання поставлена точка. Якщо припустить, що ймовірність попадання точки на відрізок пропорційна довжині цього відрізку і не залежить від його розташування відносно відрізку , то ймовірність попадання точки на відрізок визначається рівністю

(3)

Аналогічно визначається ймовірність попадання точки в плоску і просторову фігури:

або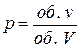

Приклад. На площині намальовані два концентричних кола, радіуси яких і 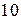см відповідно. Знайти ймовірність того, що точка, кинута навмання в більше коло, попаде в кільце, утворене побудованими колами. Передбачається, що ймовірність попадання точки в плоску фігуру пропорційна площі цієї фігури і не залежить від її розташування відносно більшого кола.

Розв’язання.

Площа меншого кільця (фігура ) .

Площа більшого кола (фігура ) .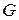

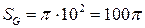Шукана ймовірність .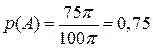

З означення ймовірності випливають теореми про її властивості.

Теорема 1. Ймовірність любої випадкової події є додатне число, що міститься між нулем і одиницею

.

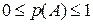Доведення.Число випадків 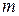, сприятливих любій події, не може бути від’ємним і більшим ніж їх загальне число , тобто . Ділення нерівності почленно на дає , або прийнявши до уваги рівність (1), отримаємо:

, що і треба було довести.

Теорема 2. Імовірність достовірної події дорівнює

.

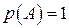Доведення.Властивість очевидна, оскільки достовірній події повинні сприяти усі єдино можливих, рівноможливих і несумісних випадків, тобто .

Теорема 3. Ймовірність неможливої події дорівнює нулю.

Читайте також:

1. Банкрутство підприємства: причини, оцінка ймовірності настання та наслідки
2. Визначення ймовірності перерви електропостачання і середньої кількості недоотриманої електроенергії.
3. Геометричне тлумачення мішаного добутку векторів.
4. Геометричні ймовірності
5. Границя функції. Означення границі функції за Гейне й за Коші.
6. Графічне позначення матеріалу в перерізах і на виді - штрихування, що виконується тонкими суцільними лініями.
7. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.
8. Джерела відомостей про шлюби і шлюбний стан та їх статистичне вивчення.
9. Допустимий критичний та катастрофічний ризик. Крива щільності розподілу ймовірності настання випадкових втрат.
10. Екологія: означення, мета і завдання екології як науки
11. Загальні вимоги до оформлення геологічних карт. Умовні позначення на геологічній графіці.
12. Ймовірність відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях

Переглядів: 3088