• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Парна лінійна регресія

Парний регресійний аналіз спрямований на визначення ступеню зв’язку між змінними і яким чином вони пов’язані в побудові парної моделі. Слід відзначити, що не слід очікувати отримання точного співвідношення між будь-якими економічними показниками, крім випадків, коли воно існує по визначенню.

Парний регресійний аналіз відбувається за наступними напрямами:

1. Збір статистичної інформації, яка відображає економічні процесі на підприємстві. Цей процес відбувається шляхом обробки фінансових, економічних, бухгалтерських, статистичних документів діяльності суб’єктів підприємницької діяльності.

2. Обробка статистичної інформації, її специфікація. Це важливий етап, оскільки він створює підґрунтя для отримання об’єктивних результатів і адекватної парної економетричної моделі.

3. Використання економетричного інструментарію для розробки парної моделі. В цьому аспектів здійснюється побудова матриці статистики, оцінка показників варіації змінних, розрахунок коефіцієнтів парної кореляції й детермінації (див. розділ 9.2), визначення показників параметрів парної економетричної моделі. Слід відзначити, що для обчислення параметрів рівняння виду 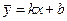(лінійна парна модель залежності) частіш за все користуються методом найменших квадратів. При цьому ставиться умова, щоб сума квадратів відхилень (відстаней) всіх досліджених точок від ординат, обчислених за рівнянням прямої ε_i, була мінімальною. Іншими словами, пряма повинна проходити якомога ближче до вершин емпіричної лінії регресії. Це означає, що параметри К і b управління регресії треба визначити з рівняння:

, (9.19)

де y_i – ординати досліджуваних точок;

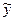_i – ординати розрахункових точок, визначені за рівнянням регресії =к х_i+ b таким чином .

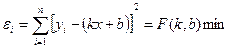Умовою екстремуму даної функції слід вважати рівність нулю часткових виробничих, узятих за параметрами К і b

звідси (9.20)

Скоротивши на (-2) і розкривши квадратні дужки, отримаємо систему лінійних рівнянь

(9.21)

підставивши сюди чисельні значення відповідних величин, знайдемо параметри К і b.

У разі лінійної залежності геометричне і алгебраїчне значення коефіцієнта регресії полягає в тому, що він кількісно характеризує на скільки в середньому змінюється у при зміні Хi на одиницю свого вимірювання. Чим більше чисельні значення коефіцієнта регресії, тим більше відносний приріст функції при зміні аргументу.

4. Оцінка адекватності розробленої парної лінійної економетричної моделі на основі критеріїв і тестів, представлених в розділах 9.2 і 9.3.

5. Інтерпретація отриманих параметрів парної лінійної економетричної моделі. Це важливий етап, на якому відображається економічна результативність економетричного моделювання.

В загальному вигляді економетрична модель парної лінійної регресії може мати вигляд:

у = а₀ + а₁х +е, (9.22)

де у – залежна змінна;

х – незалежна змінна;

а₀, а₁ – параметри економетричного рівняння;

е – випадковий член.

Таким чином, парний регресійний аналіз дозволяє побудувати парну лінійну економетричну модель, яка дозволить встановити причинно-наслідковий зв’язок між залежною економічною змінною і незалежним фактором і створити передумови для побудови організаційно-економічних механізмів управління підприємствами та прийняття рішень, спрямованих на розвиток цих суб’єктів підприємницької діяльності. Проте більшість економічних процесів мають складний характер, де враховуються велика кількість факторів. Тому необхідно будувати економетричні моделі, які враховують декілька економічних показників, тобто розробляти лінійні моделі множинної регресії.

Читайте також:

1. Багатомірна лінійна модель регресії.
2. Загальна лінійна оптимізаційна модель Канторовича
3. Засобами композиції є лінії, штриховка (штрих), тонові й кольорові плями, світлотінь, лінійна і повітряна перспективи [5].
4. Лінійна витрата палива
5. Лінійна і квадратична локальні інтерполяції
6. Лінійна і об’ємна швидкості руху крові у різних ділянках судинного русла. Фактори, що впливають на їх величину.
7. Лінійна множинна регресія.
8. Лінійна модель міжнародної торгівлі
9. Лінійна модель торгівлі.
10. Лінійна модель трансферу технологій
11. Лінійна організаційна структура
12. Лінійна регресія за допомогою функцій, лінійного тренду та пакета аналізу

Переглядів: 3327