
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Перевірка відповідності реального потоку моделі найпростішого
Для такої перевірки використовують 2 підходи, залежно від того, які вимірювання здійснювались для реального потоку.
І спосіб.
Якщо підраховувалась кількість викликів, що потрапили до послідовності часових інтервалів заданої довжини, то перевіряється їх відповідність розподілу Пуассона, тобто рівність математичного очікування та дисперсії.
Таким чином, якщо задана таблиця статистичного розподілу випадкової величини у вигляді (табл.2.1), то при Mx ≈ Dx потік можна вважати найпростішим.
Таблиця 2.1
Статистичний розподіл кількості викликів потоку, що потрапили у заданий інтервал
| x(t)і | x(t)1 | x(t)2 | … | x(t)k |
| nі | n1 | n2 | … | nk |
де x(t)і – кількість викликів, що попали у nі інтервалів, якщо загальна кількість інтервалів  .
.
Статистичні оцінки математичного очікування та дисперсії числа викликів, що потрапили до кожного інтервалу:
 , (2.2)
, (2.2)
 . (2.3)
. (2.3)
ІІ спосіб.
Якщо вимірювались інтервали часу між двома послідовними викликами, то перевіряється їх відповідність експоненціальному розподілу, тобто рівність математичного очікування та середньо-квадратичне відхилення. Таким чином, якщо задана таблиця статистичного розподілу випадкової величини у вигляді (табл. 2.2), то при Mz ≈ σz потік можна вважати найпростішим.
Таблиця 2.2
Статистичний розподіл інтервалу між послідовними викликами потоку
| zі | z1 | z2 | … | zk |
| nі | n1 | n2 | … | nk |
де zі – значення часу між послідовними викликами;nі – кількість таких значень, якщо загальна кількість вимірів 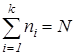 .
.
Статистичні оцінки математичного очікування, дисперсії та СКВ значеннь часу між послідовними викликами:
 , (2.2)
, (2.2)
 , (2.3)
, (2.3)
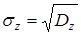 . (2.4)
. (2.4)
2. Порядок виконання роботи:
2.1. Промоделювати два найпростіших потоки. Використати методику 2.1-2.6 л.р. №1. Прийняти параметри відповідно  ;
; 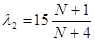 . Таблицю статистичного розподілу навести у вигляді:
. Таблицю статистичного розподілу навести у вигляді:
| Nинт | . . . | ||
| x1(t ) | |||
| x2(t ) | |||
| x1+x2 |
2.2. Побудувати графіки х1(n), x2(n), x(n), де n – № інтервалу, х1, x2, x – кількість викликів, потрапивши в інтервал для I, II і сумарного потоку.
2.3. Для сумарного потоку отримати lсум модельне (аналогічно п. 2.8 л. р. №1).
2.4. Порівняти отримане значення lсум і 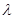 1+
1+ 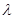 2 .
2 .
2.5. Здійснити перевірку відповідності змодельованого сумарного потоку моделі найпростішого.
Зробити висновки.
3. Контрольні питання.
3.1. Який потік утворюється при об’єднанні n найпростіших потоків ?
3.2. Чому дорівнюють параметри потоків, утворених при роз’єднанні найпростішого потоку?
3.3. Який спосіб перевірки відповідності реального потоку моделі найпростішого використовують, якщо :
а) виміряні проміжки між викликами потоку?
б) підраховано число викликів, що потрапили до інтервалів рівної довжини?
3.4. В чому полягає сутність методу Монте-Карло?
3.5. Які максимуми має розподіл Пуассона?
3.6. Скільки джерел викликів в найпростішому потоці і якою його властивістю це пояснюється?
ЛАБОРАТОРНА РоБОТА № 3
дослідження навантаження в телефонних мережах
Мета: Дослідити процес формування та обслуговування навантаження в телефонних мережах. Обчислити вхідне, обслуговане та втрачене навантаження та порівняти з теоретичними значеннями
Читайте також:
- CMM. Визначення моделі зрілості.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- III. GPSS — програма імітаційної моделі ЕОМ
- ISO 15504.Структура еталонної моделі
| <== попередня сторінка | | | наступна сторінка ==> |
| Теоретичні відомості | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |