
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
РОЗДІЛ 3. ЛОГІКА ВИСЛОВЛЕНЬ ТА ПРЕДИКАТІВ
Висловлення − це твердження, яке може бути істинним або хибним.
У математичній логіці вважають кожне висловлення або істинним, або хибним і не припускають можливості існування такого висловлення, яке б водночас було і істинним, і хибним. Якщо висловлення мають однакові значення істинності, то це можна записати за допомогою знаку =, тобто A =B.
Якщо висловлення складається принаймні з двох простих висловлень, то воно називається складним. Наприклад висловлення A = “17 − просте число, 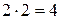 ” − складне висловлення, яке складається з двох простих: “17 − просте число” і “
” − складне висловлення, яке складається з двох простих: “17 − просте число” і “ 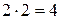 ”.
”.
Складні висловлення утворюються з простих за допомогою так званих логічних операцій. До основних логічних операцій відносяться заперечення,кон’юнкція, диз’юнкція, імплікація та еквіваленція. Для цих операцій використовуються ті ж позначення, що і в алгебрі логіки. При цьому таблиці відповідності тут називаються таблицями істинності.
Запереченням висловлення А називається таке складне висловлення 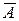 (читається “не А”), яке хибне, якщо А істинне, і істинне, якщо А хибне.
(читається “не А”), яке хибне, якщо А істинне, і істинне, якщо А хибне.
Кон’юнкцією двох висловлень А і В називається таке складне висловлення A Ù B (читається “ А і В”), яке істинне тоді і тільки тоді, коли істинні обидва висловлення А і В,що його утворюють, і хибне у всіх інших випадках.
Диз’юнкцією двох висловлень А і В називається таке складне висловлення A Ú B (читається “ А або В”), яке хибне тоді і тільки тоді, коли хибні обидва висловлення А і В,що його утворюють, і істинне у всіх інших випадках.
Імплікацієюдвох висловлень А і Вназивається таке складне висловлення A ® B (читається “якщо А, то В”), яке хибне тоді і тільки тоді, коли А істинне, а В − хибне.
Еквіваленцієюдвох висловлень А і Вназивається таке складне висловлення А~ В (читається “ А, якщо і тільки якщо В”), яке істинне тоді і тільки тоді, коли значення істинності висловлень А і В однакові, і хибне − якщо різні.
Будь-яке складне висловлення, яке складається із простих висловлень, зв’язаних сентенціональними зв’язками (”не”, “і”, “або”, “якщо…, то…”, “якщо і тільки якщо”), можна подати в символічній формі. В результаті одержимо висловлювальну формулу. На кожному наборі значень істинності букв (змінних) формула набуває деякого значення. Отже, будь-яку формулу логіки висловлень можна розглядати як функцію істинності.
Тотожно істинна формула, тобто така формула, яка набуває значення 1 при будь-яких значеннях її аргументів, називається тавтологією. Тотожно хибна формула на всіх наборах її аргументів набуває значення 0 і називається протиріччям.
Можна також використати залежності 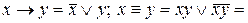
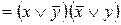 і перетворити висловлювальну формулу до нормальної форми. Якщо хоч би один член диз’юнктивної нормальної форми буде рівним 1, то відповідна їй формула є тавтологією. Якщо хоч би один член кон’юнктивної нормальної форми буде рівним 0, то відповідна їй формула буде протиріччям. Для того, щоб вказати, що дана формула є тавтологією, використовується символ ê=, який записують перед формулою.
і перетворити висловлювальну формулу до нормальної форми. Якщо хоч би один член диз’юнктивної нормальної форми буде рівним 1, то відповідна їй формула є тавтологією. Якщо хоч би один член кон’юнктивної нормальної форми буде рівним 0, то відповідна їй формула буде протиріччям. Для того, щоб вказати, що дана формула є тавтологією, використовується символ ê=, який записують перед формулою.
Дві формули називаються рівносильними, якщо на всіх наборах значень змінних, що в них входять, ці формули набувають однакового значення. Для позначення цього відношення використовують символ Û.
Між відношенням рівносильності і еквіваленцією формул існує наступний зв’язок: якщо А і В − рівносильні, то A~B− тавтологія, і навпаки, якщо A~B − тавтологія, то А і В − рівносильні. Отже, тавтології можна одержувати із рівносильностей заміною знаку Û на ~. Так, із рівносильності A Ú AB Û A одержимо тавтологію ê=(A Ú AB) ~ A.
Кажуть, що формула В є логічним висновком формули А і пишуть
AÞ B, якщо В істинне на всіх наборах значень змінних, для яких А істинне. Легко переконатися, що AÞ B тоді і тільки тоді, коли ê=A® B. Отже, якщо A® B − тавтологія, то із істинності 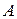 завжди випливає істинність
завжди випливає істинність 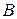 , тобто AÞ B. Навпаки, якщо AÞ B, то виключається випадок, коли
, тобто AÞ B. Навпаки, якщо AÞ B, то виключається випадок, коли 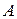 істинне, а
істинне, а 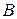 хибне, отже, A® B істинне на всіх наборах значень змінних, тобто ê=A® B.
хибне, отже, A® B істинне на всіх наборах значень змінних, тобто ê=A® B.
Висловлення виражають властивості одного чи кількох об’єктів. Змістовна частина висловлення відіграє роль визначальної властивості сукупності об’єктів, для яких це висловлення істинне, і називається предикатом. Наприклад, висловлення “1– корінь квадратного рівняння x2 + 3x – 4 =0 ” може бути істинним або хибним в залежності від того, які насправді корені даного рівняння. В той же час предикат “x– корінь квадратного рівняння x2 + 3x – 4 =0 ” визначає підмножину чисел на множині дійсних чисел. Підставивши замість 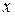 певне число, одержимо множину висловлень. Сукупність істинних висловлень і буде визначати множину коренів даного рівняння.
певне число, одержимо множину висловлень. Сукупність істинних висловлень і буде визначати множину коренів даного рівняння.
В логіці предикатів велике значення мають дві операції, які називаються кванторами, за допомогою яких виражають відношення спільності і існування. Нехай P(x) − предикат, визначений на множині M. Твердження, що всі x Î M мають властивість P(x), записують за допомогою квантора загальності "x у вигляді "xP(x), що читається “для всіх x P від x”. Твердження, що існує хоч би один об’єкт x із M, який має властивість P(x), записують за допомогою квантора існування $x у вигляді $xP(x), що читається “існує таке x, що P від x”.
Хоч у виразах "xP(x) і $xP(x) і зустрічається буква x, але вони не залежать від значення цієї змінної. Квантори "x і $x зв’язують змінну x, перетворюючи одномісний предикат у висловлення. Очевидно, "xP(x) істинне тільки за умови, що P(x) тотожно істинний предикат, а у всіх інших випадках це висловлення хибне. Висловлення $xP(x) завжди істинне, крім єдиного випадку, коли P(x) − тотожно хибний предикат.
Розглянемо, наприклад, предикат P(x) = “ 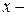 просте число”, визначений на множині натуральних чисел. Висловлення "xP(x) − “всі натуральні числа прості” − хибне, а $xP(x) − “деякі з натуральних чисел − прості” − істинне.
просте число”, визначений на множині натуральних чисел. Висловлення "xP(x) − “всі натуральні числа прості” − хибне, а $xP(x) − “деякі з натуральних чисел − прості” − істинне.
Питання для самоперевірки
1.Що таке висловлення? Наведіть приклади.
2.Назвіть основні логічні операції, дайте їх означення.
3. Що таке сентенціональні зв’язки?
4.Які висловлення називаються складними?
5. Що таке тавтологія?
6.Назвіть основні закони логіки висловлень.
7. Що таке рівносильність? Який зв'язок між рівносильністю і екві-
валенцією?
8. Що таке логічний наслідок? Який зв'язок між логічним наслідком
і еквіваленцією?
9. Що таке предикат?
10. Який зміст понять кванторів спільності і існування?
Література: [2], c. 43-58.
Вправи
71.Доведіть закони логіки висловлень (тавтології).
72. Доведіть наступні рівносильності:
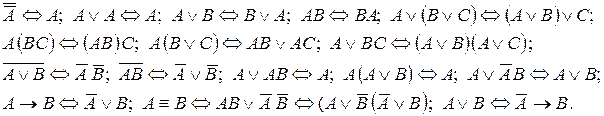 73. Доведіть через відповідну тавтологію логічний висновок
73. Доведіть через відповідну тавтологію логічний висновок
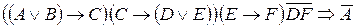 (
( 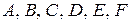 – деякі висловлення).
– деякі висловлення).
74. Дослідити кожну із наведених систем висловлень на суперечливість:
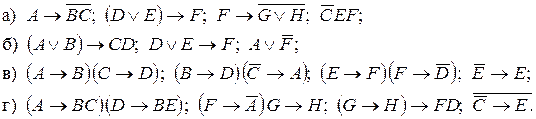
75. На множині натуральних чисел визначені предикати: 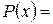 “число x ділиться на 8” і Q(x) = “x– парне число”. Прочитайте наступні висловлення та виясніть, які з них істинні: а)
“число x ділиться на 8” і Q(x) = “x– парне число”. Прочитайте наступні висловлення та виясніть, які з них істинні: а) 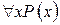 ; б)
; б) 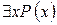 ; в)
; в) 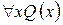 ; г)
; г) 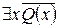 ;
;
д) 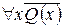 ; е)
; е) 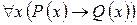 ; є)
; є) 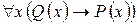 ; ж)
; ж) 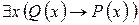 .
.
76.Граф G = (V, E) визначається заданням непорожньої множини вершин V множини ребер E і тримісного предиката P(x, e, y) = “ребро e з’єднує вершини x i y”, який визначений на всіх упорядкованих трійках (x, e, y), причому x, y Î V i e Î E (для орграфа x вважається початковою, аy– кінцевою вершинами дугиe). Напишіть предикати, які задають
а) підмножину дуг орграфа, які виходять з вершини a;
б) підмножину дуг орграфа, які входять у вершину b;
в) підмножину ребер графа, інцидентних вершині a;
г) підмножину ребер графа, які з’єднують вершини a і b.
77. У відповідності з визначенням графа із задачі 76 розшифруйте наступні висловлення:
а) 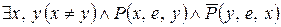 ;
;
б)  ;
;
в) 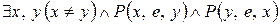 .
.
78. На множині натуральних чисел визначені предикати: P(x) = “ x – просте число”, Q(x) = “x– парне число”, R(x, y) = “x не дорівнює y”. Прочитайте наступне висловлення:
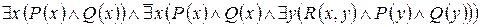 .
.
Читайте також:
- IV розділ. Сегментація ринку та вибір цільового сегменту
- IІI розділ. Аналіз стану маркетингового середовища підприємства
- V розділ. Товарна політика підприємства
- VI розділ. Маркетингова цінова політика
- VII розділ. Маркетингові рішення з розподілу та збуту товару
- VIII розділ. Маркетингова політика комунікацій
- А) Роздільне складання таблиць (За підручником Богдановича М.В.)
- Аварійно-рятувальні підрозділи Оперативно-рятувальної служби цивільного захисту, їх призначення і склад.
- Актив і пасив балансу складаються також з певних розділів.
- Активи, що реалізуються повільно (А3) – це статті 2-го розділу активу балансу, які включають запаси та інші оборотні активи (рядки 100 до 140 включно, а також рядок 250).
- Аналіз бойових дій пожежних підрозділів
- Аргументація і пралогіка
| <== попередня сторінка | | | наступна сторінка ==> |
| Контактні та логічні схеми | | | РОЗДІЛ 4. ГРАФИ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |