Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Приклади розв’язування типових задач з «Регіональної економіки»

На практичних заняттях з «Регіональної економіки» використовують низку типових задач з:

а) розрахунку виробничо-збутової зони підприємства;

б) вибору найоптимальнішого варіанту розміщення виробництва;

в) з оцінки ефективності діяльності підприємств;

г) оцінки рівня розвитку регіонів та ін.

А) Типові задачі з обрахування збутової зони підприємств можна вирішити за формулою: Р = (П₂– П₁+ Т₂Д): (Т₁+ Т₂), де П₁, П₂ – приведені витрати на виробництво продукції підприємствами 1 і 2, Д – відстань між підприємствами, Т₁, і Т₂ – витрати на перевезення одиниці продукції на відстань 1 км від 1-го підприємства до другого і від 2-го до першого. Часто студентам важко запам’ятати цю формулу. Це зовсім не обов’язково. Треба зрозуміти економічну суть задачі і з допомогою найпростіших арифметичних дій вирішити її.

Приклад вирішення задачі: П₁ на першому підприємстві – 20 грн. П₂ на другому підприємстві – 30 грн., Т₁= 2 грн., Т₂ = 1 грн. Д = 1000 км. Перше підприємство збуває свою продукцію на відстані х км, друге підприємство – відповідно на відстані (1000 – х) км. На відстані х від першого підприємства і на відстані (1000 – х) від другого підприємства витрати на виробництво і перевезення продукції від 1-го підприємства у бік 2-го дорівнюють витратам на виробництво і перевезення продукції від 2-го підприємства у бік 1-го. Складаємо просте порівняння з одним невідомим:

П₁ + Т₁ Х = П₂ + Т₂ (Д – Х),

20 грн. + 2 грн./км Х = 30 грн. + 1 грн./км (1000 км – Х),

2х = 3 0 – 20 + 1000 – Х,

3х = 1010,

х = 303 км,

Д – Х = 1000 – 303 = 697 км.

Таким чином, від 1-го підприємства вигідно вивозити продукцію на відстань 303 км., а від 2-го – на відстань 697 км.

Б). Задачі з вибору найефективнішого варіанту розміщення підприємства вирішують з допомогою формули приведених витрат (затрат): П = С + Е К → min, де П – приведені витрати; С – собівартість виробництва (поточні або тимчасові витрати), тобто це всі витрати на виробництво одиниці продукції, які включають у себе витрати на матеріали, сировину, паливо, енергію, заробітну плату, амортизаційні та інші витрати; К – капітальні вкладення (одноразові витрати, або кошторисна вартість), тобто це витрати на будівництво підприємства, його обладнання; Е – коефіцієнт ефективності капітальних вкладень, якій дорівнює Е = , де t – строк окупності капітальних вкладень. Таким чином, С розраховано на конкретний рік, а К надається на весь строк експлуатації підприємства. Коефіцієнт ефективності капітальних вкладень служить для “приведення“ капітальних вкладень на один рік (за такій рік приймають один рік окупності капітальних витрат). Тому ця формула і називається “формулою приведених витрат“. За кожним варіантом розміщення розраховують приведені витрати. Найефективнішим буде варіант, в якому витрати найменші. Відповідно, дохід, який визначається, як різниця між ціною продажу продукції і витратами на її виробництво, буде максимальним.

Приклад вирішення задачі. Є три варіанти розміщення підприємства. У першому варіанті собівартість продукції дорівнює 180 грн., капітальні витрати – 240 грн.; відповідно, у другому варіанті: С = 150 грн., К = 2000 грн.; у третьому варіанті: С = 200 грн., К = 1800 грн.; робимо розрахунки (коефіцієнт Е приймається нормативним – 0,12; для сільського господарства він дорівнює 0,1):

П₁= 180 грн. + 0,12 х2400 грн. = 468 грн.,

П₂ = 150 грн. + 0,12 х2000 грн. = 390 грн.,

П₃ = 200 грн. + 0,12 х1800 грн. = 416 грн.

Вибираємо другий варіант, тому що витрати тут найменші, відповідно, дохід, який можна отримати, буде максимальним.

В). Оцінка ефективності підприємства може здійснюватися за різними формулами:

а) розрахунок повного економічного ефекту (доходу) за рік:

Е = Д = Ц – С , де Д – річний дохід; Ц – ціна, за якою продана продукція; С – собівартість виробництва, яка включає у себе також усі податкові виплати, що передбачені законом.

Приклад вирішення задачі. Пшеницею засіяно 200 га орних земель. Урожайність при внесенні одиниці добрив на 1 га, дає добавку до врожаю 0,1 ц /га. Заготівельна ціна на зерно – 120 грн./ц. Собівартість зерна для господарства – 90 грн./ц. На поле внесено 120 од. добрив на 1 га. Визначити економічний ефект від зернового господарства при внесенні добрив.

Підрахуємо на скільки збільшився урожай при внесенні добрив на усьому полі: 120х0,1 ц/га х200 га = 2400 ц. Дохід від продажу 1 ц пшениці становить (заготівельна ціна мінус собівартість виробництва): 120 грн./ц – 90 грн./ц = 30 грн./ц. Відповідно, дохід від додаткової кількості пшениці, яка отримана за рахунок внесення добрив, становить: 30 грн./ц х2400 = 72000 грн.;

б) розрахунок абсолютної економічної ефективності визначається, як відношення отриманого річного доходу до витрат на його виробництво:

Е_абс. = 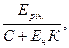де

Е_річ. – річний дохід (можна позначити також знаком “Д”, як у попередній задачі); С + Е_н К – приведені витрати; Е_абс. – абсолютна економічна ефективність. Це – безрозмірна величина (на відміну від “Д”). За своєю суттю це є коефіцієнт. Він показує, скільки одиниць доходу дає одиниця витрат. Чим він більший, тим, відповідно, підприємство працює ефективніше.

Приклад вирішення задачі. Два підприємства отримали річний дохід 6 млн.грн. і 8 млн.грн. Приведені витрати склали, відповідно, 8 млн. грн. і 10 млн.грн. Яке з цих підприємств працює ефективніше ?

Спочатку розрахуємо коефіцієнт абсолютної економічної ефективності для кожного підприємства за формулою:

Е = 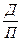, або Е = ,

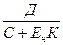Е₁ = 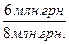= 0,75 , Е₂ = 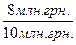= 0,8 .

Коефіцієнт Е₂ більший від Е₁, відповідно, друге підприємство, при інших рівних умовах, працює ліпше, ніж перше;

в) ефективність виробництва визначається також показниками: фондовіддачі; продуктивності праці; рентабельності; енерго- і ресурсомісткості та іншими.

Г). Рівень розвитку регіонів можна визначити за допомогою методу індексів. Його суть полягає в тому, що середній показник по країні приймають за 1 або за 100 %. Аналогічні показники по регіонах країни розраховують відносно середнього по країні, потім проводять ранжування регіонів за розрахованим індексом. Райони з індексом більшим, ніж “1“, відповідно, мають високий рівень розвитку (за показником, який розглядається).

Показники спеціалізації можна визначити за такими формулами:

1) К_мс = 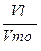100%, де

К_мс – коефіцієнт міжрайонної спеціалізації; V_l – обсяг продукції, що вивозиться за межі району; V_мо – обсяг цієї ж продукції у міжрайонному обміні країни.

Приклад вирішення задачі. Обсяг видобутку нафти в районі становить 2,5 млн. т; за межі регіону вивозиться 2 млн. т; загальний обсяг нафти, яка перевозиться у межах країни (внутрішні перевезення), – 5 млн. т. Визначити, чи належить видобуток нафти у цьому регіоні до галузей спеціалізації, чи ні.

Розрахуємо коефіцієнт міжрайонної спеціалізації:

К_м.с. = = 0,4.

К_м.с. – максимальний може дорівнювати 1; звичайно, він менший від одиниці. У нашому варіанті К_м.с. = 0,4. Це становить 40 % міжрайонного обміну даної продукції. Це – значна величина. Відповідно, нафтовидобувна промисловість цього району належить до галузей спеціалізації.

2) К_т = , де

К_т – коефіцієнт товарності продукції; V_в – обсяг продукції, що вивозиться за межі району у вартісному виразі; V_р – обсяг усієї подібної продукції, яку виробляє район у вартісному виразі. По суті, це – питома вага продукції , яку вивозять за межі району, від загального обсягу виробництва цієї продукції в районі.

Приклад вирішення задачі. Нафтопереробна промисловість району продає продукції за межі регіону на суму 15 млн. грн. Всього ця галузь випускає продукції на 25 млн. грн.

Розрахуємо коефіцієнт товарності:

К_т = = 0,6.

К_т = 0,6, тобто 60 % продукції нафтопереробної галузі вивозиться за межі району. Цю галузь можна віднести до галузей спеціалізації. К_т – може дорівнювати 1, або бути меншим. Чим ближчий коефіцієнт товарності до одиниці, тим більший ступінь спеціалізації галузі.

3) К_л = , де

К_л – коефіцієнт локалізації галузі в районі; К_в – частка галузі в загальному виробництві всієї продукції в районі; К_г – частка даної галузі по країні у загальному виробництві продукції всієї країни.

Приклад вирішення задачі. Машинобудування дає 20 % всієї продукції району, харчова промисловість – 50%. Машинобудування країни має питому вагу у загальному виробництві в країні 40 % , харчова – 20 % .

Визначити, які галузі належать до галузей спеціалізації.

Розрахуємо коефіцієнти локалізації для кожної галузі:

К_л = = = 0,5; К_л = = = 2,5.

Харчова промисловість є галуззю спеціалізації, тому що К_л для цієї галузі в районі більший за одиницю. Виробництво належить до галузей спеціалізації, коли його коефіцієнт локалізації дорівнює або більший за одиницю.

4) К_в = 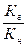, де

К_в – коефіцієнт виробництва продукції в районі на душу населення; К_г – частка продукції галузі району у виробництві подібної продукції в країні; К_н – частка населення району в загальній чисельності населення країни.

Приклад вирішення задачі. В районі проживає 5 % населення країни. Машинобудування району дає 10 % продукції машинобудування країни; хімічна промисловість району дає 3 % продукції хімічної промисловості країни. Визначити, яка з цих галузей належить до галузей спеціалізації.

Розрахуємо коефіцієнти для кожної галузі:

для машинобудування К_в= = = 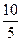2; для хімічної промисловості К_в = = = 0,6.

До галузей спеціалізації району належить машинобудування, тому що К_в має бути більшим або дорівнювати одиниці.

5) можна визначити також загальний індекс районної спеціалізації (С):

С = С_л С_с, де

С_л – індекс (коефіцієнт) локалізації; С_с – індекс ефективності виробництва (відношення обсягу виробництва на одиницю витрат у районі до аналогічного показника по країні). Останній показник показує, у скільки разів одержаний в районі ефект більший або менший від середнього по країні. Галузь належить до спеціалізованих, якщо індекс спеціалізації дорівнює або більший за одиницю.

Приклад вирішення задачі. В районі машинобудування має С_л = 1,5, хімічна промисловість – С_л = 0,9. Обсяг виробництва на одиницю витрат в районному машинобудуванні становить 10 (в країні 5), в хімічній промисловості – 20 (в країні 15). Визначити, яка з цих галузей належить до галузей спеціалізації.

Спочатку визначимо С_с для кожної галузі:

для машинобудування С_с = 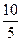= 2; для хімічної промисловості С_с = 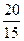= 1,3.

Далі визначаємо С:

для машинобудування С = 1,5х2 = 3;

для хімічної промисловості С = 0,9х1,3 = 1,2.

Висновок: обидві галузі належать до галузей спеціалізації, тому що мають С більший за 1.

6) часто потрібно визначити рівень комплексного розвитку господарства району (К_к). Цього досягають за формулою:

К_к = (У_1р У_2р) : (У_1п У_2п), де

У_1р,У_2р – питома вага району в країні за основними економічними ресурсами, наприклад, трудовими, паливними; У_1п,У_2п – частка відповідних галузей, наприклад, трудо- і паливомістких.

Приклад вирішення задачі.Є два райони. В першому частка паливних ресурсів становить 20 % від загальнодержавних, у другому – 30 % . В першому районі частка галузей, які використовують паливо, становить 10 %; в другому – 20 %. Визначити, у якому районі рівень комплексного використання паливних ресурсів вищий.

Розрахуємо коефіцієнт комплексного розвитку для кожного району:

К₁ = 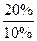= 2; К₂ = 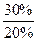= 1,5.

Рівень комплексного використання вищий у другому районі, тому що К найменший.

К не може бути меншим за одиницю, тому що не може бути використано ресурсів більше, ніж їх є (в іншому випадку це означає, що частка ресурсу ввозиться в район). У випадку, коли К набагато більший за 1, це означає, що значна частка ресурсу не використовується. Тобто в ідеалі К наближається до 1. Отже, ресурс використовується найповніше.

В даній задачі було розраховано коефіцієнт комплексності використання тільки одного ресурсу. Для визначення показника повної комплексності необхідно врахувати всі ресурси і всі галузі, які їх використовують.

Приклад вирішення задачі. Введене до ладу підприємство за рік спричинило зниження диференціальної ренти І на навколишніх сільськогосподарських угіддях площе 200 га на 100 грн./га, а на віддалених угіддях площею 100 га на 50 грн./га. Щорічні збитки в інших галузях склали 15000 грн. Вартість введення очисних споруд становить 1 млн. грн.., а експлуатаційні видатки на їх утримання – 120 тис. грн.. Визначити величину збитків, завданих забрудненням навколишнього середовища.

Для отримання результату задачі потрібно додати всі витрати (збитки), пов’язані із введенням в експлуатацію підприємства. Так збитки від зниження якості земельних ресурсів через втрату рентного доходу можна розрахувати:

200 га х 100 грн./га + 100 га х 50 грн./га = 25000 грн.

З урахуванням збитків в інших галузях:

25000 грн. + 15000 грн. = 40000 грн.

Будівництво очисних споруд є необхідним природоохоронним заходом, а тому витрати на їх будівництво і експлуатацію треба теж відносити на величину збитків від введення господарського об’єкту. Але тут є один момент. Оскільки всі втрати ренти і збитки у інших галузях річні, то й величину витрат на будівництво треба брати до уваги за рік. При цьому потрібно знайти приведені витрати.

40000 грн. + (120000 грн. + 0,12 х 1000000 грн.) = 280000 грн.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Частина іі.	\|	ЧАСТИНА III. ВИКОНАННЯ КПІЗ

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.