• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ймовірність суми сумісних подій

Раніше була розглянута теорема додавання для несумісних подій. Тут буде доведена теорема додавання для сумісних подій.

Дві події називають сумісними,якщо поява однієї з них не виключає появи іншої в одному і тому ж випробуванні.

Приклад 1. А - поява чотирьох очок при киданні гральної кістки; В - поява парного числа очок. Події А і В - сумісні.

Хай події А і В сумісні, причому відомі ймовірності цих подій і ймовірність їх спільної появи. Як знайти ймовірність події А+В, що полягає в тому, що з’явиться хоча б одна з подій А і В? Відповідь на це питання дає теорема додавання ймовірностей сумісних подій.

Теорема.Ймовірність появи хоча б однієї з двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх спільної появи:

.

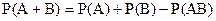Доведення. Оскільки події А і В, за умовою, сумісні, то подія А+В настане, якщо настане одна з наступних трьох несумісних подій: 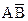, або . По теоремі додавання ймовірностей несумісних подій

. (*)

Подія А відбудеться, якщо настане одна з двох несумісних подій: 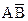або . За теоремою додавання ймовірностей несумісних подій маємо

.

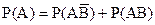Звідси

. (**)

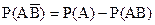Аналогічно маємо

.

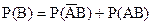Звідси

. (***)

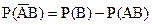Підставивши (**) і (***) в (*), остаточно одержимо

. (****)

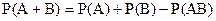Зауваження 1. При використанні одержаної формули потрібно мати на увазі, що події А і В можуть бути як незалежними, так і залежними.

Для незалежних подій

;

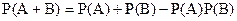для залежних подій

.

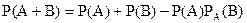Зауваження 2. Якщо події А і В несумісні, то їх суміщення є неможлива подія і, отже, 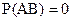. Формула (****) для несумісних подій приймає вигляд

.

Ми знову одержали теорему додавання для несумісних подій. Таким чином, формула (****) справедлива як для сумісних, так і для несумісних подій.

Приклад 2. Ймовірності влучення в ціль при стрільбі першої і другої гармат відповідно рівні: ; . Знайти ймовірність влучення при одному залпі (з обох гармат) хоча б одною з гармат.

Розв’язок. Ймовірність влучення в ціль кожною із гармат не залежить від результату стрільби з іншої гармати, тому подія А (влучення першої гармати) і В (влучення другої гармати) незалежні.

Ймовірність події (обидві гармати дали влучення)

.

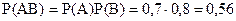Шукана ймовірність

.

Зауваження 3. Оскільки в даному прикладі події А і В незалежні, то можна було скористатися формулою . Дійсно, ймовірності подій, протилежних подіям А і В, тобто ймовірності промахів, такі:

; .

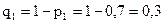Шукана ймовірність того, що при одному залпі хоча б одна гармата дасть влучення, дорівнює

.

Як і слід було очікувати, отримано той же результат.

Читайте також:

1. Алгебра випадкових подій
2. Алгебра подій
3. Безвілля, його заподій і переборення.
4. Види випадкових подій
5. Визначення базисних подій. Ідентифікація ризику.
6. Виникнення Народного Руху України за перебудову. Роль цієї організації у розвиткові політичних подій в республіці протягом 1989-1991 р.
7. Витрати від надзвичайних подій
8. Виявлення, оцінка та зменшення ризиків небезпечних подій. Облік і аналіз показників охорони праці
9. Втручання тоталітарних держав до подій в Іспанії
10. Географічні фактори, які визначають поширення паразитів та ймовірність існування певних паразитарних систем
11. Геометрична ймовірність
12. Дайте аналіз розвитку революційних подій на Україні в 1905-1907 рр.

Переглядів: 5961