• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Теорема множення ймовірностей

Розглянемо дві події: А і В, ймовірності Р(А) і Р_А(В) яких відомі. Як знайти ймовірність суміщення цих подій, тобто ймовірність того, що з’явиться і подія А і подія В? Відповідь на це питання дає теорема множення.

Теорема. Ймовірність спільної появи двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, обчислену в припущенні, що перша подія вже наступила:

.

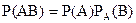Доведення. За визначенням умовної ймовірності,

.

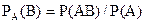Звідси

. (*)

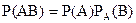Зауваження. Застосувавши формулу (*) до події ВА, одержимо

,

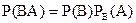чи, оскільки подія ВА не відрізняється від події АВ,

. (**)

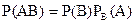Порівнюючи формули (*) і (**), робимо висновок про справедливість рівності

. (***)

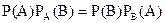Наслідок. Ймовірність спільної появи декількох подій дорівнює добутку ймовірності однієї з них на умовні ймовірності всіх інших, причому ймовірність кожної наступної події обчислюється в припущенні, що всі попередні події вже з’явились:

,

де 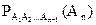- ймовірність події 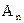, обчислена в припущенні, що події 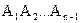наступили. Зокрема, для трьох подій

.

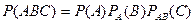Відмітимо, що порядок, у якому розташовані події, може бути обраний будь-яким, тобто байдуже яку подію вважати першою, другою і т.д.

Приклад 1. У складальника є 3 конусних і 7 еліптичних валиків. Складальник взяв один валик, а потім другий. Знайти ймовірність того, що перший з узятих валиків - конусний, а другий - еліптичний.

Розв’язок. Ймовірність того, що перший валик виявиться конусним (подія А),

.

Ймовірність того, що другий валик виявиться еліптичним (подія В), обчислена в припущенні, що перший валик - конусний, тобто умовна ймовірність

.

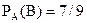За теоремою множення шукана ймовірність

.

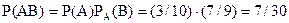Відмітимо, що, зберігши позначення, легко знайдемо: 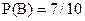, , 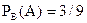, 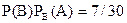що наочно ілюструє справедливість рівності (***).

Приклад 2. В урні знаходиться5 білих, 4 чорних і 3 синіх кулі. Кожне випробування полягає в тому, що навмання виймають одну кулю, не повертаючи її назад. Знайти ймовірність того, що при першому випробуванні з’явиться біла куля (подія А), при другому - чорна (подія В) і при третьому - синя (подія С).

Розв’язок. Ймовірність появи білої кулі в першому випробуванні

.

Ймовірність появи чорної кулі в другому випробуванні обчислена в припущенні, що в першому випробуванні з’явилась біла куля, тобто умовна ймовірність

.

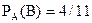Ймовірність появи синьої кулі у третьому випробуванні, обчислена в припущенні, що в першому випробуванні з’явилася біла куля, а в другому - чорна, тобто умовна ймовірність

.

Шукана ймовірність

.

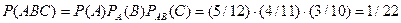Читайте також:

1. Аксіоми додавання і множення
2. Безстатеве розмноження та його біологічне значення
3. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
4. В. Друга теорема про розклад.
5. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
6. Властивості ймовірностей
7. Вступ у теорію ймовірностей
8. Додавання, віднімання, множення і ділення цілих чисел. Теореми про існування та єдиність цих операцій. Закони операцій додавання і множення.
9. Друга теорема Вейєрштрасса
10. Економіко-правові проблеми примноження національного багатства.
11. Загальна характеристика дроб’янок, їх класифікація. Ціанобактерії. Будова та форми клітин справжніх бактерій. Способи живлення і розмноження бактерій
12. Інтегральна теорема Лапласа

Переглядів: 3954