
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Математичне сподіванння дискретної випадкової величини
Математичне сподіванння, як буде показано далі, приблизно дорівнює середньому значенню випадкової величини. Для рішення багатьох задач досить зиати математичне сподіванння. Наприклад, якщо відомо, що математичне сподіванння числа оочок, що вибивають, у першого стрільця більше, ніж у другого, то перший стрілець у середньому вибиває більше оочок, чим другий, і, отже, стріляє краще другого. Хоча математичне сподіванння дає про випадкову величину значно менше відомостей, чим закон її розподілу, але для розв’язання задач, подібних наведеній й багатьох інших, знання математичного сподіванння виявляється достатнім.
Математичним сподіваннням дискретної випадкової величини називають суму добутків всіх її можливих значень на їхні імовірності.
Нехай випадкова величина X може приймати тільки значення х1, х2,..., xn ймовірності яких відповідно рівні р1, р2, …, рn. Тоді математичне сподіванння М(X) випадкової величини X визначається рівністю
 .
.
Якщо дискретна випадкова величина X приймає рахункову множину можливих значень, то
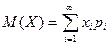 ,
,
причому математичне сподіванння існує, якщо ряд у правій частині рівності сходиться абсолютно.
Зауваження. Із визначення слідує, що математичне сподіванння дискретної випадкової величини є невипадкова (постійна) величина. Рекомендуємо запам’ятати це твердження, тому що далі воно використається багаторазово. Надалі буде показано, що математичне сподіванння безперервної випадкової величини також є постійна величина.
Приклад 1. Знайти математичне сподіванння випадкової величини X, знаючи закон її розподілу:
| X | |||
| p | 0,1 | 0,6 | 0,3 |
Розв’язок. Шукане математичне сподіванння дорівнює сумі добутків всіх можливих значень випадкової величини на їхні ймовірності:
 .
.
Приклад 2. Знайти математичне сподіванння числа появ події А в одному випробуванні, якщо ймовірність події А дорівнює р.
Розв’язок. Випадкова величина Х – число появ події А в одному випробуванні – може приймати тільки два значення: 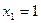 (подія А наступила) з ймовірністю р і
(подія А наступила) з ймовірністю р і 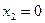 (подія А не наступило) з ймовірністю
(подія А не наступило) з ймовірністю 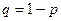 . Шукане математичне сподіванння
. Шукане математичне сподіванння
 .
.
Отже, математичне сподіванння числа появ події А одному випробуванні дорівнює ймовірності цієї події. Цей результат буде використаний нижче.
2. Ймовірнісний зміст математичного сподіванння
Нехай проведено n випробувань, у яких випадкова величина X 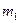 разів прийняла значення
разів прийняла значення 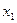 ,
, 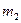 разів значення
разів значення 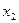 , …,
, …, 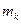 разів значення
разів значення 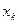 , причому
, причому 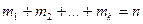 . Тоді сума всіх значень, прийнятих X, дорівнює
. Тоді сума всіх значень, прийнятих X, дорівнює
 .
.
Знайдемо середнє арифметичне 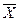 всіх значень, прийнятих випадковою величиною, для чого розділимо знайдену суму на загальне число випробувань:
всіх значень, прийнятих випадковою величиною, для чого розділимо знайдену суму на загальне число випробувань:
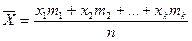
або
 . (*)
. (*)
Відмітивши, що відношення  – відносна частота
– відносна частота  значення
значення  ,
,  – відносна частота
– відносна частота 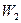 значення
значення 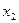 і т. д., запишемо співвідношення (*) так:
і т. д., запишемо співвідношення (*) так:
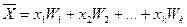 .
.
Припустимо, що число випробувань досить велике. Тоді відносна частота приблизно дорівнює ймовірності появи події (це буде доведене пізніше):
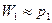 ,
, 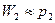 ,…,
,…, 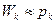 .
.
Замінивши у співвідношенні (**) відносні частоти відповідними ймовірностями, одержиимо

Права частина цієї наближеної рівності є М(Х).
Отже,
 .
.
Ймовірнісний зміст отриманого результату такий: математичне сподіванння приблизно дорівнює (тим точніше, чим більше число випробувань) середньому арифметичному спостережуваних значень випадкової величини.
Зауваження 1. Легко зрозуміти, що математичне сподіванння більше найменшого й менше найбільшого можливих значень. Іншими словами, на числовій осі можливі значення розташовані ліворуч і праворуч від математичного сподіванння. У цьому сенсі математичне сподіванння характеризує розташування розподілу й тому його часто називають центром розподілу.
Цей термін запозичений на механіки: якщо маси  ,
,  , …,
, …, 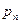 розташовані в точках з абсцисами х1, х2,..., xn, причому
розташовані в точках з абсцисами х1, х2,..., xn, причому  , то абсциса центра маси
, то абсциса центра маси
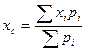 .
.
З огляду на те, що  і
і 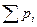 одержимо
одержимо 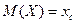 .
.
Отже, математичне сподіванння є абсциса центра маси системи матеріальних точок, абсциси яких рівні можливим значенням випадкової величини, а маси – іх ймовірностям.
Зауваження 2. Походження терміна «математичне сподіванння» пов’язане з початковим періодом виникнення теорії ймовірностей (XVI-XVII ст.), коли область її застосування обмежувалася азартними іграми. Гравця цікавило середнє значення очікуваного виграшу, або, іншими словами, математичне сподіванння виграшу.
Читайте також:
- Абсолютні і відносні величини
- Абсолютні і відносні статистичні величини
- Абсолютні, відносні та середні величини.
- Багатовимірні випадкові величини. Система двох випадкових величин
- Векторні і скалярні величини
- Векторні і скалярні величини
- Величини ліміту каси підприємства за три місяці
- Величини.
- Величини та її властивості. Дискретні випадкові величини та їх розподіли
- Видатки та заощадження як функції доходу. Автономні величини та їх чинники. Крива планових видатків.
- Визначення величини зносу направляючих.
- Визначення величини одноденних витрат окремих видів матеріальних цінностей (у натуральному і грошовому виразі).
| <== попередня сторінка | | | наступна сторінка ==> |
| ЧИСЛОВІ ХАРАКТЕРИСТИКИ ДИСКРЕТНИХ ВИПАДКОВИХ ВЕЛИЧИН | | | Властивості математичного сподіванння |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |