• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Та методи їх розв’язання.

Тема 4. Системи лінійних алгебраїчних рівнянь

Поведінка великої кількості об’єктів зовнішнього світу задовільно описується системою лінійних алгебраїчних рівнянь.

Розв’язування систем лінійних рівнянь – це одна з головних задач обчислювальної математики. Вона грає важливу роль у прикладних методах математичної статистики, економіки, міжнародних відносинах та в багатьох інших направленнях.

У загальному випадку система лінійних алгебраїчних рівнянь має вигляд

a₁₁x₁ + a₁₂x₂ +….+ a₁n_xn = b₁

a₂₁x₂ + a₂₂x₂ +….+ a₂n_xn = b₂

……………………………… (1)

a_mx₁ + a_m2x₂ +….+ a_mnx_n = b_m

Де x₁, x₂,… ,x_n - невідомі, що потрібно знайти;

a₁₁, a₁₂,…,a_mn – задані дійсні числа.

Задані числа a_ij називають коефіцієнтами системи ( i = 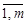, j = ).

Кожному коефіцієнту приписані індекси. Перший індекс вказує номер рівняння, у якому знаходиться даний коефіцієнт, а другий індекс – номер невідомого, перед яким цей коефіцієнт стоїть.

Числа b₁, b₂,...,b_m – називаються вільними членами системи (i = 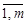), вони вважаються відомими.

Необхідно відзначити, що для будь-якої системи можливі тільки три випадки:

· система не має жодного розв’язку;

· система має єдиний розв’язок;

· система має нескінчену множину розв’язків.

Коефіцієнти при невідомих системи рівнянь, що записані у вигляді матриці А:

,

називають матрицею коефіцієнтів системи.

Якщо кількість рівнянь системи m дорівнює кількості невідомих n, то система має квадратну матрицю А порядку n. У такому випадку визначник D = det A називаються визначником системи.

Вільні члени системи, що записані у вигляді матриці-стовпця В:

B = ,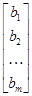

називаються вектором-стовпцем вільних членів.

Невідомі системи x₁, x₂,… ,x_n, що записані у вигляді матриці-стовпця Х:

X = ,

називаються вектором-стовпцем невідомих.

Матриця коефіцієнтів системи, доповнена справа вектором-стовпцем вільних членів, називається розширеною матрицею коефіцієнтів системи.

Така матриця має вигляд:

.

Система може бути записана у матричній формі A × Х = В

A = [A] _mxn , Х = [X] _nx1 , В = [B] _mx1 .

Якщо всі вільні члени b₁, b₂,..,b_m дорівнюють 0, то система називається однорідною, а якщо серед них є хоча б один не нульовий член, то система називається неоднорідною.

Читайте також:

1. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
2. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
3. Адаптовані й специфічні методи дослідження у журналістикознавстві
4. Адміністративні (прямі) методи регулювання.
5. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.
6. Адміністративні методи управління
7. Адміністративні, економічні й інституційні методи.
8. Адміністративно-правові (організаційно-адміністративні) методи мотивації
9. Адміністративно-правові методи забезпечення економічного механізму управління охороною довкілля
10. Аерометоди
11. Активні групові методи
12. Алгоритм розробки методичних основ бюджетування

Переглядів: 660