• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Пример 4.3

Вертикально расположенный призматический стержень (4.19) нагружен силой тяжести и сосредоточенной силой P, приложенной на свободном конце. Построить эпюры нормальных сил, напряжений и перемещений.

Нормальная сила в сечении на расстоянии x от свободного конца равна сумме силы P и силы тяжести его нижней части:

,

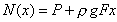РіРґРµ ПЃ - плотность материала стержня, g - ускорение СЃРІРѕР±РѕРґРЅРѕРіРѕ падения. Нормальная сила Рё нормальное напряжение Пѓ(x)=N(x)/F+ПЃgx изменяются РїРѕ линейному закону (РРёСЃСѓРЅРѕРє 4.19). Перемещение текущего сечения равно удлинению верхней части Р±СЂСѓСЃР° Рё может быть определено РїРѕ закону Гука:

.

.

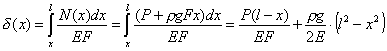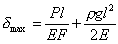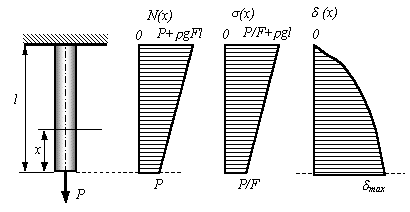
РРёСЃСѓРЅРѕРє 4.19

Анализ напряженного состояния при растяжении (сжатии)

При растяжении бруса наклонные сечения, как и поперечные, остаются плоскими и параллельными. Следовательно, внутренние силы распределены по наклонным сечениям равномерно.

Нормальное напряжение РІ поперечном сечении растянутого или сжатого стержня есть главное напряжение. Поэтому РЅР° СЂРёСЃСѓРЅРѕРє 4.20 РѕРЅРѕ обозначено s₁. Так как отлично РѕС‚ нуля только РѕРґРЅРѕ главное напряжение, то напряженное состояние РїСЂРё РѕРґРЅРѕРѕСЃРЅРѕРј растяжении (сжатии) является линейным. РџСЂРё растяжении:

,

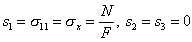при сжатии:

.

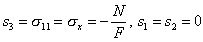Составляющие вектора полного напряжения по координатным осям в наклонной площадке определяются из уравнения (3.9) или (3.10):

,

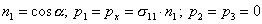Нормальные и касательные напряжения в наклонной площадке – по уравнениям (3.12), (3.13). Для случая растяжения стержня:

,

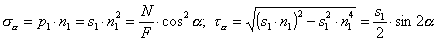На площадке, наклоненной под углом β=π/2+α:

,

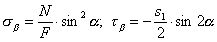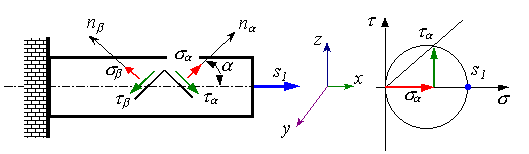
РРёСЃСѓРЅРѕРє 4.20. Напряжения РЅР° наклонных площадках

РќР° 4.20 показаны напряжения РЅР° наклонных площадках Рё построен РєСЂСѓРі РњРѕСЂР° для случая растяжения стержня. Аналогичные построения Рё расчеты РјРѕРіСѓС‚ быть сделаны Рё для случая сжатия стержня. Таким образом, напряжения РІ стержне изменяются РІ зависимости РѕС‚ наклона сечения. Тем самым РЅР° конкретном примере подтверждается зависимость напряжений РІ точке тела РѕС‚ ориентировки площадки РёС… действия. Анализ формул показывает, что РїСЂРё РѕРґРЅРѕРѕСЃРЅРѕРј растяжении Р±СЂСѓСЃР° нормальные напряжения достигают наибольших значений РІ поперечных сечениях (О±=0), Р° касательные напряжения П„_О± - РІ сечении, наклонном Рє РѕСЃРё Р±СЂСѓСЃР° РїРѕРґ углом О±=45В°, причем П„_max=s₁/2. Р’ продольном сечении (О±=90В°) касательные Рё нормальные напряжения равны нулю.

Р?нтересно отметить, что СЃСѓРјРјР° нормальных напряжений РЅР° РґРІСѓС… любых ортогональных площадках есть величина постоянная, Р° касательные напряжения РЅР° этих площадках равны РїРѕ величине, что является проявлением сформулированного выше закона парности касательных напряжений.

Читайте також:

1. Пример 10.2
2. Пример 10.3
3. Пример 12.1
4. Пример 12.2
5. Пример 12.3
6. Пример 12.5
7. Пример 12.6
8. Пример 13.1
9. Пример 13.2
10. Пример 15.2
11. Пример 15.3
12. Пример 3.1

Переглядів: 549