• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Формула складного відсотка

Нехай на початкове число K нараховується складний відсоток за певною нормою протягом п років. Тоді дістанемо таку послідовність сум:

після 1-го року: K₁ = K + Ki = K(1 + i);

після 2-го року: K₂ = K₁ + K₁i = K₁(1 + i) = K(1 + i)²;

………………………………………………………………...…

після n-го року: K_n = K_n-1 + K_n-1(1 + i) = K_n-1(1 + i) = K(1 + i)ⁿ.

Остаточна (кінцева) сума K_n при нарахуванні складного відсотка протягом n років становить K(1 + i)ⁿ.

Основна формула складного відсотка:

Якщо складний відсоток нараховується протягом п років, виконується така залежність:

Вираз 1 + і = r називається коефіцієнтом складного відсотка.

Приклад.До ощадного банку зроблено внесок на суму 100 000 грн. Яку суму сплатить ощадний банк через 10 років, якщо відсоткова ставка р дорівнює 3%?

· Задано K = 100 000; р = 3%; n = 10. Потрібно обчислити K_n.

Згідно з (14) маємо: K₁₀ = 100 000 (1 + 0,03)¹⁰ = 134 392. ·

5. Економічна задача. Дисконтування

Означення. Обчислення початкової суми за відомим її кінцевим значенням називається дисконтуванням. Різниця D між кінцевою сумою K_n та сумою K, що дисконтується, називається дисконтом:

Якщо грошові кошти K вкладати під прості відсотки на п років за питомої відсоткової ставки і, то остаточна сума буде така:

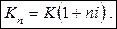
Отже, дисконтовані грошові кошти становитимуть: .

У разі складних відсотків маємо: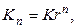

а дисконтоване значення грошової суми .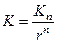

Коефіцієнт 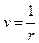називається коефіцієнтом дисконту.

Зауваження. На практиці для полегшення обчислень користуються таблицями, де задано значення коефіцієнтів дисконту для відповідних норм відсотка та кількості років.

Приклад.Які грошові кошти потрібно внести до ощадної каси, щоб за умови 3% річних одержати через 10 років суму 200 000 грн.?

· Коефіцієнт дисконту в десятому степені в разі 3% річних такий:

Отже, дисконтована сума становить K = 200 000 · 0,74409=148 818 грн.·

Зауваження. Якщо немає таблиць коефіцієнтів дисконту, можна скористатися таблицями логарифмів. Тоді lgK = lg 200 000 – 10 lg 1,03.

Звідси K = 148 818 грн.

Читайте також:

1. Абсолютні й відносні посилання у формулах
2. Барометрична формула
3. Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі
4. Визначення виробничого циклу складного процесу
5. Втрати енергії вздовж круглого трубопроводу. Формула Пуазейля і коефіцієнт Дарсі.
6. Загальна формула для визначення переміщень. Метод Мора
7. Загальна формула руху капіталу
8. Інтерполяційна формула Лагранжа.
9. Іякщо функція (4.24) є розв'язною відносно диференційого рівняння (4.2) при всіхзначеннях c1,…,cn, які визначяються формулами (4.26), коли т.(x,y,y`,…,y(n-1)).
10. Кредит — це система відносин з приводу акумуляції та використання тимчасово вільних грошових засобів на основі повернення та платності у формі позичкового відсотка.
11. Ламінарна течія рідин та газів по трубах. Формула Пуазейля
12. Лейкоцитарна формула у здорових людей

Переглядів: 1036