• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рівняння нерозривності (суцільності) потоку

Встановимо загальну залежність між швидкостями в потоці рідини, для якої дотримується умова суцільності, або нерозривності руху, тобто не утворюється пусток, не заповнених рідиною.

Виділимо усередині потоку елементарний паралелепіпед об'ємом dV = dxdxdz, ребра якого орієнтовані паралельно осям координат (рис.16).

Рис. 16. До виведення диференціального рівняння нерозривності потоку.

Припустимо, що складова швидкості потоку уздовж осі х в точках, що лежать на лівій грані паралелепіпеда площею dS = dydz, дорівнює ω_x. Тоді, згідно рівнянню (2.2), через цю грань в паралелепіпед увійде уздовж осі х за одиницю часу маса рідини ρω_xdydz, а за проміжок часу dτ – маса рідини

G_x = ρω_xdydzdτ,(2.10)

де ρ – густина рідини на лівій грані паралелепіпеда.

На протилежній (правої) грані паралелепіпеда швидкість і густина рідини можуть відрізнятися від відповідних величин на лівій грані і будуть дорівнювати 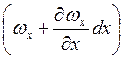і 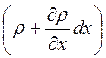. Тоді через праву грань паралелепіпеда за той самий час dτ вийде маса рідини

. (2.11)

Прирощення маси рідини в паралелепіпеді уздовж осі х:

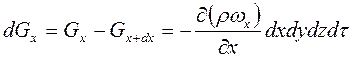. (2.12)

Якщо складові швидкості уздовж осей у і z дорівнюють ω_y і ω_z відповідно, то прирощення маси в елементарному об'ємі уздовж цих осей аналогічно складуть:

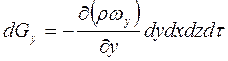і .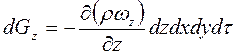

Загальне накопичення маси рідини в паралелепіпеді за час dτ дорівнює сумі її прирощень уздовж усіх осей координат:

. (2.13)

Разом з тим зміна маси у повністю заповненому рідиною об'ємі паралелепіпеда можлива тільки внаслідок зміни густини рідини в цьому об'ємі. Тому

.

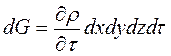Прирівнюючи (2.13) і (2.14), скорочуючи на (– dxdxdz) і переносячи в ліву частину рівняння, остаточно одержимо

. (2.14)

Рівняння (2.14) є диференціальним рівнянням нерозривності потоку для несталого руху рідини, що стискається.

Рівняння (2.14) може бути записане і в дещо іншій формі. Проводячи диференціювання добутків ρω, одержимо

,

або

,

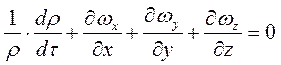де 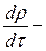субстанціональна похідна густини.

Субстанціональна похідна характеризує зміну будь-якого параметру або властивості матерії (субстанції) в часі при переміщенні матеріальних частинок у просторі.

У сталому потоці густина не змінюється в часі, тобто = 0, і рівняння (2.14) набуває вигляду:

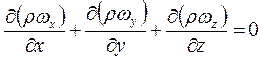. (2.15)

Для краплинних рідин, які практично не стискаються, а також для газів в умовах ізотермічного потоку при швидкостях, значно менших швидкості звуку, ρ=const і, отже,

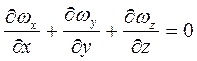. (2.16)

Рівняння (2.16) є диференціальним рівнянням нерозривності потоку рідини, що не стискається.

Сума змін швидкості уздовж осей координат в лівій частині рівняння (2.16) називається дивергенцією вектора швидкості і позначається через div ω. Тому дане рівняння можна представити як

.

Для того, щоб перейти від елементарного об'єму до всього об'єму рідини, яка рухається суцільним потоком (без розривів і пусток) по трубопроводу змінного перерізу (рис.17), проінтегруємо диференціальне рівняння (2.15).

Якби площа перерізу трубопроводу не змінювалася, то для сталого однонаправленого руху (у напрямку осі х) інтегрування рівняння (2.15) дала б залежність

ρω = const,

де ω – середня швидкість рідини.

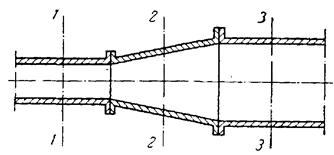
Рис. 17. До виведення рівняння сталості витрати

Якщо ж площа перерізу S трубопроводу змінна, то, інтегруючи також за площею, одержимо

ρω S = const . (2.17)

Для трьох різних перерізів (1-1, 2-2 і 3-3) трубопроводу, зображеного на рис.17, маємо

, (2.18)

або

G₁ = G₂ = G₃,

де G = ρωS – масова витрата рідини, кг/с.

Вираження (2.17) або (2.18) є рівнянням нерозривності (суцільності) потоку в його інтегральній формі для сталого руху. Це рівняння називається також рівнянням постійності витрати. Згідно рівнянню постійності витрати, при сталому русі рідини, що повністю заповнює трубопровід, через кожний його поперечний переріз проходить в одиницю часу одна і та ж сама маса рідини.

Для краплинних рідин ρ₁ = ρ₂ = ρ₃= const, тоді рівняння (2.17) набуває вигляду:

ωS = const. (2.19)

Отже,

ω₁S₁= ω₂S₂ = ω₃S₃ = const, (2.20)

або

Q₁ = Q₂ = Q₃ , (2.21)

де Q = ωS – об'ємна витрата рідини, м³/с.

З рівняння (2.20) виходить, що швидкості краплинної рідини в різних поперечних перетинах трубопроводу обернено пропорційні площам цих перетинів.

Згідно рівнянню (2.17), масова витрата рідини через початковий переріз трубопроводу дорівнює її витраті через кінцевий переріз трубопроводу. Таким чином, рівняння сталості витрати є окремим випадком закону збереження маси і виражає матеріальний баланс потоку.

У деяких випадках, наприклад, при скипанні рідини внаслідок різкого зниження тиску, утворюється пара, що може призвести до розриву потоку. В таких умовах, які іноді мають місце при роботі насосів, рівняння нерозривності потоку не виконується.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Асимптотичний підхід до порівняння оцінок
3. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
4. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
5. Вивід основного рівняння фільтрації
6. Видаток і середня швидкість ламінарного потоку.
7. Вихідного грошового потоку
8. Властивості пуассонівського потоку
9. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
10. Географічна оцінка туристського потоку
11. Головне рівняння відцентрового насоса. Теоретичний напір.
12. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.

Переглядів: 5651