• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ПЕРЕХIДНI ПРОЦЕСИ У КОЛI RLC

Розглянемо режим вiльних коливань у послiдовному коливальному контурi (рис.3.1). Припустимо, що у попереднiй момент до короткого замикання кола, електромагнiтна енергiя зосереджена в ємностi, а струм в iндуктивностi дорiвнює нулю: , .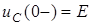

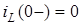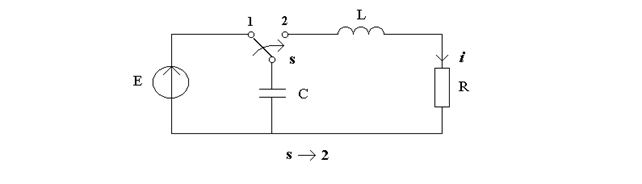
Рисунок 3.1

Щоб розв’язати задачу аналiзу вiльних коливань, складемо i розв'яжемо систему рiвнянь:

.

Пiдставивши друге рiвняння до першого, отримуємо диференцiйне рiвняння другого порядку

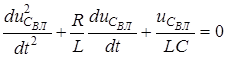, (3.1)

або ,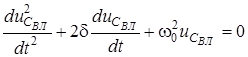

де ; 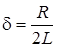- коефiцiєнт загасання.

Рiвнянню (3.1) вiдповiдає характеристичне рiвняння,

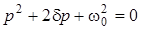, (3.2)

яке має два коренi ,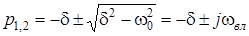

де - кутова частота незатухаючих коливань (резонансна частота);

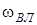- кутова частота власних (вiльних) загасаючих коливань.

Залежно вiд параметрiв кола можливi три основних режими:

1) коренi 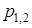- дiйснi рiзнi. При цьому 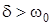, , 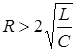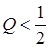(аперiодичний режим вiльних коливань);

2) коренi 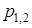- дiйснi рiвнi (кратнi). При цьому 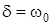, , 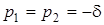, 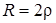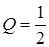(критичний режим);

3) коренi 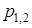- комплексно-спряженi. При цьому 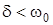, , 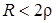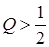(коливальний режим).

Отже, вiд вигляду коренiв характеристичного рiвняння залежить характер вiльних коливань в контурi.

1. Аперiодичний режим.

Якщо коренi 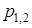- рiзнi (варiант 1 i 3 ), тобто не утворюють кратного кореня, то, як вiдомо, загальний розв’язок (3.1) записується у виглядi

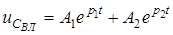. (3.3)

Для визначення струму у колi скористаємось спiввiдношенням : .

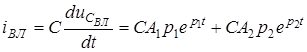Для визначення 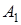та 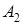, пiдставимо 0+ до останнiх двох виразiв:

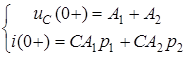. (3.4)

З урахуванням початкових умов 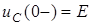, 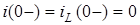., а також законiв комутацiї, матимемо

; .

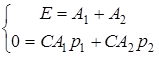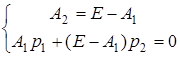З цiєї системи отримаємо: 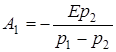; 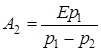. Пiдставивши значення 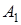i 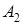до (3.3), маємо

; (3.5)

.

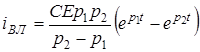Оскiльки , то . (3.6)

Оскiльки 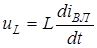, . (3.7)

Графiки, якi побудованi згiдно з (3.5)-(3.7), зображено на рис.3.2а-в. Цi графiки вiдповiдають випадку, коли обидва коренi вiд'ємнi, а другий корiнь 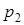за абсолютною величиною бiльше першого. Струм буде максимальним при .

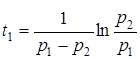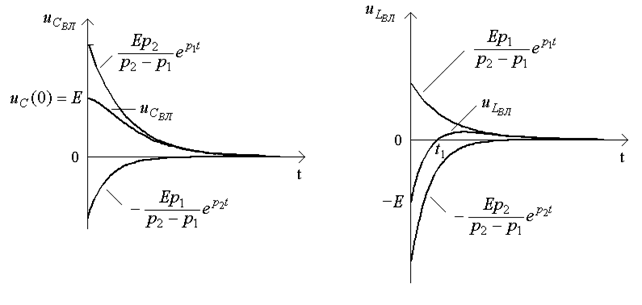
а) б)

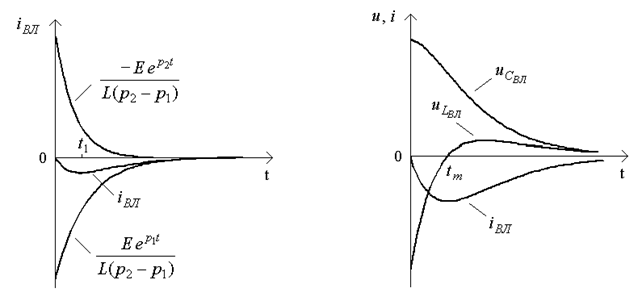
в) г)

Рисунок 3.2

2. Критичний (граничний аперiодичний) режим.

На межі мiж коливальним i аперiодичним режимами знаходиться критичний режим вiльних коливань. Вiн вiдповiдає випадку кратних коренiв характеристичного рiвняння, коли 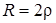, , 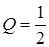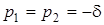. У цьому режимi 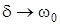, частота власних (вiльних) коливань 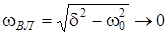, а перiод вiльних коливань .

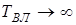Загальний розв’язок рiвняння (3.1) для кратних коренiв має вигляд

. (3.8)

Визначимо сталi iнтегрування 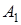і 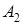з початкових умов. Пiдставимо значення 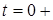до (3.8). Тодi . Друге рiвняння отримуємо з виразу ; .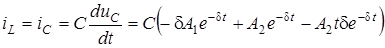

Оскiльки , , 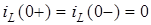то

; .

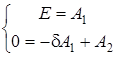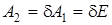Тодi 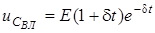; (3.9)

.

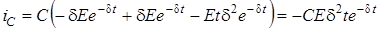Оскiльки у критичному режимi 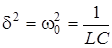, то

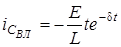; (3.10)

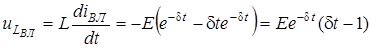. (3.11)

Кривi змiнювання напруги на ємностi та iндуктивностi i струму у колi, якi визначаються згiдно з (3.9) - (3.11), зображено на рис.3.2г. Цi залежностi аналогiчнi кривим, які зображено на рис.3.2а-в. Струм буде максимальним за абсолютною величиною при 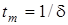. Порiвнюючи графiки, можна стверджувати, що власнi процеси у даному випадку також мають аперiодичний характер. Тобто умова 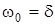є граничною умовою iснування аперiодичного процесу в контурi.

Читайте також:

1. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
2. Блок 1. Соціально-демографічні та міграційні процеси.
3. Важелі впливу на процеси розвитку ринку капіталу.
4. Виробничий, технологічний і трудовий процеси
5. Виробничі процеси, їх класифікація і принципи організації
6. Вплив нового зовнішньополітичного мислення, американо-радянського співробітництва на світові процеси
7. Вплив опромінення на процеси старіння
8. Вплив рослин та тваринних організмів на процеси переносу
9. Вплив світових фінансових криз на процеси глобалізації.
10. Вплив суб’єктивних факторів на процеси управління ризиком
11. Геодинамічні процеси у озерах і болотах
12. Геологічні процеси і явища

Переглядів: 2015