• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Ізоморфізм множин

Приклад частково впорядкованої множини показаний на мал. 1.10 (у якості відношення розглянуте відношення включення ). У цьому прикладі пари елементів: {y} і {x}, {y} і {a}, {x} і {a}, {y,x} і {y,a}, {y,x}і {a,x}, {y,a} і {a,x}, {y} і {a,x}, {a} і {y,x} непорівнянні. Інші елементи попарно порівнянні. Рис. 1.10

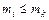Для елементів елемент називають верхньою гранню, якщо й .

Для елементів елемент 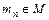називають нижньою гранню, якщо й .

Для деяких елементів m_i і m_j верхні або нижні грані можуть не існувати або бути не єдиними.

Найменша верхня грань - менша із всіх верхніх граней.

Найбільша нижня грань - більша із всіх нижніх граней.

Частково впорядковану множину можна зобразити у вигляді діаграми. Мовою діаграм два елементи перебувають у відносинах впорядкованості, тобто 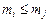, якщо існує шлях зі стрілок, що веде з m_i до m_j; верхня грань елементів m_i і m_j – це елемент, до якого є шлях з m_i і з m_j; нижня грань елементів m_i і m_j – це елемент, з якого є шлях до m_i і до m_j.

Прикладом частково впорядкованої множини, представленої у вигляді діаграми, є мал. 1.10.

Відношення називають оберненим до R, якщо тільки тоді, коли .

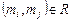Принцип подвійності: відношення, обернене до відношення впорядкованості – відношення упорядкованості.

Двоїстою до частково впорядкованої множини М є частково впорядкована множина , визначена на тім же носії за допомогою оберненого відношення. На рис.1.11 показані двоїсті діаграми частково впорядкованих множин.

Ланцюг у М – це лінійно впорядкована підмножина впорядкованої множини М.

Довжина ланцюга - це число 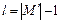, де - потужність носія.

Висота d(m_i) елемента m_i упорядкованої множини М - максимум довжини ланцюгів m₀ < m₁ < m₂ < … < m_i у М, для яких m_i – найбільший елемент (т₀ – мінімальний елемент множини М).

Рис. 1.11

Довжина d(М ) упорядкованої множини М - максимум довжин ланцюгів у М або максимум висот d_i(m_i) його елементів: .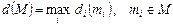

§ 7. РЕШІТКИ (СТРУКТУРИ). ІЗОМОРФІЗМ. ДЕДЕКИНДОВІ ТА ДИСТРИБУТИВНІ РЕШІТКИ

Структура–відношення, що задовольняє аксіомам структури. Часто під структурами розуміють решітки.

Решітка(структура) - частково впорядкована множина, у якій будь-які два елементи m_i, m_j мають єдину найбільшу нижню грань, або перетинання , і єдину найменшу верхню грань, або об'єднання 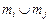(Упорядкована множина не є решіткою, коли: якісь два елементи не мають верхньої або нижньої грані або для деякої пари елементів найменша верхня (або найбільша нижня) грань неєдина. Упорядкована множина , двоїста решітці М, є решіткою, у якій перетинання й об'єднання міняються ролями).

Решітка є алгеброю , сигнатура якої має властивості:

1. (ідемпотентність);

2. (комутативність);

3. 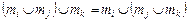, 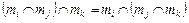(асоціативність);

4. , (поглинання).

де - операція узяття найменшої верхньої грані елементів (об'єднання); - операція узяття найбільшої нижньої грані елементів (перетинання ).

Решітка повна (повна структура), якщо перетинання й об'єднання існують для будь-якої підмножини її елементів.

Максимальний елемент решітки (одиниця решітки (структури)) – це об'єднання всіх елементів повної решітки (повної структури).

мінімальний елемент решітки (нуль решітки (структури)) – це перетинання всіх елементів повної решітки (повної структури).

Підрешітка решітки А - підмножина решіток А, що разом з кожною парою елементів т_i і m_j містить також 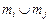і .

Інтервал I , визначений елементами й у решітці А, - це підрешітка решітки А з найменшим елементом і найбільшим елементом :

У решітці А зі структурними нулем і одиницею два елементи й називають додатковими, якщо й .

Елемент , додатковий до т , називається також доповненнямелемента т у решітці А.

Два елементи, що володіють загальним доповненням у решітці А , називають зв'язанимив А.

Ізоморфізм властивість однаковості будови сукупностей елементів.

Множини М, М* ізоморфні, якщо існує взаємно однозначна відповідність 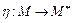така, що для найдеться 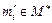такий, що й існує обернена взаємно однозначна відповідність така, що для найдеться такий, що .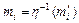

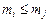Упорядковані множини М, М* ізоморфні , якщо між ними існує ізоморфізм, що зберігає порядок, тобто існує взаємно однозначна відповідність між М і М*, коли із виходить й навпаки: ізвиходить .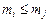

Приклад. □ Будь-які дві алгебри множин, утворені різними множинами U і U* однакової потужності, ізоморфні: операції в них просто однакові, а відображенням може служити будь-яка взаємно однозначна відповідність між U і U*:

Поняття ізоморфізму є одним з найважливіших понять у математиці. Його суть можна виразити в такий спосіб : якщо алгебри А и А* ізоморфні, то елементи й операції в алгебрі А* можна перейменувати так, що А* збіжиться з А. З умови ізоморфізму витікає, що, наприклад, будь-яке еквівалентне співвідношення в алгебрі А зберігається в будь-якій ізоморфній їй алгебрі. Це дозволяє, одержавши такі співвідношення в алгебрі А, автоматично поширити їх на всі алгебри, ізоморфні А. Вираження “розглядати об'єкти з точністю до ізоморфізму” означає, що розглядаються тільки ті властивості об'єктів, які зберігаються при ізоморфізмі, тобто є загальними для всіх ізоморфних об'єктів. Зокрема, ізоморфізм зберігає асоциативність, комутативність і дистрибутивність.

Читайте також:

1. Алгебра множин
2. Бюджетні множини й лінії бюджетного обмеження
3. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
4. Визначення множини допустимих планів задачі ЛП
5. Визначення суми на множині цілих невід’ємних чисел, її існування та єдиність. Операція додавання та її основні властивості (закони).
6. Відмінок Однина Множина
7. Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.
8. Відношення порядку на множині дійсних чисел.
9. Відношення порядку на множині невід’ємних раціональних чисел.
10. Відношення порядку на множині цілих невід’ємних чисел.
11. Властивості множини невід’ємних раціональних чисел.
12. Властивості множини цілих чисел.

Переглядів: 1607