• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Диз’юнктивна і кон’юнктивна нормальні форми

Означення.Елементарною кон’юнкцією від змінних називається кон’юнкція деяких із змінних або їх заперечень.Формулу, яка зображає елементарну кон’юнкцію будемо позначати .

Приклад. Нехай задані змінні . Елементарними кон’юнкціями від них будуть, наприклад, такі:

; ; .

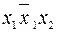Вирази , не є елементарними кон’юнкціями: в першому виразі є спільне заперечення, а в другому є знак .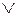

Означення. Диз’юнктивною нормальною формою (ДНФ) називається диз’юнкція елементарних кон’юнкцій (у виродженому випадку це може бути одна кон’юнкція), тобто вираз вигляду

,

де всі 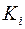, 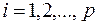– елементарні кон’юнкції (не обов’язково різні).

Приклад ДНФ..

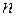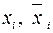Означення. Елементарна кон’юнкція від змінних називається повною, якщо до неї від кожної пари , , входить тільки одна змінна.

Приклад. Утворимо всі повні елементарні кон’юнкції від змінних :

, ,

, ,

, ,

, .

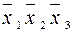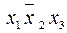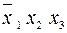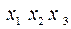Двоїстим чином, тобто з використанням принципу двоїстості, визначається поняття кон’юктивної нормальної форми.

Означення.Елементарною диз’юнкцією від змінних називається диз’юнкція деяких із змінних або їх заперечень. Формулу, яка зображає елементарну диз’юнкцію будемо позначати .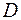

Приклад. Нехай задані змінні . Елементарними диз’юнкціями від них будуть, наприклад, такі:

; ; .

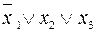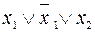Означення. Кон’юнктивною нормальною формою (КНФ) називається кон’юнкція елементарних диз’юнкцій (у виродженому випадку це може бути одна диз’юнкція), тобто вираз вигляду

,

де всі 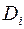, , 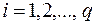– елементарні диз’юнкції (не обов’язково різні).

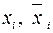Означення. Елементарна диз’юнкція від змінних називається повною, якщо до неї від кожної пари , входить тільки одна змінна.

Приклад. Утворимо всі повні елементарні диз’юнкції від змінних :

, ,

, ,

, ,

, .

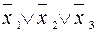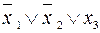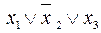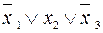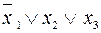Приклад КНФ. .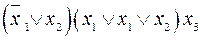

Теорема. Для кожної формули, що реалізує булеву функцію, існує рівносильна їй диз'юнктивна нормальна форма (ДНФ) і кон'юнктивна нормальна форма (КНФ).

Доведення теореми полягає просто у наведенні алгоритмів знаходження для будь-якої формули рівносильних їй ДНФ і КНФ. Процес знаходження цих форм називається приведенням формули відповідно до ДНФ і КНФ.

Читайте також:

1. А/. Форми здійснення народовладдя та види виборчих систем.
2. Автоматизовані форми та системи обліку.
3. Аграрні реформи та розвиток сільського госпо- дарства в 60-х роках XIX ст. — на початку XX ст.
4. Акредитив та його форми
5. Активні форми участі територіальної громади у вирішенні питань ММС
6. Асимптотична нормальність й ЦПТ
7. Банківський контроль та нагляд: форми та мета здійснення. Пруденційний нагляд: поняття, органи та мета проведення.
8. Батьки мають право обирати форми та методи виховання, крім тих, які суперечать закону, моральним засадам суспільства.
9. Безособові дієслівні форми на –но, -то
10. Безробіття: суть, причини, форми та соціально-економічні наслідки
11. Білінійні і квадратичні форми в евклідовому просторі
12. Бланки, форми і штампи

Переглядів: 5681