Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Напруження і деформації

РОЗТЯГАННЯ І СТИСКАННЯ

Центральний (осьовий) розтяг або стиск виникає від сил, прикладених до осі бруса (рисунок 2.1). Напружений стан, що спричиняється такими силами, називають простим або лінійним (одновісним). В силу гіпотези плоских перерізів напруження по перерізу розподіляються рівномірно, що може бути виражено формулою

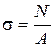, (2.1)

де - нормальне напруження в поперечному перерізі;

N- зусилля в цьому перерізі;

A- площа перерізу.

Рисунок 2.1

В різних перерізах одного і того ж бруса внутрішні зусилля N різні. При розрахунках необхідно знати внутрішні зусилля в будь-якому перерізі. Тому будують графіки N(x), з яких видно, як змінюються внутрішні зусилля N вздовж осі бруса. Такі графіки називають епюрами внутрішніх зусиль. Розглянемо східчастий брус, затиснутий лівим кінцем (рисунок 2.1), вздовж осі якого діють активні сили P i 3P. Частини бруса сталого перерізу, що містяться між площинами, в яких прикладені активні або реактивні сили, називаються ділянками. Таким чином межами ділянок є точки прикладання зовнішніх сил, а також

місця зміни розмірів поперечного перерізу. Даний брус (рисунок 2.1)складається з трьох ділянок.

Для побудови епюри повздовжньої сили N використаємо метод перерізів і рівняння рівноваги (1.4). Розтяжні (направлені від перерізу) повздовжні сили вважатимемо додатними, а стисківні (направлені до перерізу) - від’ємними. Зробимо переріз 1-1. В усіх точках перерізу діятимуть внутрішні розподілені сили, рівнодійна яких N₁, визначається з умови рівноваги однієї з частин бруса, наприклад, правої

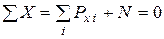Звідки N₁=P

Повздовжня сила - це рівнодійна внутрішніх нормальних сил, які виникають у поперечному перерізі. Знаходимо величину повздовжньої сили в перерізі 2-2.

, , .

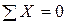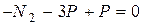Таким чином, повздовжня сила в поперечному перерізі бруса чисельно дорівнює алгебраїчній сумі зовнішніх сил, що діють з одного боку перерізу.

Для побудови епюри повздовжньої сили N під рисунком бруса проведемо лінію, паралельну осі бруса. Ця лінія називається базовою (рис. 2.1). Величини повздовжніх сил у довільному масштабі відкладемо перпендикулярно до базової лінії, причому додатні значення (розтягання) відкладемо вгору, а від’ємні (стискання) - вниз від базової лінії. Епюру штрихуємо тонкими лініями перпендикулярними до осі. У точках прикладання зосереджених сил на епюрі N мають місце стрибкоподібні зміни, причому величина “стрибка” дорівнює модулю прикладеної в перерізі бруса зовнішньої зосередженої сили (рисунок 2.1).

Очевидно, що значення ординати епюри повздовжніх сил під закріпленням дорівнює реакції закріплення. Зазначимо, що за методом перерізів зручніше розглядати рівновагу частини бруса, розміщеної з боку вільного кінця, у протилежному випадку потрібно заздалегідь визначити і вводити в рівняння рівноваги реакцію закріплення.

Щоб побудувати епюру s, визначимо за формулою (2.1) нормальні напруження на ділянках бруса, беручи значення N із епюри N(x). Тоді на першій, другій і третій ділянках будемо мати

Правила побудови епюри s(x) такі самі, як і для епюри N(x), включаючи і правило знаків. У межах кожної ділянки напруження сталі, тому епюра s(x) на кожній ділянці паралельна осі (рисунок 2.1).

У розрахунках на міцність привертають особливу увагу ті перерізи бруса, в яких напруження за абсолютними значеннями максимальні. Ці перерізи можуть бути небезпечними. У розглянутому прикладі небезпечними є перерізи бруса на 2-й ділянці.

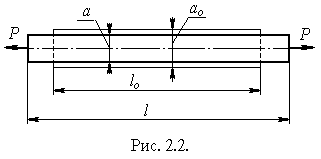
Перейдемо до розгляду деформацій. Уявимо прямий брус сталого поперечного перерізу A₀ і довжиною l₀ (рисунок 2.2). Під дією сили P брус видовжиться на деяку величину D l

(2.2)

яку називають абсолютним видовженням.

При розтяганні бруса його поперечні розміри зменшуються. При цьому абсолютна поперечна деформація дорівнюватиме

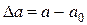. (2.3)

Відношення абсолютного видовження D l до початкової довжини l₀називають відносним видовженням і позначають e

. (2.4)

Рисунок 2.2

Аналогічно, відносна поперечна деформація дорівнює

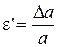. (2.5) Зв’язок між відносною поперечною і відносною повз-

довжньою деформаціями виражається формулою

, (2.6)

де m - безрозмірний коефіцієнт поперечної деформації - коефіцієнт Пуассона. Знак “мінус” у формулі (2.6) говорить про те, що деформації 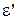і e мають різні знаки, а коефіцієнт Пуассона визначається за формулою

. (2.7)

Величина m для різних матеріалів не однакова: так, для сталі m=0.25-0.3, для каучуку m=0.47. Значення m для різних матеріалів приводяться в довідниках.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Напруження в перерізі	\|	Закон Гука при розтяганні і стисканні

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.