Парабола та її рівняння

Означення7. Параболою називається множина точок площини, однаково віддалених від заданої точки, що називається фокусом і від заданої прямої, що називається директрисою.

Виходячи з означення 7, виведемо рівняння параболи. Нехай пряма AB є директрисою параболи, а точка F є її фокусом (мал.61). Проведемо через точку F пряму перпендикулярну до директриси AB і візьмемо цю пряму за вісь абсцис,а за вісь ординат вієьмемопряму перпендикулярну до вісі абсцис і яка проходить через точку O,середину відрізка CF.Довжину відрізка CF позначимо через p

у (p>0).Координати фокуса будуть

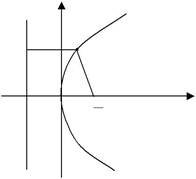
B

M

D

^C ⁰ F( ₂^p ,0)

A

( ^p ,0 ) ,а рівняння директриси AB

2

є x = − ^p. Нехай точка M(x,y) є

2

_хдовільною точкою параболи. Опу-стимо із точки M перпендикуляр на директрису AB в точці D і спо-

лучимо точку M з фокусом F. Тоді _Мал_.61 за означенням 7 маємо, що DM=MF Точка D має координати

( − p , y ). За формулою віддалі між двома точками знаходимо

( x + p )² + ( y − y )² = ( x − p )² + ( y − 0 )² .

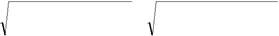Це і буде рівняння параболи відносно вибраної системи коор-динат. Підносячи обидві частини даного рівняння до квадрату, і спростивши, одержимо

y² = 2 px . (2.142)

Рівняння (2.142) і є канонічним рівнянням параболи. Як видно з рівняння (2.142) парабола є лінія другого порядку і всі її точки ро-зташовані праворуч від осі 0 y . Парабола проходить через початок

координат. Розв’язавши рівняння (2.142) відносно y , одержимо

y = ± 2 px . (2.143)

Так як p > 0 , то y буде дійсною величиною тільки тоді, коли

x додатні,а коли p < 0 , то парабола визначена для x ≤ 0 .

Із (2.143) видно, що кожному значенню x відповідає два зна-чення y , які рівні за абсолютною величиною, але протилежні за

знаком.

Значить вісь 0 x є віссю симетрії для параболи. Точку O( 0 ,0 ) називають вершиною параболи.

Якщо x необмежено зростає, то і y необмежено зростає. Вели-чина р називається параметром параболи і при збільшенні р парабо-ла розширюється, тобто її точки будуть віддалятися від осі Ох.

Якщо рівняння параболи має у

вигляд y²=−2px то вершина параболи

y² =−2 px

знаходиться в початку координат,

вісь симетрії є вісь абсцис, але пара-

бола розміщена зліва від осі Oy O х

(мал.62), а директриса такої парабо-

ли буде розміщена праворуч від осі

ординат, а фокус F ( − p ,0 ) буде Мал.62

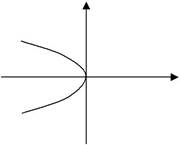ліворуч від початку координат.

Якщо директриса параболи паралельна вісі абсцис , а фокус знаходиться на вісі ординат, то рівняння параболи має вигляд

x²=±2py. (2.144)

Парабола (2.144) зображена на мал.63. Це парабола симетрична відносно осі Oy і розміщена над віссю абсцис, якщо в

у рівнянні взяти знак (+) і під віссю аб-сцис, якщо взяти знак (-).

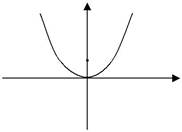Якщо в рівнянні (2.144) позна-

F чити ± = a ,то одержимо рівняння

O B 2 p

параболи y = ax² ,яку вивчають в

A

Мал.63 середній школі.

Приклад 5.Ферми,які підтримують залізнодорожний містдовжиною 112 м, мають вигляд параболи, яка задається рівнянням

y = ax² . Знайти рівняння відповідної параболи,якщо найбільша

висота мостової арки складає 44м.

Розв’язування. Візьмемо за початок координат вершину фер-ми. Тоді симетричні точки в основі ферми будуть мати координати (-56,-44) і (56,-44). Підставляючи будь-яку пару координат в рівнян-

Мал.64

ня y = ax² , одержимо − 44 = a ⋅ 3136 . Звідси a = − ⁴⁴ = − ¹¹ .

3136787

Таким чином, мостова ферма має вигляд параболи

y =− ¹¹ x² .

784

Читайте також:
V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
Асимптотичний підхід до порівняння оцінок
Бюджетний контроль - це порівняння показників бюджету зі звітом за відповідний період часу.
В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
Вивід основного рівняння фільтрації
Використання рівняння номінальних витрат за моделлю COCOMO II
ВПРАВА 2. Утворіть де можливо, форми ступенів порівняння від поданих прикметників.
Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
Гіпербола та її рівняння
Головне рівняння відцентрового насоса. Теоретичний напір.
Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.
Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.

Переглядів: 6378

<== попередня сторінка | наступна сторінка ==>

Мої l прямує до нуля при необмеженому віддалені точки M від початку координат вздовж кривої ( k ) в тому чи іншому напрямі | Перетворення прямокутних координат

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.