
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Постановка завдання статистичного дослідження
Кореляційно-регресійний аналіз взаємозв'язку ознак є складовою частиною статистичного дослідження діяльності 30-ти банків і частково використовує результати ЛР-1.
У ЛР-2 вивчається взаємозв'язок між факторною ознакою Вартість активів (ознака Х) і результативною ознакою Фінансовий результат (ознака Y), значеннями яких є початкові дані ЛР-1 після виключення з них аномальних спостережень.
| Назва банку | Вартість активів, млн.грн. | Фінансовий результат, млн. грн. |
| IНДУСТРIАЛБАНК | 3217,32 | 10,440 |
| ДIАМАНТБАНК | 3433,31 | 2,888 |
| КЛIРИНГОВИЙ ДIМ | 3516,49 | 37,996 |
| УКРАЇНСЬКИЙ ПРОФЕСIЙНИЙ БАНК | 3524,30 | 48,093 |
| СОЮЗ | 3685,43 | 2,851 |
| ПЛАТИНУМ БАНК | 3697,02 | 6,119 |
| АВАНТ - БАНК | 3759,72 | 0,438 |
| МАРФIН БАНК | 4126,06 | 1,151 |
| ДIВI БАНК | 4150,63 | 4,295 |
| АКТАБАНК | 4290,67 | 9,760 |
| КРЕДОБАНК | 4507,78 | -61,025 |
| УКРБIЗНЕСБАНК | 4516,13 | 24,627 |
| ТЕРРА БАНК | 4551,84 | 1,662 |
| ВБР | 4741,24 | 29,760 |
| МЕГАБАНК | 4840,06 | 2,005 |
| ФІДОБАНК | 4936,85 | 91,323 |
| IНГ БАНК Україна | 11526,36 | 552,362 |
| КРЕДИТПРОМБАНК | 12216,79 | -48,866 |
| КРЕДI АГРIКОЛЬ БАНК | 13175,75 | 408,502 |
| БРОКБIЗНЕСБАНК | 16927,72 | 0,518 |
| ОТП БАНК | 20314,99 | 26,153 |
| ФIНАНСИ ТА КРЕДИТ | 22548,40 | 3,166 |
| АЛЬФА-БАНК | 25588,82 | 36,251 |
| СБЕРБАНК РОСIЇ | 27025,93 | 410,073 |
| ПУМБ | 28229,81 | 271,199 |
| ДЕЛЬТА БАНК | 29842,47 | 97,858 |
| УКРСОЦБАНК | 38829,86 | 8,072 |
| ПРОМIНВЕСТБАНК | 41318,06 | 224,766 |
У процесі статистичного дослідження необхідно вирішити ряд завдань.
1. Встановити наявність статистичного зв'язку між факторною ознакою Хі результативною ознакою Yграфічним методом.
2. Встановити наявність кореляційного зв'язку між ознаками Хі Yметодом аналітичного групування.
3. Оцінити щільність зв'язку ознак Хі Yна основі емпіричного кореляційного відношення η.
4. Побудувати однофакторну лінійну регресійну модель зв'язку ознак Хі Y, використовуючи інструмент Регресіянадбудови Пакет аналізу,і оцінити щільність зв'язку ознак Хі Yна основі лінійного коефіцієнта кореляції r.
5. Визначити адекватність і практичну придатність побудованої лінійної регресійної моделі, оцінивши:
а) значущість і довірчі інтервали коефіцієнтів а0, а1;
б) індекс детермінації R2і його значущість;
в) точність регресійної моделі.
6. Дати економічну інтерпретацію:
а) коефіцієнта регресії а1;
б) коефіцієнта еластичності КЕ;
в) залишкових величин еi.
7. Знайти найбільш адекватне нелінійне рівняння регресії за допомогою засобів інструменту Майстер діаграм.
2. Висновки за наслідками виконання лабораторної роботи[2]
Завдання 1. Встановлення наявності статистичного зв'язку між факторною ознакою Хі результативною ознакою Yграфічним методом.
Статистичний зв'язок є різновидом стохастичного (випадкового) зв'язку, при якому із зміною факторної ознаки X закономірним чином змінюється який-небудь з узагальнюючих статистичних показників розподілу результативної ознаки Y.
Висновок:
Точковий графік зв'язку ознак (діаграма розсіювання, отримана в ЛР-1 після видалення аномальних спостережень) дозволяє зробити висновок, що має місце статистичний зв'язок. Очікуваний вид зв'язку – нелінійний невизначений.
Завдання 2.Встановлення наявності кореляційного зв'язку між ознаками Хі Yметодом аналітичного групування.
Кореляційний зв'язок – найважливіший окремий випадок стохастичного статистичного зв'язку, коли під впливом варіації факторної ознаки Х закономірно змінюються від групи до групи середні групові значення  результативної ознаки Y(усереднюються результативні значення
результативної ознаки Y(усереднюються результативні значення 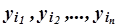 отримані під впливом чинника
отримані під впливом чинника 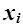 ). Для виявлення наявності кореляційного зв'язку використовується метод аналітичного групування.
). Для виявлення наявності кореляційного зв'язку використовується метод аналітичного групування.
Висновок:
Результати виконання аналітичного групування банків за факторною ознакою Вартість активів наведено в таблиці 2.2 Робочого файлу, яка показує, що із збільшенням значень факторної ознаки Хведуть себе хаотично середні групові значення результативної ознаки  . Отже, між ознаками Хі Yне можемо визначити ступінь зв’язку.
. Отже, між ознаками Хі Yне можемо визначити ступінь зв’язку.
Завдання 3.Оцінка щільності зв'язку ознак Хі Yна основі емпіричного кореляційного відношення.
Для аналізу щільності зв'язку між факторною і результативною ознаками розраховується показник η – емпіричне кореляційне відношення, що задається формулою
 ,
,
де 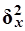 і
і  - відповідно міжгрупова і загальна дисперсії результативної ознаки Y- Фінансовий результат (індекс х дисперсії
- відповідно міжгрупова і загальна дисперсії результативної ознаки Y- Фінансовий результат (індекс х дисперсії 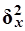 означає, що оцінюється міра впливу ознаки Хна Y).
означає, що оцінюється міра впливу ознаки Хна Y).
Для якісної оцінки щільності зв'язку на основі емпіричного кореляційного відношення служить шкала Чеддока:
| Значення η | 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Сила зв'язку | слабка | помірна | помітна | тісна | дуже тісна |
Результати виконаних розрахунків подані в таблиці 2.4 Робочого файлу.
Висновок:
Значення коефіцієнта η = 0,657, що відповідно до оцінної шкали Чеддока говорить про помітну ступінь зв'язку ознак, що вивчаються.
Завдання 4. Побудова однофакторної лінійної регресійної моделі зв'язку ознак, що вивчаються, за допомогою інструменту Регресіянадбудови Пакет аналізуі оцінка щільності зв'язку на основі лінійного коефіцієнта кореляції r.
4.1. Побудова регресійної моделі полягає в знаходженні аналітичного виразу зв'язку між факторною ознакою Xі результативною ознакою Y.
Інструмент Регресіяна основі фактичних даних (xi, yi), здійснює розрахунок параметрів а0 і а1 рівняння однофакторної лінійної регресії  , а також обчислення ряду показників, необхідних для перевірки адекватності побудованого рівняння фактичним даним.
, а також обчислення ряду показників, необхідних для перевірки адекватності побудованого рівняння фактичним даним.
Примітка. У результаті роботи інструменту Регресія отримано чотири результативні таблиці (починаючи із заданої комірки А75). Ці таблиці виводяться в Робочий файл без нумерації, тому необхідно привласнити їм номери табл. 2.5 – табл. 2.8 відповідно до їх порядку.
Висновок:
Розраховані в табл. 2.7 (комірки В91і В92) коефіцієнти а0 і а1 дозволяють побудувати лінійну регресійну модель зв'язку ознак, що вивчаються, у вигляді рівняння  .
.
4.2. У разі лінійної функції зв'язку для оцінки щільності зв'язку ознак Xі Y,що встановлюється за побудованою моделлю, використовується лінійний коефіцієнт кореляції r.
Значення коефіцієнта кореляції rнаводиться в табл. 2.5 в комірці В78 (термін "Множинний R").
Висновок:
Значення коефіцієнта кореляції r = 0,352, що відповідно до оцінної шкали Чеддока говорить про слабкий ступінь зв'язку ознак, що вивчаються.
Завдання 5. Аналіз адекватності і практичної придатності побудованої лінійної регресійної моделі.
Аналіз адекватності регресійної моделі має за мету оцінити, наскільки побудована теоретична модель взаємозв'язку ознак відображає фактичну залежність між цими ознаками, і тим самим оцінити практичну придатність синтезованої моделі зв'язку.
Оцінка відповідності побудованої регресійної моделі початковим (фактичним) значенням ознак Xі Yвиконується в 4 етапи:
1) оцінка статистичної значущості коефіцієнтів рівняння а0, а1 і визначення їх довірчих інтервалів для заданого рівня надійності;
2) визначення практичної придатності побудованої моделі на основі оцінок лінійного коефіцієнта кореляції r і індексу детермінації R2;
3) перевірка значущості рівняння регресії в цілому за F-критеріємФішера;
4) оцінка погрішності регресійної моделі.
5.1. Оцінка статистичної значущості коефіцієнтів рівняння а0, а1 і визначення їх довірчих інтервалів
Оскільки коефіцієнти рівняння а0 , а1 розраховувалися, виходячи із значень ознак тільки для 30-ти пар (xi, yi), то значення коефіцієнтів є лише наближеними оцінками фактичних параметрів зв'язку а0, а1. Тому необхідно:
1. перевірити значення коефіцієнтів на невипадковість (тобто впевнитись, наскільки вони типові для всієї генеральної сукупності комерційних банків);
2. визначити (із заданою довірчою ймовірністю 0,95і 0,683) межі, в яких можуть знаходитися значення а0, а1 для генеральної сукупності банків.
Для аналізу коефіцієнтів а0, а1 лінійного рівняння регресії використовується табл. 2.7, в якій:
– значення коефіцієнтів а0, а1 наведені в комірках В91і В92відповідно;
– розрахований рівень значущості коефіцієнтів рівняння наведений в комірках Е91і Е92;
– довірчі інтервали коефіцієнтів з рівнем надійності Р=0,95і Р=0,683вказані в діапазоні комірок F91:I92.
5.1.1. Визначення значущості коефіцієнтів рівняння
Рівень значущості – це величина α =1–Р, де Р– заданий рівень надійності (довірча ймовірність).
Режим роботи інструменту Регресіявикористовує за умовчанням рівень надійності Р=0,95.Для цього рівня надійності рівеньзначущості рівний α = 1 – 0,95 = 0,05.Цей рівень значущості вважається за заданий.
У інструменті Регресіянадбудови Пакет аналізудля кожного з коефіцієнтів а0і а1 обчислюється рівеньйого значущості αр,який вказаний у результативній таблиці (табл. 2.7 термін "Р-значення"). Якщо розрахований для коефіцієнтів а0, а1 рівень значущості αр,менше заданого рівня значущості α= 0,05, то цей коефіцієнт визнається невипадковим (тобто типовим для генеральної сукупності), інакше – випадковим.
Примітка. У випадку, якщо визнається випадковим вільний член а0, то рівняння регресії доцільно побудувати наново без вільного члена а0.У цьому випадку в діалоговому вікні Регресіянеобхідно задати ті ж самі параметри лише того, що слід активізувати прапорець Константа-нуль (це означає, що модель будуватиметься за умови а0=0). У лабораторній роботі такий крок не передбачений.
Якщо незначущим (випадковим) є коефіцієнт регресії а1,то взаємозв'язок між ознаками Xі Yв принципі не може апроксимуватися лінійною моделлю.
Висновок:
Для вільного члена а0 рівняння регресії розрахований рівень значущості становить αр = 0,5976. Оскільки він більше заданого рівня значущості α=0,05, то коефіцієнт а0 випадковим.
Для коефіцієнта регресії а1розрахований рівень значущості становить αр = 0,066 Оскільки він більше заданого рівня значущості α=0,05, то коефіцієнт а1 визнається випадковим.
5.1.2. Залежність довірчих інтервалів коефіцієнтів рівняння від заданого рівня надійності
Довірчі інтервали коефіцієнтів а0, а1 побудованого рівняння регресії при рівнях надійності Р=0,95і Р=0,683представлені в табл. 2.7, на основі якої формується табл. 2.9.
Таблиця 2.9
Читайте також:
- I. Постановка завдання статистичного дослідження
- II. Завдання на проект.
- III. Економічна інтерпретація результатів статистичного дослідження банків
- V. ДОМАШНЄ ЗАВДАННЯ
- V. ДОМАШНЄ ЗАВДАННЯ
- V. Завдання.
- VI. ДОМАШНЄ ЗАВДАННЯ
- Vi. домашнє завдання
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
| <== попередня сторінка | | | наступна сторінка ==> |
| Додаток 2 | | | Межі довірчих інтервалів коефіцієнтів рівняння |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |