• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

РІВНЯННЯ Н’ЮТОНА ТА ШВЕДОВА-БІНГАМА

Текучість звичайних нормальних рідин (води, бензолу, спирту тощо) підкоряються закону Н’ютона :

Р = η • du/dx,

де Р – напруга зсуву, що підтримує течію рідини;

η - коефіцієнт в’язкості, Па•с;

du/dx - градієнт швидкості руху, що виникає при переміщенні окремих шарів рідини, або швидкість деформації, с^-1.

Коефіцієнт в’язкості залежить від природи рідини, напруги зсуву та часу. Згідно закону Н’ютона швидкість течії рідини в ламінарному режимі збільшується пропорційно прикладеній напрузі зсуву і графічна залежність градієнта швидкості течії рідини du/dx від напруги зсуву Р – крива течії – має вигляд прямої, що проходить через початок координат.

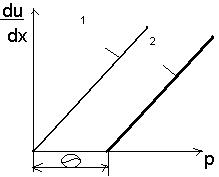
Рис. 30. Криві течії: для 1 – нормальних рідин і 2 - для структурованих систем по Шведову – Бінгаму.

& Ламіна́рна течія́ — впорядкований рух рідини, при якому рідина рухається шарами, паралельними до напрямку течії.

Для структурованих рідин ця пропорційність порушується, вони не підкоряються закону Н’ютона і тому їх називають аномальними рідинами. Якщо рахувати, що течія структурованої рідини починається тільки після повного руйнування структури, то напруга зсуву Р, що необхідна для течії, повинна бути більшою, ніж напруга зсуву Ө(межі течії), що необхідна для руйнування структури. Для характеристики течії структурованих рідин може застосовуватися рівняння Шведова – Бінгама:

Р - Ө = η• du/dx,

де Ө - межа течії;

η - в’язкість повністю зруйнованої структури – пластична в’язкість.

Для систем, що не мають просторової структури Ө = 0, рівняння Шведова – Бінгама перетворюється в рівняння Н’ютона.

За рівнянням Шведова – Бінгама залежність градієнта швидкості від напруги зсуву повинна виражатися прямою 2. І дійсно, багато структурованих систем добре підкоряються цьому рівнянню. Але для більшості структурованих систем залежність градієнта швидкості від напруги зсуву носить більш складний характер. Це пояснюється тим, що в коагуляційній структурі можуть протікати одночасно два процеси – руйнування структури і процес її відновлення.

При малих швидкостях течії структура руйнується дуже незначно, а зруйновані зв’язки швидко відновлюються. Практично в цьому випадку рідина тече без руйнування структури і в’язкість її постійна і досить велика. Це явище називається повзучістю. При дуже великих швидкостях течії і відповідно великих напругах зсуву структура повністю руйнується. Її відновлення в порівнянні з процесом руйнування йде так повільно, що вже не має впливу на характер течії.

Залежність в’язкості структурованих систем від швидкості деформації широко використовується на практиці. Наприклад, для перекачки соняшникової олії треба вибрати таку швидкість, щоб олія мала мінімальну в’язкість (що відповідає практично зруйнованій структурі) і при цьому будуть найменші витрати енергії при транспортуванні. Але під час перевезення олії в цистернах її в’язкість повинна бути максимальною.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. VІI. Утворіть вищий та найвищий ступені порівняння від прислівників із вправи VI.
3. Асимптотичний підхід до порівняння оцінок
4. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
5. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
6. Векторне канонічне параметричне рівняння прямої в просторі.
7. Вивід основного рівняння фільтрації
8. Визначення типу порівняння даних
9. Використання рівняння номінальних витрат за моделлю COCOMO II
10. ВПРАВА 2. Утворіть де можливо, форми ступенів порівняння від поданих прикметників.
11. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
12. Гіпербола та її рівняння

Переглядів: 1089