
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Теорема Остроградського-Ґаусса
Нехай навколо точкового заряду q описана сферична поверхня радіусом r, в центрі якої знаходиться цей заряд (рис. 5).
Проекція вектора напруженості En„ на напрям нормалі буде:
 ,
,
тоді потік вектора напруженості через замкнену сферичну поверхню буде:
 .
.
Отже 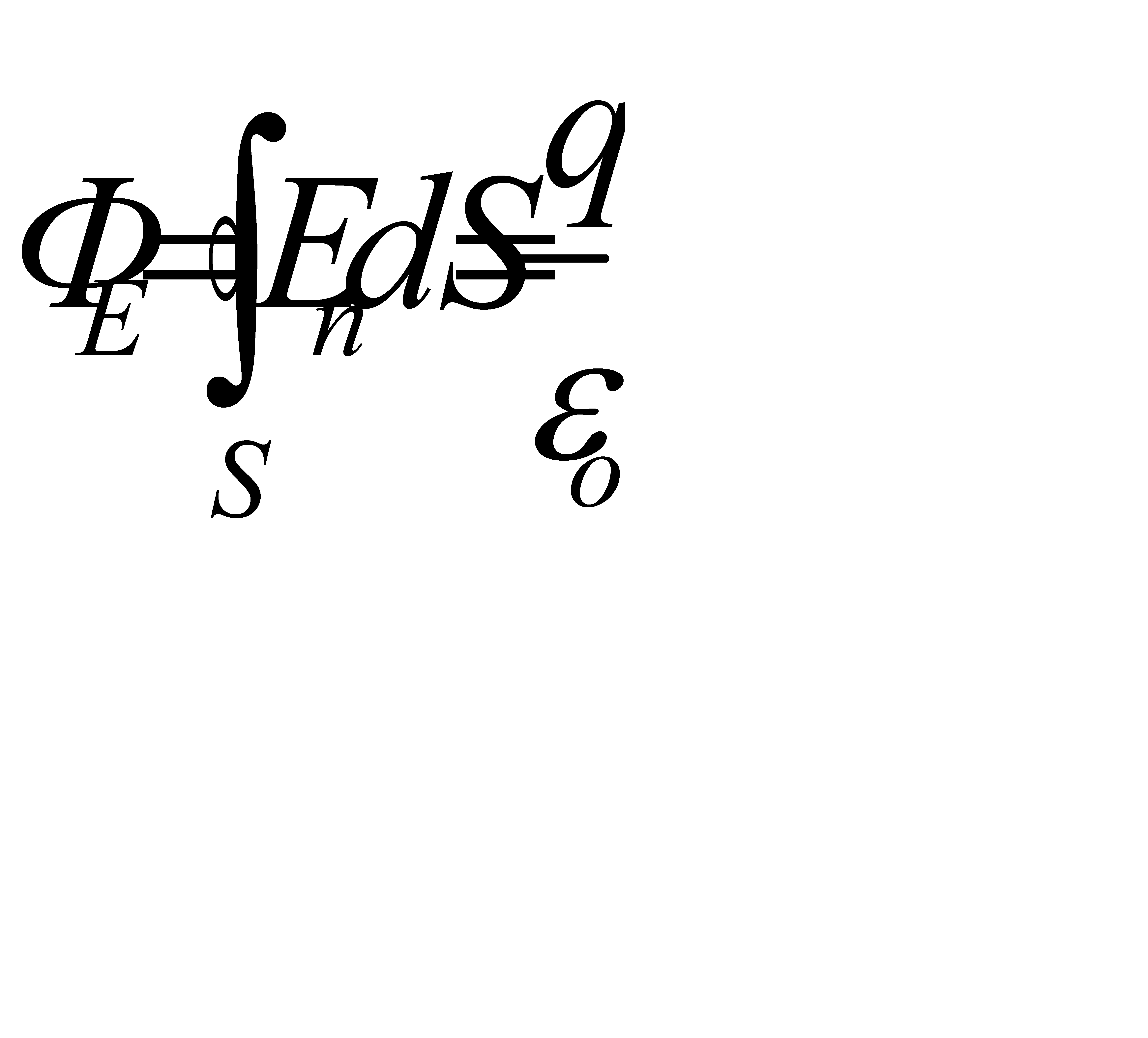 .
.
Це рівняння називається теоремою Остроградського - Ґаусса. Воно справедливе не лише для сферичних поверхонь, але і для будь-яких замкнених поверхонь, і для будь-якої кількості зарядів, що нею охоплюються. В загальному вигляді ця теорема записується так:
 .
.
Потік вектора напруженості електричного поля через замкнену поверхню дорівнює алгебраїчній сумі електричних зарядів, які охоплює ця поверхня, поділеній на електричну сталу.
Потік вектора напруженості електричного поля через довільну замкнену поверхню, що не охоплює заряду, дорівнює нулю.

| Рис. 6 |

| Рис. 7 |
 напрямлений назовні, Еn та ФE додатні, а коли
напрямлений назовні, Еn та ФE додатні, а коли  входить всередину поверхні, Еn та ФЕ – від’ємні (рис. 6).
входить всередину поверхні, Еn та ФЕ – від’ємні (рис. 6).
Для замкнених поверхонь
 .
.
Нехай навколо точкового заряду q описана сферична поверхня радіусом r, в центрі якої знаходиться цей заряд (рис.7).
18. Застосування теореми Остроградського-Ґаусса до розрахунку напруженості електростатичних полів
| s |
| DS |
| E¢ |
| E¢¢ |
| n |
Нехай поле створюється безкінечною, рівномірно зарядженою площиною із поверхневою густиною зарядів s (рис.1).
Рис. 8
| +s |
| –s |
| Рис. 9 |
Виберемо замкнуту поверхню у формі циліндра із площею DS.
В силу симетрії Е¢=Е¢¢=Е. Застосуємо теорему Остроградського-Гауса.
Потік  через бічну поверхню циліндра відсутній, так як Еп=0. Залишається тільки потік вектора
через бічну поверхню циліндра відсутній, так як Еп=0. Залишається тільки потік вектора  через поверхні основи, який дорівнює:
через поверхні основи, який дорівнює:
 .
.
Всередині замкнутої поверхні знаходиться електричний заряд, який дорівнює:
 .
.
Отже,  , звідки
, звідки
 .
.
| +s |
| –s |
| Рис. 10 |
| Е+ |
| Е+ |
| Е+ |
| Е– |
| Е– |
| Е– |
Поле, яке створюється двома безкінечними зарядженими площинами:
Як слідує із рис. 3 електричне поле має напруженість тільки між пластинами, яка визначається:
 .
.
Лекція №8
19. Потенціал електростатичного поля
Електростатичне поле точкового заряду являється потенціальним, а електростатичні сили - консервативними . Доведемо це.
Розглянемо рух пробного заряду q0 в полі, створеного зарядом q (рис.1 )
| q |
| qo |

|


|


|
| dl |
| dr |

|

Рис.1
При переміщені заряду q0 на  поле виконує елементарну роботу:
поле виконує елементарну роботу:

З врахуванням того, що dl cos(Fdl)=dr , а сила F визначається за законом Кулона,  , то вираз , що визначає елементарну роботу , набуває вигляду :
, то вираз , що визначає елементарну роботу , набуває вигляду :
 .
.
При кінечному переміщені заряду q0 з точки 1 в точку 2 повна робота, яка виконується полем , дорівнює:
 .
.
Як слідує із останього виразу, робота по переміщеню заряду q0 не залежить від траєкторії руху! Це означає, що сили, які діють на заряд – консервативні, а електростатичне поле – потенціальне. Для потенціального поля  .
.
Тіло, яке знаходиться у потенціальному полі сил, володіє потенціальною енергією, за рахунок якої силами поля виконується робота. Тому роботу сил електростатичного поля можна уявити як різницю потенціальних енергій, якими володіє точковий заряд q0 в початковій та кінцевій точках поля, створеного зарядом q.
 .
.
Потенціальну енергію заряду q0 в полі заряду q можна виразити слідуючим чином :
 .
.
Для одноіменних зарядів значення потенціальної енергії додатнє (Wп>0) для різноіменних – від’ємне (Wп<0).
Із одержаних формул витікає, що відношення Wп/q0 - не залежить від величини заряда q0 і являється енергетичною характеристикою електростатичного поля. Ця величина називається потенціалом:
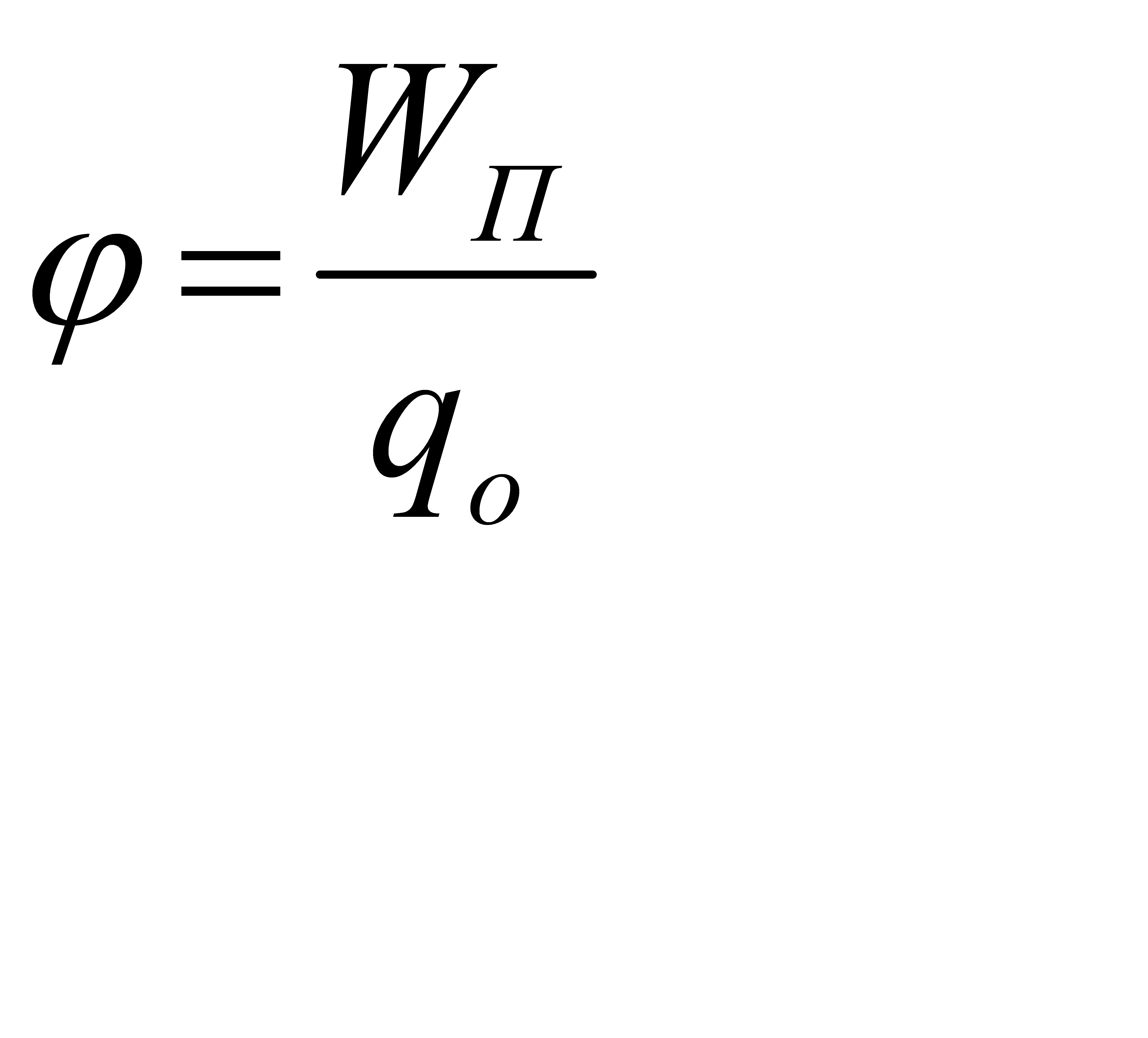 .
.
Читайте також:
- Базовою для інтегрального числення є така теорема: ТЕОРЕМА 2. Якщо функція неперервна, то для неї існує
- В. Друга теорема про розклад.
- Визначений інтеграл, як границя інтегральної суми. Теорема існування. Геометричний зміст визначеного інтеграла.
- Друга теорема Вейєрштрасса
- Екстремум ф-ї. Необхідна умова існування екстремуму. (Теорема Ферма).
- Зовнішні ефекти. Теорема Коуза
- Інтегральна теорема Лапласа
- Лекція 2 Операції над подіями. Теорема додавання ймовірностей. Умовні ймовірності. Теорема множення ймовірностей. Ймовірність здійснення принаймні однієї з незалежних подій
- Локальна теорема Лапласа
- Локальная теорема Лапласа.
- Магнітний потік. Теорема Гауса для магнітного поля
- Момент інерції. Теорема Гюйгенса-Штейнера
| <== попередня сторінка | | | наступна сторінка ==> |
| Потік вектора напруженості. | | | Потенціал j в будь-якій точці електростатичного поля це фізична величина, яка визначається потенціальною енергією одиничного додатнього заряду, поміщеного в цю точку поля. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |