• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Система параметрів і характеристик рівняння регресії

Після теоретичних досліджень поставленої проблеми, вибору виду рівняння, збору і обробки інформації настає важлива стадія в процесі використання методів кореляції і регресії - визначення параметрів рівняння (а₀,а_і) і статистичних характеристик, за допомогою яких оцінюється якість рівняння.

Параметри будь-якого рівняння регресії визначаються методом найменших квадратів.

На основі методу найменших квадратів формується система нормальних рівнянь, склад яких залежить від виду рівняння регресії.

Стосовно парного лінійного рівняння і квадратичного рівняння система нормальних рівнянь має такий вигляд:

У = а₀ + а₁ х

∑у = n а₀ + а₁ ∑х

∑ху = а₀ ∑х + а₁ ∑х²

У = а₀ + а₁ х + а₂ х²

∑у = n а₀ + а₁ ∑х + а₂ ∑х²

∑ху = а₀ ∑х + а₁ ∑х² + а₂ ∑х³

∑х²у = а₀ ∑х² + а₁ ∑х³ + а₂ ∑х⁴

Найбільш важливою характеристикою рівняння, що відображає і його якість і цінність, є тіснота зв'язку між фактором (факторами) і результативною ознакою.

Для оцінки тісноти зв'язку використовуються:

- в парних рівняннях – парний лінійний коефіцієнт кореляції (r);

- в парних нелінійних рівняннях – парне кореляційне відношення ();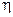

- в багатофакторних множинних лінійних рівняннях – множинний лінійний коефіцієнт кореляції (R);

- в множинних нелінійних рівняннях – множинне кореляційне відношення ().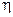

Парний лінійний коефіцієнт кореляції обчислюється за формулою:

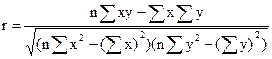
Лінійний множинний коефіцієнт кореляції, кореляційне відношення (парне і множинне) розраховуються за однаковою формулою:

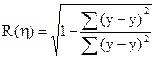
Для оцінки рівня зв'язку між досліджуваними ознаками використовуються певні межі:

Таблиця – Оцінка рівня зв'язку

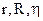
Величина	До 0,5	0,5-0,6	0,6-0,7	0,7-0,8	0,8-0,9	Більше 0,9
Сила зв'язку	Дуже низький	низький	помітний	середній	сильний	Дуже сильний

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
3. I. Загальна характеристика політичної та правової думки античної Греції.
4. II. Бреттон-Вудська система (створена в 1944 р.)
5. II. ВИРОБНИЧА ХАРАКТЕРИСТИКА ПРОФЕСІЇ
6. II. Морфофункціональна характеристика відділів головного мозку
7. IV. Система зв’язків всередині центральної нервової системи
8. IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
9. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
10. V. Поняття та ознаки (характеристики) злочинності
11. V. Систематизація і узагальнення нових знань, умінь і навичок
12. VI. Система навчаючих завдань для перевірки кінцевого рівня завдань.

Переглядів: 744