Найпростіший потік подій

Розглянемо події, які наступають у випадкові моменти часу.

Потоком подій називають послідовність подій, які наступають у випадкові моменти часу. Прикладами потоків служать: надходження викликів на АТС, на пункт невідкладної медичної допомоги, прибуття літаків до аеропорту, клієнтів на підприємство побутового обслуговування, послідовність відмов елементів і багато інших.

Серед властивостей, якими можуть бути властиві потокам, виділимо властивості стаціонарності, відсутності післядії і ординарності.

Властивість стаціонарності характеризується тим, що ймовірність появи k подій на будь-якому проміжку часу залежить тільки від числа k і від тривалості t проміжку і не залежить від початку його відліку; при цьому різні проміжки часу передбачаються непересічними. Наприклад, ймовірності появи k подій на проміжках часу (1; 7) (10; 16) (Т; Т+ 6) однакової тривалості t=6 од. часу рівні між собою.

Отже, якщо потік володіє властивістю стаціонарності, то ймовірність появи k подій за проміжок часу тривалості t є функція, залежна тільки від k і t.

Властивість відсутності післядії характеризується тим, що ймовірність появи k подій на будь-якому проміжку часу не залежить від того, з’являлися або не з’являлися події в моменти часу, що передували початку даного проміжку. Іншими словами, умовна ймовірність появи k подій на будь-якому проміжку часу, обчислена при будь-яких припущеннях про те, що відбувалося до початку даного проміжку (скільки подій з’явилося, в якій послідовності), дорівнює безумовній ймовірності. Таким чином, передісторія потоку не позначається на ймовірності появи подій в найближчому майбутньому.

Отже, якщо потік володіє властивістю відсутності післядії, то має місце взаємна незалежність появ того або іншого числа подій в непересічні проміжки часу.

Властивість ординарності характеризується тим, що поява двох і більше подій за малий проміжок часу практично неможлива. Іншими словами, ймовірність появи більше однієї події нікчемно мала в порівнянні з ймовірністю появи тільки однієї події.

Отже, якщо потік володіє властивістю ординарності, то за нескінченно малий проміжок часу може з’явитися не більше однієї події.

Найпростішим (пуассонівским) називають потік подій, який володіє властивостями стаціонарності, відсутності післядії і ординарності.

Зауваження. Часто на практиці важко встановити, чи володіє потік перерахованими вище властивостями. Тому були знайдені і інші умови, при дотриманні яких потік можна вважати найпростішим або близьким до найпростішого. Зокрема, встановлено, що якщо потік представляє собою суму дуже великого числа незалежних стаціонарних потоків, вплив кожного з яких на суму (сумарний потік) нікчемно малий, то сумарний потік (за умови його ординарності) близький до найпростішого.

Інтенсивністю потоку 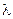називають середнє число подій, які з’являються в одиницю часу.

Можна довести, що якщо постійна інтенсивність потоку відома, то ймовірність появи k подій найпростішого потоку за час тривалістю t визначається формулою Пуассона

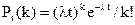Ця формула відображає всі властивості найпростішого потоку.

Дійсно, з формули видно, що ймовірність появи k подій за час t, при заданій інтенсивності є функцією k і t, що характеризує властивість стаціонарності.

Формула не використовує інформації про появу подій до початку даного проміжку, що характеризує властивість відсутності післядії.

Переконаємося, що формула відображає властивість ординарності. Поклавши k=0 і k=1, знайдемо відповідно ймовірності не появи подій і появи однієї події:

, .

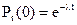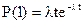Отже, ймовірність появи більше однієї події

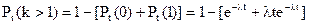Користуючись розкладанням

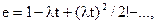
після елементарних перетворень отримаємо

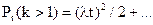Порівнюючи P_t(1) і P_t(k>l), робимо висновок, що при малих значеннях t ймовірність появи більше одної події нікчемно мала в порівнянні з ймовірністю появи однієї події, що характеризує властивість ординарності.

Отже, формулу Пуассона можна вважати математичною моделлю найпростішого потоку подій.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Розподіл Пуассона	\|	Геометричний розподіл

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.