
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Виникнення (походження) держави. 1 страница
7.
План
План
План
План
План
План
План
План
Р.
З практичними завданнями
Лист контролю.
Модуль №10.
1. Елементи комбінаторики.
2. Предмет теорії імовірності.
3. Види випадкових подій.
4. Операції над подіями.
5. Частота і імовірність події.
6. Теореми додавання імовірності.
7. Теореми множення імовірності.
8. Формула повної імовірності.
9. Незалежні випробування. Формула Бернуллі.
10. Дискретні випадкові величини. Закон розподілу.
11. Числові характеристики випадкових величин.
12. Закон великих чисел.
13. Предмет математичної статистики. Вибірки. Статистичний розподіл.
14. Числові характеристики вибірки.
15. Сумісний розподіл випадкових величин. Рівняння лінійної регресії.
Література:
1. О.М. Афанасьєва «Математика». 2001р.
2. О.М. Афанасьєва «Дидактичні матеріали з математики».2001р.
3. М.І. Шкіль «Алгебра і початки аналізу». 10 – 11кл. 1995р.
4. И.И. Валуйэ «Математика для техникумов». 1990р.
5. Н.В. Богомолов «Практические занятия по математике». 1990р.
з дисципліни
“Математика”
для студентів І курсу усіх форм навчання усіх спеціальностей
Опорні конспекти розроблені викладачами дисципліни „Математика”
Вороніною Н.К., Голубковою І.М
Розглянуто і затверджено цикловою комісією природничо – математичних дисциплін.
Протокол № від “ ” вересня 20 р.
Рецензенти:
ЗМІСТ
1. Розділ 1 ФУНКЦІЇ, ЇХ ВЛАСТИВОСТІ ТА ГРАФІКИ............................................................................................... ...5
1.1 Функції та їх властивостії ...................................................................................................................5
1.2 Графіки елементарних функцій та їх перетворення............................................................................................6
1.3 Приклади для розв’язування...........................................................................................7
2. Розділ 2 ГРАНИЦІ ФУНКЦІЇ В ТОЧЦІ ТА
НА НЕСКІНЧЕННОСТІ ТА ЇХ ВИКОРИСТАННЯ
ДЛЯ ДОСЛІДЖЕННЯ ФУНКЦІЙ................................................................................................10
2.1 Границя функції в точці................................................................10
2.2. Границя функції на нескінченності..............................................12
2.3 Дослідження функції на неперервність.......................................13
2.4. Приклади для розв’язування........................................................13
3. Розділ 3. ТРИГОНОМЕТРІЯ.............................................................17
3.1 Визначення та графіки тригонометричних функцій....................17
3.2 Основні формули тригонометрії...................................................19
3.3 Найпростіші тригонометричні рівняння........................................21
3.4. Приклади для розв’язування........................................................23
4. Розділ 4. СТЕПЕНІ ТА ЛОГАРИФМИ.........................................................................................26
4.1 Степені та корені...........................................................................26
4.2 Логарифми.....................................................................................27
4.4. Приклади для розв’язування........................................................28
5. Розділ 5. ПОХІДНА ФУНКЦІЇ ТА ЇЇ
ВИКОРИСТАННЯ...................................................................................40
5.1 Похідна функції, її фізичний та геометричний зміст............40
5.2 Правила диференціювання та таблиця похідних................42
5.3 Використання похідної для дослідження функцій................44
5.4 Приклади для розв’язування.................................................44
6. Розділ 6. ІНТЕГРАЛ ТА ЙОГО ВИКОРИСТАННЯ..........................50
6.1 Невизначений інтеграл та його властивості................................50
6.2 Таблиця невизначених інтегралів...............................................51.
6.3 Визначений інтеграл......................................................................52
6.4. Використання визначеного інтегралу
для обчислення площ плоских фігур..........................................53
6..4 Приклади для розв’язування........................................................54
7. Розділ 7. ВЕКТОРИ ТА КООРДИНАТИ...........................................60
7.1. Визначення вектора та дії з векторами.......................................60
7.2....Рівняння прямої на площині.........................................................62
7.3 Розв’язання систем лінійних рівнянь
.........за формулами Крамера................................................................63
7.4. Приклади для розв’язування.................................................64
8. Розділ 8. СТЕРЕОМЕТРІЯ.............................................................67
8.1. Аксіоми стереометрії....................................................................67
8.2 Теореми стереометрії..................................................................68
8.3 Площі плоских геометричних фігур............................................69
8.4. Площі поверхонь та об’єми деяких тіл.......................................70
8.5. Приклади для розв’язування......................................................73
Рівні засвоєння навчального матеріалу:
- перший рівень – початковий – відповідь студента при відтворенні навчального матеріалу – елементарна, фрагментарна, зумовлюється початковими уявленнями про предмет вивчення;
- другий рівень – середній – студент відтворює основний навчальний матеріал, здатний розв’язувати завдання за зразком, володіє елементарними вміннями навчальної діяльності (*);
- третій рівень – достатній– студент знає істотні ознаки понять, явищ, закономірностей зв’язків між ними, а також самостійно застосовує знання в стандартних ситуаціях, володіє розумовими операціями (аналізом, абстрагуванням, узагальненням тощо), уміє робити висновки, виправляти допущені помилки; відповідь повна, правильна, логічна, обгрунтована, хоча їй бракує власних суджень (**);
- четвертий рівень – високий – знання студента є глибокими, міцними, узагальненими, системними; студент уміє застосовувати знання творчо, його навчальна діяльність має дослідницький характер, позначена вмінням самостійно оцінювати різноманітні життєві ситуації, явища, факти, виявляє і відстоює особисту позицію (***).
Розділ 1. ФУНКЦІЇ, ЇХ ВЛАСТИВОСТІ ТА ГРАФІКИ
1. Визначення функції та способи задання.
2. Властивості функції.
3. Графіки елементарних функцій та їх властивості.
4. Перетворення графіків елементарних функцій
5. Приклади для розв’язування.
1. Функцією називається відповідність між двома множинами, при якій кожному елементу однієї множини ( області визначення ) відповідає єдиний елемент іншої множини ( області значень ).
Область визначення функції має обмеження у таких випадках:
· 
· 
· 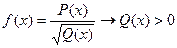
2. Функція зростає, якщо більшому значенню аргумента відповідає більше значення функції і спадає в іншому випадку:
f(x) ↑↔ x2>x1→ f(x2)>f(x1);
f(x) ↓↔ x2>x1→ f(x2)<f(x1);
Функція парна, якщо при зміні значення аргументу на протилежне значення функції не змінюється: f (-x) =f(x).
Функція непарна, якщо при зміні значення аргументу на протилежне значення функції змінюється на протилежне: f (-x) = - f(x).
Функція, що не являється непарною та парною називається функцією загального вигляду.
3. Елементарні функції та їх графіки
| № п/п | Назва функції. | Формула. | Графік. | |||
| 1. | Лінійна функція |

| Пряма лінія.
 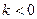
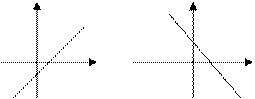
| |||
| 2. | Пряма пропорційність. |
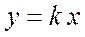
| Пряма лінія, що проходить через початок координат.
 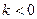
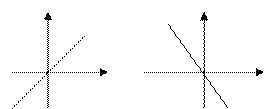
| |||
| 3. | Обернена пропорційність. |

| Гіпербола.
 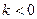
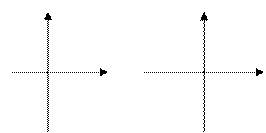
| |||
| 4. |
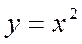
| 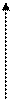 Парабола. Парабола.

| ||||
| 5. |
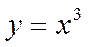
|  Кубічна парабола. Кубічна парабола. 
| ||||
| 6. |
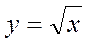
| «Лежача» вітка параболи

| ||||
| 7. |
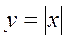
|  Кут, утворений бісектрисами 1 та 2 чверті. Кут, утворений бісектрисами 1 та 2 чверті.
|
4. Найпростіші перетворення графіків функцій.
| № п/п | Функція | Перетворення. |
| | 
| Одержується з графіка функції 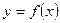 зміщенням вздовж осі Оу вгору на зміщенням вздовж осі Оу вгору на 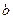 одиниць, якщо одиниць, якщо 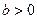 ; вниз, якщо ; вниз, якщо  . .
|
| | 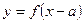
| Одержується з графіка функції 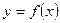 зміщенням вздовж осі Ох вправо на зміщенням вздовж осі Ох вправо на 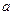 одиниць, якщо одиниць, якщо 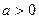 ; вліво, якщо ; вліво, якщо 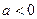 . .
|
| | 
| Одержується симетричним відображенням графіка функції 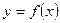 відносно осі Ох. відносно осі Ох.
|
| | 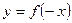
| Одержується симетричним відображенням графіка функції 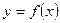 відносно осі Оу. відносно осі Оу.
|
| | 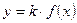 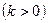
| Одержується з графіка функції 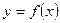 розтягненням вздовж осі Оу в розтягненням вздовж осі Оу в 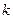 разів, якщо разів, якщо 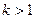 ; або стисненням до осі Ох, якщо ; або стисненням до осі Ох, якщо 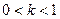 . .
|
| | 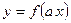 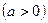
| Має той самий вигляд, що й у графіка 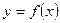 , тільки розтягнено від осі Ох, якщо , тільки розтягнено від осі Ох, якщо 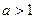 , або стиснено до осі Ох, якщо , або стиснено до осі Ох, якщо 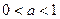 . .
|
| | 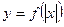
| Ділянки графіка 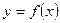 , які лежать праворуч від осі Оу – без зміни, і ця ж сама частина симетрично відображається відносно осі Оу. , які лежать праворуч від осі Оу – без зміни, і ця ж сама частина симетрично відображається відносно осі Оу.
|
| | 
| Ділянки графіка 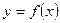 , які лежать вище від осі Ох – без зміни, а та частина, що нижче від осі Ох - симетрично відображається відносно осі Ох. , які лежать вище від осі Ох – без зміни, а та частина, що нижче від осі Ох - симетрично відображається відносно осі Ох.
|
| | 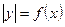
| Ділянки графіка 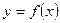 , які лежать вище від осі Ох – без зміни, і ця ж сама частина симетрично відображається відносно осі Ох. , які лежать вище від осі Ох – без зміни, і ця ж сама частина симетрично відображається відносно осі Ох.
|
5. Приклади для розв’язування.
1.Дослідити функції на парність.
1) 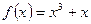
2) 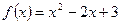
3) 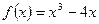
4) 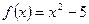
5) *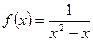
6) *
7) **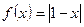
8) **
9) **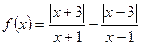
10) **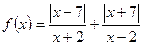
11) ***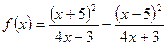
12) ***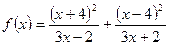
2. Знайти область визначення функції.
1) 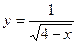
2) 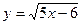
3) 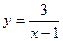
4) *
5) *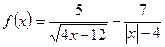
6) *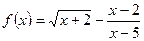
7) *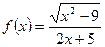
8) **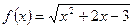
9) **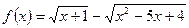
10) **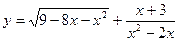
11) **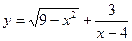
12) **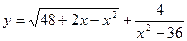
13) ***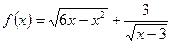
14) ***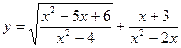
15) ***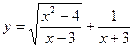
16) ***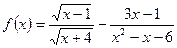
17) ***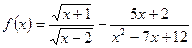
3. Побудувати графік функції та указати область значень:
1. 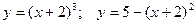
2. 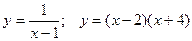
3. 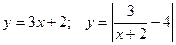
4. 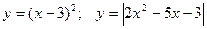
5. 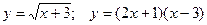
6. 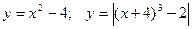
Розділ 2. ГРАНИЦІ ФУНКЦІЇ В ТОЧЦІ ТА НА НЕСКІНЧЕННОСТІ ТА ЇХ ВИКОРИСТАННЯ ДЛЯ ДОСЛІДЖЕННЯ ФУНКЦІЙ
1. Границя функції в точці.
2. Теореми про границі.
3. Правила обчислення границь.
4. Границя на нескінченності.
5. Дослідження функції на неперервність
1. Границя функції в точці
Нехай функція 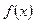 визначена в деякому околі Х точки
визначена в деякому околі Х точки 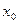 (крім можливо самої точки
(крім можливо самої точки 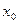 ).
).
Число А називається границею функції 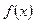 при
при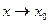 , якщо для довільного
, якщо для довільного 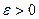 існує число
існує число 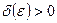 таке, що для всіх
таке, що для всіх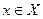 , які задовольняють нерівність:
, які задовольняють нерівність: 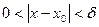 , виконується нерівність
, виконується нерівність  .
.
 Пишуть:
Пишуть: 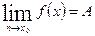
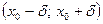 -
- 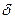 - окіл точки
- окіл точки 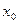
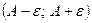 -
- 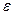 - окіл точки А
- окіл точки А
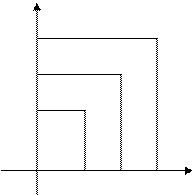
Геометрично це означає: що будь – якій точці з 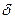 - околу відповідає деяка точка з
- околу відповідає деяка точка з 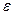 - околу.
- околу.
2. Теореми про границі.
Якщо кожна з функцій 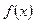 і
і 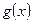 має скінченну границю при
має скінченну границю при 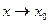
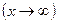 , то справедливі формули:
, то справедливі формули:
1) 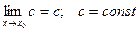
2) 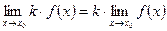
3) 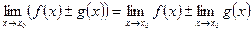
4) 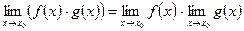
5) 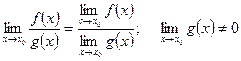
3. Правила обчислення границь.
1. Якщо функція дробово – раціональна, то для знаходження границі чисельник і знаменник розкладають на множники, які потім скорочують, причому скоротитись повинен той множник, який обертається в нуль.

2. Якщо чисельник функції – стала величина, а границя знаменника дорівнює нулю, то границя такої функції є нескінченність.
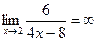
3. Якщо функція містить знаки радикалів, то чисельник і знаменник помножають на вираз, спряжений до чисельника (знаменника), а потім застосовують формулу різниці квадратів. Вирази 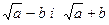 та
та 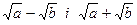 називаються спряженими.
називаються спряженими.
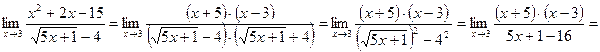
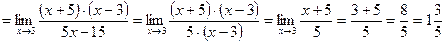
4. Якщо функція містить корінь третього степеня, то чисельник і знаменник помножають на неповний квадрат суми або різниці, а потім застосовують формулу суми або різниці кубів.
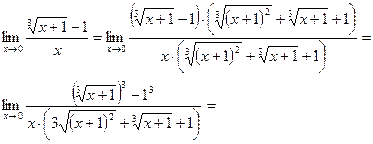
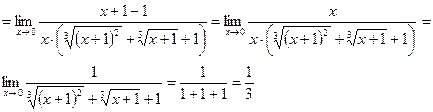
4. Границя функції на нескінченності.
Границею на нескінченності називається число, до якого прямує значення функції, якщо аргумент нескінченно зростає.
1. Границя функції, яка представляє собою многочлен, при 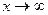 є нескінченність.
є нескінченність.

2. Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника і знаменника однакові дорівнює відношенню коефіцієнтів при старших членах.
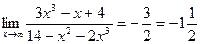
3. Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника менша за степінь знаменника, дорівнює нулю.
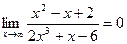
4. Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника більша за степінь знаменника, дорівнює нескінченності.
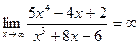
5.Дослідження функції на неперервність.
Функція 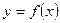 називається неперервною в точці
називається неперервною в точці 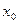 , якщо вона в цій точці визначена і нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції:
, якщо вона в цій точці визначена і нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції: 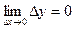 .
.
Функція 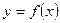 називається неперервною в точці
називається неперервною в точці 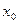 ,якщо виконуються слідуючи умови:
,якщо виконуються слідуючи умови:
1) функція визначена в точці 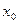 ;
;
2) існує границя функції в точці 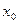 ;
;
3) значення функції в точці 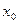 співпадає із значенням границі в точці
співпадає із значенням границі в точці 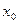 .
.
Число А називається границею функції 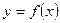 справа при
справа при 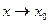 ,
, 
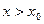 , якщо функція визначена у правому
, якщо функція визначена у правому 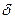 - околі точки
- околі точки 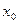 , і для будь – якого
, і для будь – якого 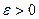 знайдеться таке
знайдеться таке 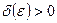 , що для всіх
, що для всіх  , взятих з інтервалу
, взятих з інтервалу 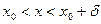 виконується нерівність
виконується нерівність  .
.
Позначають 
Число А називається границею функції 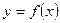 зліва при
зліва при 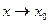 ,
, 
 , якщо функція визначена у лівому
, якщо функція визначена у лівому 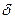 - околі точки
- околі точки 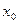 , і для будь – якого
, і для будь – якого 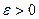 знайдеться таке
знайдеться таке 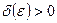 , що для всіх
, що для всіх  , взятих з інтервалу
, взятих з інтервалу 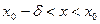 виконується нерівність
виконується нерівність  .
.
Читайте також:
- I. ОБРАЗОВАНИЕ СОЕДИНЕННЫХ ШТАТОВ 14 страница
- XVII ст.). Виникнення козацтва.
- А. В. Дудник 1 страница
- А. В. Дудник 10 страница
- А. В. Дудник 11 страница
- А. В. Дудник 12 страница
- А. В. Дудник 2 страница
- А. В. Дудник 3 страница
- А. В. Дудник 4 страница
- А. В. Дудник 5 страница
- А. В. Дудник 6 страница
- А. В. Дудник 7 страница
| <== попередня сторінка | | | наступна сторінка ==> |
| Статистики. | | | Виникнення (походження) держави. 2 страница |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |

