РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
План-конспект урока 5 страница
4. Визначений інтеграл.
5. Формула Ньютона – Лейбніца.
6. Використання визначених інтегралів для обчислення площ плоских фігур.
7. Приклади для розв’язування задач.
1. Первісна та невизначений інтеграл.
В багатьох практичних задачах необхідно по заданій похідній відновити первісну функцію.
Означення. Функція F(x) називається первісною для функції f(x) на проміжку (а; b), , якщо на цьому проміжку 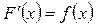 .
.
Операція знаходження первісних для функції f(x) називається інтегруванням f(x).
Означення:Невизначеним інтегралом для неперервної функції 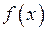 називають множину всіх первісних функцій
називають множину всіх первісних функцій  і позначають
і позначають
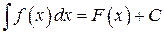
де:
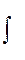 — знак невизначеного інтеграла;
— знак невизначеного інтеграла;
f(x) — підінтегральна функція;
f(x) dx — підінтегральний вираз;
dx — диференціал змінної інтегрування.
2. Основні властивості невизначеного інтеграла.
1)  ;
;
2)  ;
;
3)  ;
;
4) 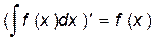 .
.
3. Таблиця невизначених інтегралів.
1. 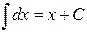 ;
;
2.  ;
;
3.  ;
;
4. 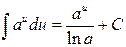 ;
;
5. 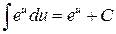 ;
;
6.  ;
;
7. 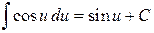 ;
;
8. 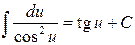 ;
;
9. 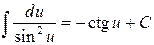 ;
;
10. 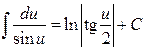 ;
;
11. 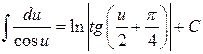 ;
;
12. 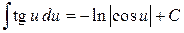 ;
;
13. 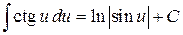 ;
;
14. 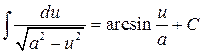 ;
;
15.  ;
;
16. 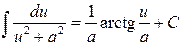 ;
;
17.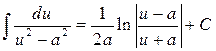
4. Визначений інтеграл
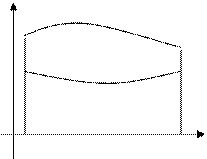
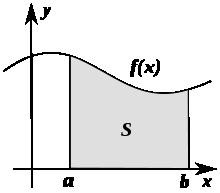 Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний смисл цього визначеного інтеграла — це площа криволінійної фігури, обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.
Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний смисл цього визначеного інтеграла — це площа криволінійної фігури, обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.
6.Формула Ньютона – лейбніца.
Якщо у функції f(x) існує первісна F(x), то
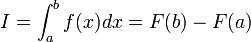
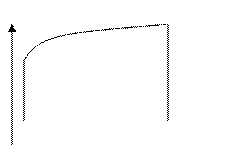
7. Використання інтегралів для обчислення площі плоских фігур
| № п/п | Назва поняття. | Геометричне зображення | Формула для обчислення. | |||
| 1. |  Площа криволінійної трапеції, якщо Площа криволінійної трапеції, якщо 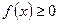 на відрізку на відрізку 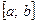
| 
| 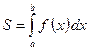
| |||
| 2. | Площа криволінійної трапеції, якщо 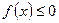 на відрізку на відрізку 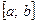
| 
| 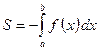
| |||
| 3. | Якщо фігура обмежена графіками неперервних на відрізку 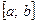 функціями функціями 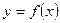 і і 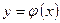 , при чому , при чому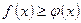
|
| 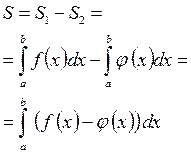
| |||
| 4. | 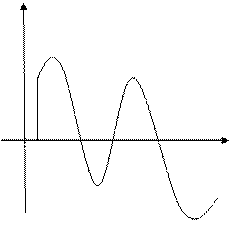 Якщо функціями Якщо функціями 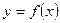 кілька разів змінює знак на відрізку кілька разів змінює знак на відрізку 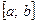 , то інтеграл для обчислення площі на всьому відрізку , то інтеграл для обчислення площі на всьому відрізку 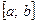 розбиваємо на частини. Інтеграл буде додатній на тих частинах, де розбиваємо на частини. Інтеграл буде додатній на тих частинах, де 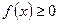 і від’ємний там де і від’ємний там де 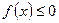 . .
|
| 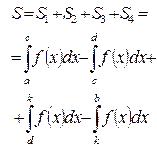
|
9. Приклади для розв’язування.
1. Знайти невизначені інтеграли.
1) 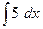
2) 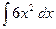
3) 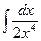
4) 
5) 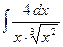
6) 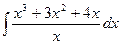
7) 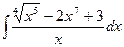
8) 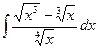
9) 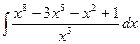
10) 
11) 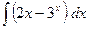
12) 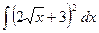

13) 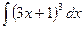
14) 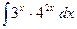
15) 
16) 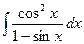
17) 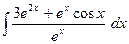
18) 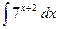
19) 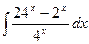
20) 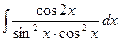
21) 
22) 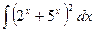
23) 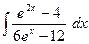
24) 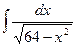
25) 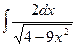
26) 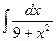
27) 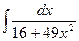
28) 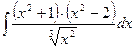
29) 
30) 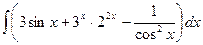
31) 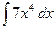
32) 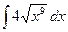
33) 
34) 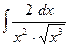
35) 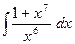
36) 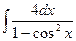
37) 
38) 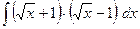
39) 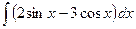
40) 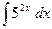
41) 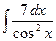
42) 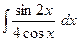
43) 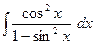
44) 
45) 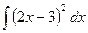

2.** Знайти невизначені інтеграли.
1) 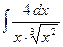
2) 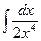
3) 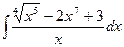
4) 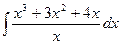
5) 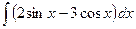
6) 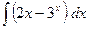
7) 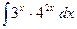
8) 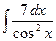
9) 
10) 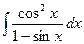
11) 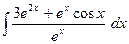
12) 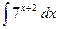
13) 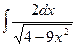
14) 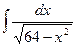
15) 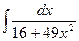
16) 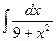
17) 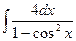
18) 
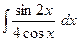
3.* Знайти невизначений інтеграл методом заміни змінної.
1.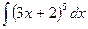
2.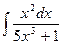
3.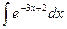
4.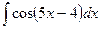
5.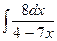
6.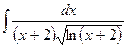
7.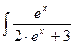
8.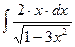
9.
10.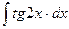
11.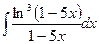
12.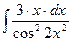
13.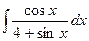
14.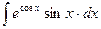
15.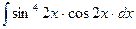
16.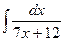
17.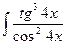
18.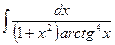
19.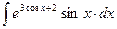
20.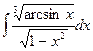
21.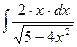
22.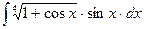
23.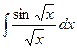
24.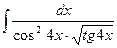
25.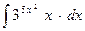
4. **Знайти невизначений інтеграл методом заміни змінної.
1)
2)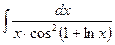
3)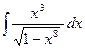
4)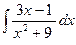
5)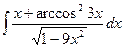
6)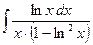
7)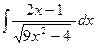
8)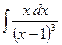
9)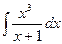
10)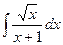
11)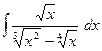
12)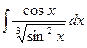
13)
14)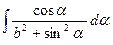
15)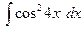
16)
17)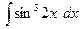
18)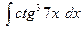
19)
20)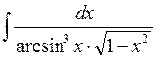
21)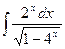
22)
23)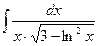
24)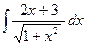
25)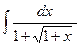
26)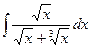
27)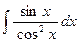
28)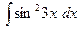
29)
30)
5. ***Обчислення невизначеного інтеграла
методом заміни змінної
1.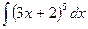
2.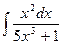
3.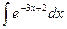
4.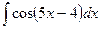
5.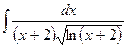
6.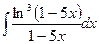
7.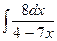
8.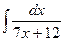
9.
10.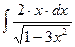
11.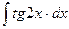
12.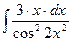
13.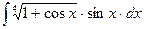
14.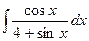
15.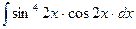
16.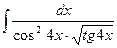
17.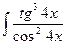
18.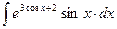
19.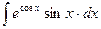
20.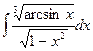
21.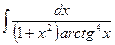
6. Обчислити визначений інтеграл.
1) 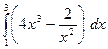
2) 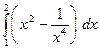
3) 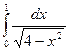
4) 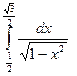
5) 
6) 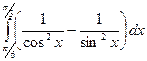
7) 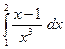
8) 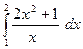
9) 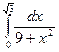
10) 
11) 
12) 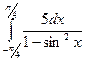
13) 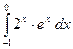
14) 
15) 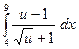
16) 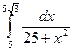
17) 
18) 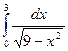
19) 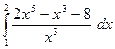
20) 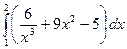
7. Обчислити площі плоских фігур, обмежених лініями:
1. х – у + 2 = 0; у = 0; х = - 1; х = 2,
2. 2х – 3у + 6 = 0; у = 0; х = 3,
3. х – у + 3 = 0; х + у – 1 = 0; у = 0;
4. х – 2у + 4 = 0, х + 2у – 8 = 0, у = 0; х = - 1; х = 6.
5. у = х2 , у = 0, х = 0, х = 3.
6. у = 3 х2 ; у = 0; х = - 3; х = 2.
7. у = х2 + 1; у = 0; х = - 1; х = 2.
8. у = 0,5х2 + 2; у = 0; х = 1; х = 3.
9. у = - (1/3)х2 + 3; у = 0; х = 0; х = 3.
10. у2 = х; у ≥ 0; х = 0; х = 3.
11. у = - х2 – 2х + 8; у = 0.
12. у = - (2/9)х2 + (4/3)х; у = 0.
13. у = - х2 + 6х -5; у = 0;х = 2; х = 3.
14. у = 1/х; у = 0; х = 1; х = 3.
15. у = 2/х; у = 0; х = 2; х = 4.
16. у = соs x, y = 0, x = 0, x = π/2.
17. y = tg x, y = 0, x = 0, x = π/3.
18. y = tg x, y = 0, x = π/6, x = π/3.
19. y = - 3x, y = 0, x = 2.
20. y = 2x, y = 0, x = - 3.
21. x – 2y – 6 = 0, y = 0.
22. x – 2y – 5 = 0, y = - 2x, y = 0.
23. y = - 3x2 , y = 0, x = 1, x = 2.
24. y = - x2 – 1, y = 0, x = - 2, x = 1.
25. y = x2 – 4, y = 0.
26. y = x3 , y = 0, x = - 2, x = 2.
27. y = 4 x3 , y = 0, x = - 1, x = 2.
28. y2 = 4x, x = 1, x = 9.
29. y2 = 9x, x = 4,
30. y = sin x, y = 0, x = - π/2, x = π.
31. y = sin x, y = 0, x = 0, x = 2π.
31. y = x2 , y = - 3x.
32. y = x2 , y = 2x + 8.
33. y = x2 , y = x + 2.
34. y = x2 + 2 , y = 6.
35. y = 0,5x2 – 4x + 10, y = x + 2.
36. y = x2 – 2x + 3, y =3 x - 1.
37. y =(1/3)x2 – 2x + 4, y = - x + 10.
38. y = 0,5x2 + 2x + 4, y = x + 8.
39. y = 2x2 + 1, y = x2 + 10.
40. y = - 1,5x2 + 9x – 7,5, y = - x2 +6x - 5.
41. y = x2 , y = 2 – x2 .
41. y = x2 – 6x + 9, 3x – y – 9 = 0.
42. y = x2 , x = y2 .
Розділ 7. ВЕКТОРИ ТА КООРДИНАТИ
1. Вектори та дії з ними.
2. Лінійні операції над векторами.
3. Рівняння прямої на площині».
4. Розв’язання систем лінійних рівнянь за формулами Крамера
5. Приклади для розв’язування.
1. Вектори та дії з ними.
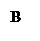
 Вектор – це напрямлений відрізок:
Вектор – це напрямлений відрізок: 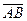 , точка А – початок вектора, точка В – кінець вектора.
, точка А – початок вектора, точка В – кінець вектора.
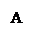 |
Нульовий вектор – це вектор, у якого початок і кінець співпадають: 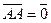 .
.
Довжина вектора (модуль, абсолютна величина) - це довжина відрізка, який зображає даний вектор: 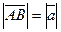 .
.
Координатами вектора називаються його проекції на осі координат.
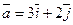 , де
, де 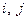 - одиничні вектори, орти.
- одиничні вектори, орти.
Якщо 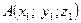 і
і  , то координати вектора
, то координати вектора 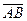 знаходяться за формулою:
знаходяться за формулою: 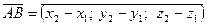
Два вектори називаються рівними, якщо вони колінеарні, однаково напрямлені та рівні по довжині
Рівні вектори мають рівні координати.
Довжина вектора: 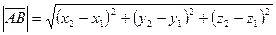 , (якщо
, (якщо 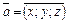 , то
, то 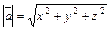 ).
).
Вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.
Якщо вектори  і
і 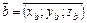 колінеарні, то їх координати пропорційні
колінеарні, то їх координати пропорційні 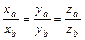 .
.
2. Лінійні операції над векторами.
| 1. | Вектор. | 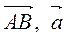
|
| 2. | Координати вектора. | 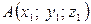 і і  , , 
|
| 3. | Довжина вектора. |  якщо
якщо 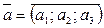 , то , то 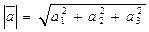 . .
|
| 4. | Додавання векторів. | 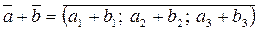
|
| 5. | Віднімання векторів. | 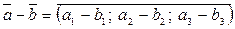
|
| 6. | Множення вектора на число. | 
|
| 7. | Скалярний добуток векторів (означення) | 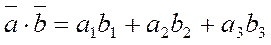
|
| 8. | Теорема про скалярний добуток векторів | 
|
| 9. | Кут між векторами. | 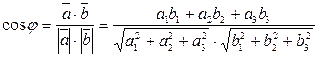
|
| 10. | Умова колінеарності векторів. | 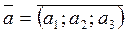 , , 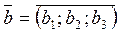 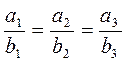 . .
|
| 11. | Умова перпендикулярності векторів. | 
|
3. Рівняння прямої на площині».
Читайте також:
- I. ОБРАЗОВАНИЕ СОЕДИНЕННЫХ ШТАТОВ 14 страница
- А. В. Дудник 1 страница
- А. В. Дудник 10 страница
- А. В. Дудник 11 страница
- А. В. Дудник 12 страница
- А. В. Дудник 2 страница
- А. В. Дудник 3 страница
- А. В. Дудник 4 страница
- А. В. Дудник 5 страница
- А. В. Дудник 6 страница
- А. В. Дудник 7 страница
- А. В. Дудник 8 страница
| <== попередня сторінка | | | наступна сторінка ==> |
| План-конспект урока 4 страница | | | План-конспект урока 6 страница |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |