• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рівняння поверхні рівня.

Якщо взяти ряд точок, в котрих гідростатичний тиск однаковий, тобто виконується вимога p = f (х, y, z) = const, і провести через ці точки поверхню, то вона буде називатися поверхнею рівного тиску. Іноді такі поверхні називаються поверхнями рівня.

Для одержання рівняння поверхні рівного тиску скористаємося основним диференціальним рівнянням гідростатики. Тому що для поверхні рівного тиску p = f (x, y, z) = const, то dp=0.

Таким чином, для поверхні рівного тиску одержимо

X∙dx +Y∙dy + Z∙dz =0 . (7)

Це рівняння встановлює зв'язок між координатами поверхні рівного тиску нерухомої рідини і діючими на рідину прискореннями масових сил. Окремим випадком якого є рівняння вільної поверхні крапельної рідини.

Розглянемо кілька конкретних випадків рівноваги рідини і встановимо вид поверхні рівного тиску (у тому числі й вільної поверхні) в кожному з цих випадків.

Приклад 1. Рідина знаходиться в рівновазі в резервуарі в поле дії тільки сили тяжіння (рис. 5а). У цьому випадку проекції результуючої одиничних масових сил будуть такими: Х = 0, Y = 0, Z =-g. Підставляючи ці значення в (7), отримаємо:

- g∙dz = 0,

або після інтегрування:

dz = const.

Це рівняння горизонтальної площини. Отже, в однорідній рідині (ρ = const), яка покоїться, будь-яка горизонтальна площина є площиною рівного тиску.

Рис. 5 Випадки рівноваги рідини

Приклад 2. Рідина знаходиться в рівновазі в резервуарі, який рухається горизонтально з деяким прискоренням а (рис. 5, б). У цьому випадку будь-яка частинка рідини знаходиться під дією прискорень а та g, отже проекції результуючої одиничних масових сил будуть наступними; Х = -а, Y = 0, Z = -g. Підставляючи ці значення в (7), отримаємо:

-adx - gdz = 0,

або після інтегрування,

ax + gz = cоnst.

Це рівняння похилої площини. Отже, в даному випадку поверхні рівного тиску є площини, які похилі до осей 0х і 0z і паралельні осі 0у. Кут нахилу площини до горизонту:

β = arctg (a / g).

Приклад 3. При обертанні рідини разом із циліндричною посудиною відносно її вертикальної осі симетрії з постійною кутовою швидкістю її поверхня під впливом відцентрових сил приймає форму параболоїда обертання АВС (рис. 6), висота Н якого визначається по формулі

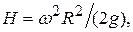(8)

а об’єм параболоїда

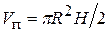(9)

Коли при обертанні рідини її вільна поверхня перетинає дно посудини (рис. 7), показаний об’єм рідини можна обчислювати двояко:

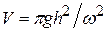або (10)

Рис. 6 Рис. 7

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Алгоритм розрахунку температури поверхні чипу ІМС процесора
3. Асимптотичний підхід до порівняння оцінок
4. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
5. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
6. Вивід основного рівняння фільтрації
7. Визначення температури на поверхні ізоляції принадземномупрокладанні та при прокладанні трубопроводів в приміщенні.
8. Вимірювання розмірів деталей та шорсткуватості поверхні
9. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
10. Головне рівняння відцентрового насоса. Теоретичний напір.
11. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.
12. Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.

Переглядів: 2941