• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основне рівняння гідростатики.

З метою приведення рівняння Ейлера до виду, зручного для інтегрування, помножимо кожне рівняння відповідно на dx, dy, dz і складемо почленно:

.

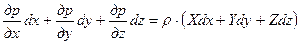Тому, що гідростатичний тиск залежить тільки від незалежних перемінних координат x, y, z, ліва частина цього рівняння являє собою повний диференціал функції р = f(x, y, z):

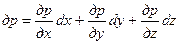
Виконуючи підстановку, отримуємо остаточно

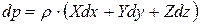. (5)

Отримане рівняння називається основним диференціальним рівнянням гідростатики. Рівняння виражає функціональну залежність тиску від роду рідини і координат точки в просторі.

Рис. 4 Графічна ілюстрація основного рівняння гідростатики.

Розглянемо найбільш важливий для практики випадок рівноваги рідини, що знаходиться в абсолютному спокої. Припустимо, що закритий резервуар заповнений рідиною, яка знаходиться у спокої. Будемо вважати, що на поверхні рідини діє відомий нам тиск р_{0 ,} відмінний від атмосферного. Тоді проекції об'ємних сил (у даному випадку сили ваги) на вісі x і y будуть дорівнювати нулю:

X=Y=0.

Проекція сили тяжіння на вісь z буде дорівнювати Z = -g. Таким чином, основне диференціальне рівняння гідростатики для розглянутого випадку прийме наступний вигляд:

, чи .

Отримане рівняння є диференціальним рівнянням рівноваги рідини, що знаходиться під дією тільки сили тяжіння. Після інтегрування рівняння отримаємо:

.

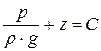Знайдемо постійну інтегрування. На поверхні рідини (вільній поверхні) нам відомо, що: р=р₀ і z=z₀, тобто відомі граничні умови. У такий спосіб для вільної поверхні:

.

Підставимо значення константи С і отримаємо

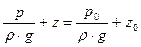, чи р=р₀+ρ·g(z₀-z),

тобто величина гідростатичного тиску цілком визначається вертикальною координатою точки або глибиною її занурення під поверхнею з відомим на ній тиском.

Розглянемо в рідині вільну точку А з координатою z і глибиною занурення h. Вважаючи, що h=z₀-z, можемо написати основне рівняння гідростатики в найбільш зручній формі:

р=р₀+ρgh, (6)

де р – повний гідростатичний тиск, який дорівнює тиску на вільній поверхні р₀, який складений з так званим тиском, обумовленим вагою самої рідини.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Асимптотичний підхід до порівняння оцінок
3. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
4. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
5. Вивід основного рівняння фільтрації
6. Видоутворення як основне явище еволюційного процесу.
7. Вступ. Здоров’я як проблема. Здоров’я - основне поняття
8. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
9. Головне рівняння відцентрового насоса. Теоретичний напір.
10. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.
11. Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
12. Динамічна інтерпретація диференційного рівняння другого порядку. Консервативні системи.

Переглядів: 2201