• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Неперервні розподіли

1. Рівномірний розподіл на відрізку

Щільність розподілу ймовірностей

(34)

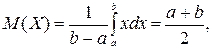
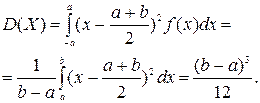
2. Нормальний (чи гаусовський) розподіл.

Щільність розподілу ймовірностей має вигляд

(35)

де - середнє квадратичне відхилення. Математичне сподівання

Вважаючи і застосовуючи формулу інтегрування частинами, одержимо

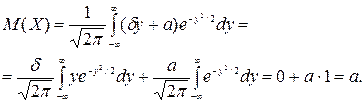
Оскільки функція - непарна, а 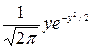є щільністю нормального розподілу з параметрами (0;1), то перший інтеграл у правій частині останньої формули дорівнює 0, а другий а. Таким чином, якщо ВВ Х розподілена нормально з параметрами 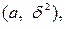то М(Х)=а. Дисперсія

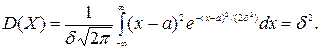
При обчислені М(Х) і D(X) використовувався інтеграл Пуассона:

.

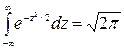Якщо ВВ X має нормальний розподіл з параметрами М(Х) = а і 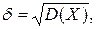то символічно це записують ВВ 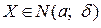. Графік щільності розподілу ймовірностей, який задають формулою (2.3), називають нормальною кривою чи кривою Гауса. Нормальна крива – це колоколоподібна крива, симетрична відносно прямої 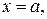яка асимптотично наближається до осі абсцис при 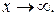Приведемо без доведення основні властивості кривої Гаусса.

1. Функція щільності розподілу ймовірностей визначена для будь-якого

2. Крива Гаусса розташована над віссю Ох для будь-якого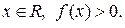

3. Вітки кривої Гаусса асимптотично наближаються до осі Ох

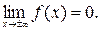
4. Крива Гаусса має максимум у точці 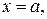рівний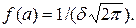

5. Крива Гаусса симетрична відносно прямої

Отже, для ВВ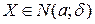 математичне сподівання збігається з модою і медіаною розподілу.

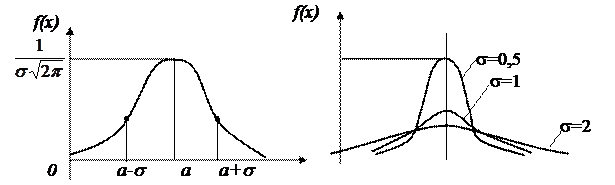
На рисунку зображені криві Гаусса при і 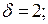1; 0,5; зміна параметра 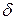при фіксованому значенні а характеризує форму кривої Гаусса.

За нормальним законом розподілу розподілено багато неперервних ВВ, що зустрічається в техніці: помилки виміру, висота мікронерівностей на обробленій поверхні, відхилення розмірів деталей від номінального, амплітуди коливання машин, які виникають при русі.

Ймовірність попадання ВВ X, розподіленої нормально, в заданий інтервал 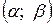обчислюється за формулою

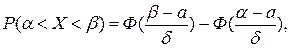(36)

де 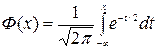- функція Лапласа.

Ймовірність того, що абсолютна величина відхилення ВВ Х від свого математичного сподівання менше будь-якого

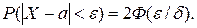
Приклад 23. Бракування кульок для підшипників відбувається в такий спосіб: якщо кулька не проходить через отвір діаметром , але проходить через отвір 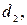то його розмір вважається прийнятним. Якщо яка-небудь з цих умов не виконується, то кулька бракується. Відомо, що діаметр кульки D є ВВ із характеристиками 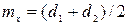і 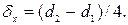Визначити ймовірність P того, що кулька буде забракована.

Розв’язування. Маємо:

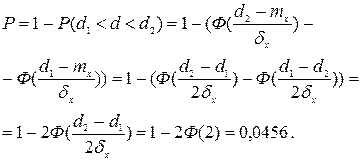
Читайте також:

1. Ве­личи­ни та її вла­с­ти­во­с­ті. Дискретні випадкові величини та їх розподіли
2. Двовимірні неперервні випадкові величини
3. Дискретні і неперервні випадкові величини
4. Дискретні розподіли
5. Лекція 6 Неперервні випадкові величини та їх розподіли
6. Неперервні випадкові величини
7. Неперервні випадкові величини
8. Тема 10. Неперервність функції в точці
9. Теорема Кантора про рівномірну неперервність функції.
10. Теорема про неперервність оберненої функції.
11. Точні вибіркові розподіли. Точкові і інтервальні оцінки

Переглядів: 1027