• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Диференційне рівняння теплопровідності

Рівнянням (9), тобто законом Фур’є в прямій формі не можливо скористатись не знаючи закону розподілу температури в середовищі, а відповідно величини градієнту температури 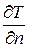. Відповідь на це питання дає диференційне рівняння теплопровідності, яке виводиться з рівняння теплового балансу і рівняння Фур’є, що розглядаються в межах елементарного об’єму .

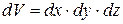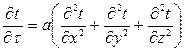В кінцевій формі (вивід є в рекомендованій літературі) рівняння приймає вигляд

(11)
де 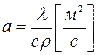- коефіцієнт температуропроводності, 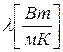, , 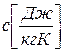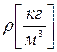вже відомі нам коефіцієнт теплопровідності, теплоємність і густина речовини.

Величини 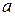характеризує тепло інерційні властивості тіла. Із збільшенням 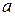зміна температури ( 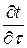) в часі також зростає.

Вираз називають оператор Лапласа.

Для випадку, коли температура змінюється тільки в одному напрямку (називається одномірною задачею), рівняння(11) спрощується

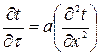(12)

Рівняння (11) ще більше спрощується для стаціонарного процесу, коли . Оскільки фізична константа , то рівняння (11) остаточно приймає вигляд

(13)

Це рівняння слід розв’язувати при заданих граничних умовах.

Розглянемо конкретну задачу – теплопровідність плоскої стінки.

Граничними умовами є

x=0 t=t_ст.1 (14)

x= t=t_ст.2 (15)

Після інтегрування (13) враховуючи, що в даному випадку часткова похідна співпадає з повною отримаємо

(16) (17)

Підставляючи граничні умови (14) та (15) в рівняння (16) і (17) отримаємо рівняння, яке визначає градієнт температури

(18)

і рівняння, яке називається рівнянням теплопровідності плоскої стінки (19)

(19)

або

(20)

Рівняння (19) і (20) дозволяють визначити кількість тепла Q і тепловий потік q для випадку теплопровідності плоскої стінки в стаціонарних умовах.

Якщо рівняння (20) представити у вигляді

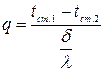і порівняти його із законом Ома, що визначає силу струму

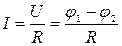, де 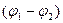- різниця потенціалів ( або рушійна сила), R – опір провідника, то видно їх тотожність. За аналогією знаменник 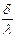називають термічним опором стінки (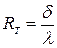). Якщо стінка складається з декількох шарів, наприклад, стальний апарат емальований зсередини, а зовні покритий тепловою ізоляцією, то опори сумуються (як при послідовному з’єднанні провідників)

(21)

В цьому випадку рівняння теплопровідності плоскої стінки (21) буде мати вигляд

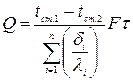(22)

Якщо стінка має циліндричну форму (трубопроводи, покриті тепловою ізоляцією) при співвідношенні , розподіл температури по товщині стінки буде підпорядковуватись вже не лінійному, а логарифмічному закону (в зв’язку з тим, що тепловий потік – постійна величина, а поверхня 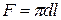- змінюється із зміною ), рівняння теплопровідності циліндричної стінки отримає вигляд

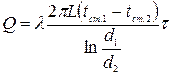(23)

Для багатошарової стінки:

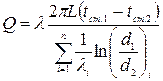(24)

де 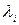- коефіцієнт теплопровідності -го шару, 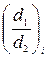- співвідношення цього шару.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Асимптотичний підхід до порівняння оцінок
3. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
4. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
5. Вивід основного рівняння фільтрації
6. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
7. Головне рівняння відцентрового насоса. Теоретичний напір.
8. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.
9. Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
10. Динамічна інтерпретація диференційного рівняння другого порядку. Консервативні системи.
11. Диференціальне рівняння
12. Диференціальне рівняння Ейлера для потоку рідини.

Переглядів: 3023