• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Диференційне рівняння конвективного теплообміну.

Для того, щоб зрозуміти механізм розрахунку коефіцієнта тепловіддачі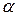слід розглянути диференційне рівняння конвективного теплообміну, яке описує швидкість зміни температури в рухомому середовищі за рахунок одночасного переносу тепла конвекцією і теплопровідністю.

Диференційне рівняння конвективного теплообміну

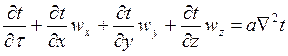(6)

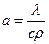– коефіцієнт температуропровідності,

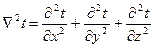– оператор Лапласа.

Рівняння (6) ще називають рівнянням Фур’є – Кірхгофа. Рівняння (6) показує залежність розподілу температури в потоці теплоносія одночасно за рахунок теплопровідності і конвекції.

Якщо процес теплообміну буде встановленим (стаціонарним) складова .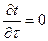

З рівняння (6) легко отримати диференційне рівняння теплопровідності для нерухомого середовища, якщо враховувати, що тоді

W_Х=W_Y=W_Z=0.

Для розв’язку рівняння (6) має бути доповнене диференційним рівнянням Нав’є–Стокса, що описує гідродинаміку потоку реальної рідини, а також початковими та граничними умовами. Така складна система диференційних рівнянь в загальному випадку розв’язку не має, оскільки в рідині, що рухається турбулентно сама структура потоку складається з окремих вихрових утворень, що є нестійкими і які постійно змінюються, як по розмірах, так і по швидкості і напрямку руху.

Методична цінність цього рівняння в тому, що за його допомогою виявляються складові, що визначають критерії теплової подібності, як співвідношення відповідних сил або інтенсивності перенесення.

Критерії теплової подібності

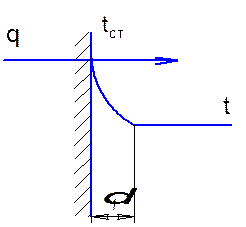
Якщо розглянути густину теплового потоку на границі розподілу, (стінка–теплоносій) і визначити на основі рівнянь:

1) тепловіддачі – Ньютона;

2) теплопровідності Фур’є для пограничного шару, то отримаємо рівняння

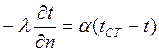(7)

Комплекс зліва враховує інтенсивність перенесення тепла в пограничному шарі теплопровідністю, а комплекс справа через рівняння Ньютона.

Якщо скористатись методами теорії подібності (тобто відкинути знаки диференціювання, а відношення зміни нескінченно малих величин замінити відношенням самих величин), то отримаємо перший тепловий критерій Нусельта 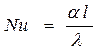, який визначає міру відношення конвективного теплообміну до кондуктивного (шляхом теплопровідності) в пограничному шарі на границі стінка-теплоносій. Цей критерій є визначуваним, який залежить від інших, що його визначають. З критерію Nu визначають коефіцієнт тепловіддачі α.

В критерій Nu входять α-коефіцієнт тепловіддачі, l-характерний геометричний розмір поверхні (наприклад, при русі в трубі це d-діаметр труби), λ-коефіцієнт теплопровідності теплоносія.

З рівняння (6) отримують такі критерії теплової подібності

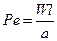– критерій Пекле, що характеризує міру відношення конвективного до кондуктивного теплообміну в ядрі потоку теплоносія .

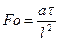– критерій Фур’є, критерій що враховується в нестаціонарних процесах, як міра співвідношення теплоти, що переноситься теплопровідністю і пульсаціями потоку в умовах нестаціонарного руху.

Критерій Пекле можна розписати як

; ;

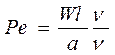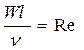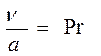
Re – критерій Рейнольда

Рr – критерій Прандтля, можна ще розписати, записавши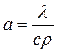

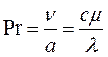
Рr – це міра співвідношення в’язкісних і температурних властивостей теплоносія, які формують гідродинамічний і тепловий пограничний шари.

Критерій Аr для співвідношення сил тертя та підйомних сил в умовах теплообміну можна трансформувати у критерій Gr (Грасгофа) де конвекція забезпечується різницею густин внаслідок різниці температур і відповідно температурного розширення. (t_ст–t)=Δt

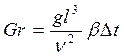
β – коефіцієнт температурного розширення.

В загальному випадку залежність теплообміну має вигляд

Nu=f(Re, Pr, Gr, Fo, Г...) (8)

Г – це геометрична подібність, для різних випадків 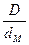(D – діаметр апарату, d_M – діаметр мішалки), 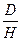(D – діаметр, Н – висота), і т.д.

Критеріальні рівняння представляють у степеневому вигляді, при чому виділяють критерії, що найбільше впливають в кожному конкретному вигляді, а коефіцієнт А і показники степені визначають в результаті узагальнення дослідних даних.

Наприклад: для встановленого потоку при вимушеному русі теплоносія критеріальне рівняння має вигляд

Nu=A·Reⁿ∙Pr^m (9)

A, n, m залежать від режиму руху (ламінарний або турбулентний), форми тіла (геометрії потоку) і напрямку потоку, відносно твердої поверхні.

Критеріальних рівнянь типу (9) отримано багато, вони розрізняються певними умовами тепловіддачі і їх вибирають з довідника (Павлов, Романков, Носков).

Приведемо тільки один приклад, що найбільш широко використовується

Nu=0,021· Re^0,8∙Pr^0,43(Pr/Pr_ст)^0,25

цей випадок відповідає тепловіддачі при русі теплоносія в трубі при Re>10⁴.

Певні особливості має тепловіддача при зміні агрегатного стану – конденсації або кипінні, але і в цьому випадку отримані критеріальні рівняння, що визначають відповідні значення критерію Nu, або в кінцевому випадку коефіцієнта тепловіддачі α.

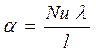
Алгоритм розрахунку α

1. Уточнюють умови протікання процесу, визначають фізико-хімічні параметри (μ, ρ, λ, с, β...) при середній температурі теплоносія і біля стінки, геометричні характеристики для потоку і режим руху (Re).

2. З літературних джерел вибирають відповідне до умов п.1 критеріальне рівняння.

3. Розраховують необхідні критерії (Re, Re_CT, Pr, Gr…)

4. Визначають критерій Nu, а з нього коефіцієнт тепловіддачі .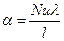

Основне рівняння теплопередачі. Визначення коефіцієнта теплопередачі.

Основне рівняння теплопередачі

Q = k∙F∙Δt_cp (10)

ми вже розглянули. Але щоб ним користуватись, слід вміти визначити k– коефіцієнт теплопередачі [Вт/(м²К)], і середню рушійну силу Δt_cp.

Механізм процесу теплопередачі через стінку

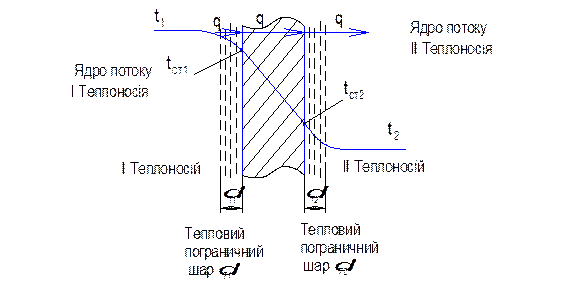
Якщо розглянути густину теплового потоку на вказаних ділянках і врахувати що це один і той самий потік отримаємо рівність

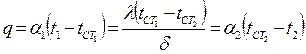(11)

Розв’язуючи рівняння (11) відносно різниці температур теплоносіїв (t₁-t₂) одержимо

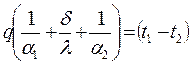(12)

суму величини в дужках позначимо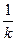

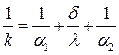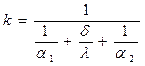або (13)

k – коефіцієнт теплопередачі

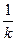– сумарний термічний опір теплопередачі, який складається з опорів стінки 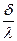і двох пограничних шарів для відповідних теплоносіїв 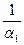і .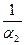

Якщо на стінці відкладені накип, ржа, забруднення, або нанесені емаль і т.д. ці опори сумуються .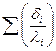

Таким чином, коефіцієнт теплопередачі визначається за рівнянням

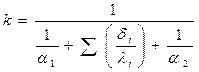(14)

Основна задача інтенсифікації теплопередачі це збільшення коефіцієнта теплопередачі k, а для цього треба зменшити відповідні термічні опори.

Наприклад, якщо опір стінки значно менший і ним можна знехтувати

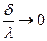, то .

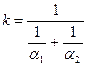Якщо α₁≈10÷20, а α₂≈10⁴÷2∙10⁴, то 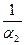<<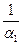і процес в цілому визначається тепловіддачею до стінки, тобто k≈α₁.

Тут для інтенсифікації процесу в цілому слід збільшувати α₁ (за рахунок турбулізації потоку, оребрення стінки і т.д.), тобто менше значення α₁.

Якщо великий опір створює стінка слід її очистити від накипу, ржі і бруду. Для цього використовують механічні і хімічні методи.

Для орієнтиру, які значення має коефіцієнт тепловіддачі при різних випадках слід орієнтуватись на табл. 4.7.(Павлов, Романков, Носков).

Наприклад

α_гази ≈ 35÷60 (вимушений рух)

α_вода ≈ 1200÷5800 (вимушений рух)

α_{конд насич пари} ≈ 9300÷15000

α_{орган рідин} ≈ 250÷800

В табл. 4.8. представлені орієнтовні значення коефіцієнтів теплопередачі при комбінації відповідних теплоносіїв.

Визначення середньої рушійної сили Δt_ср

Рушійною силою при теплопередачі є різниця температур теплоносіїв (t₁-t₂). Оскільки один із теплоносіїв може охолоджуватись, а другий відповідно нагріватись, то ця різниця по довжині теплообмінника буде змінюватись. Як наслідок в розрахунки вводять Δt_ср. Формула для розрахунку Δt_ср виводиться в залежності від напрямку руху теплоносіїв. Тут розрізняють такі випадки:

1) прямотечійний, коли обидва теплоносії рухаються в одну сторону

схематично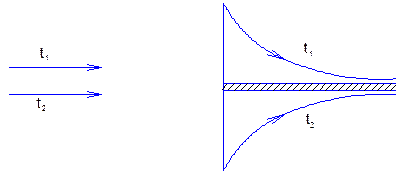

2) протитечійний, коли теплоносії рухаються в протилежному напрямку

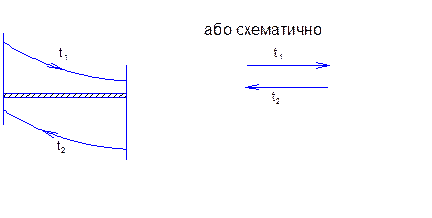
3) перехресний рух, схематично

t₁

t₂

4) комбіновані варіанти руху, коли напрямки частково співпадають і частково протилежні

приклад

Опускаючи вивід рівняння для визначення Δt_ср запишемо кінцеві формули

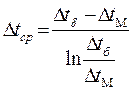
де для прямотечії

Δt_δ=t_1n-t_2п Δt_м=t_1k-t_2k.

для протитечії

Δt_δ=t_1n-t_2k Δt_м=t_1k-t_2n

Якщо 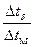< 2 формула для розрахунку Δt_ср спрощується і визначається як середньоарифметична

Δt_ср=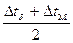 (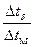< 2)

Слід зазначити, що протитечійний рух має перевагу над іншими напрямками з позицій величини Δt_ср, а відповідно інтенсивності теплопередачі.

Як приклад, оцінимо Δt_ср для прямотечії і протитечії, коли кількість тепла що передається, витрата і температури на вході і виході однакова, тобто з теплового балансу

Q = G₁ с₁ (t_1n-t_1k) = G₂ с₂ (t_2k-t_2n)

величини співпадають.

Розрахуйте рушійну силу самостійно

100 60 100 60

10 50 50 10

Δt_δ=100-10=90 Δt_м=60-50=10º

Δt_ср-? порівняти Δt_ср-?

Для перехресного і комбінованого напрямків руху, Δt_ср розраховується як для протитечії, але потім множиться на поправочний коефіцієнт < 1, який вибирається графічно з рисунків в залежності від напрямку і двох параметрів P і R, які розраховуються

;

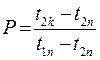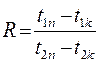
(Рис.VІІІ Павлов, Романков, Носков).

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Асимптотичний підхід до порівняння оцінок
3. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
4. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
5. Вивід основного рівняння фільтрації
6. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
7. Головне рівняння відцентрового насоса. Теоретичний напір.
8. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.
9. Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
10. Динамічна інтерпретація диференційного рівняння другого порядку. Консервативні системи.
11. Диференціальне рівняння
12. Диференціальне рівняння Ейлера для потоку рідини.

Переглядів: 3153