
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Класичні методи: від античності до нового часу
Абетка
Елементарна криптографія
1.1. Початкові поняття та приклади.Класична задача криптографії постає тоді, коли двоє збираються обмінятися конфіденційною інформацією за присутності третьої недружньої персони, яка також намагається заволодіти цією інформацією. Підтримуючи усталену у криптографічній літературі традицію, ми назвемо двох перших осіб Алісою та Бобом. Третій персонаж називатиметься суперником. Аліса та Боб є законними користувачами каналу зв'язку або легальними абонентами комунікаційної мережі. Суперник є несанкціонованим користувачем, який має нешляхетну мету перехопити чи підслухати Бобове повідомлення Алісі. Аби зберегти таємницю, Боб шифрує своє повідомлення, тобто перетворює його до незрозумілої для суперника форми, застосувавши алгоритм шифрування. В результаті з повідомлення, яке ще називають відкритим текстом, виходить криптотекст, який Боб і посилає Алісі. Отримавши криптотекст, Аліса дешифрує його за допомогою алгоритму дешифрування і отримує вихідне повідомлення. В наших криптологічних студіях ми виходимо із припущення, що суперникові завжди щастить перехопити криптотекст. Проте якщо алгоритм шифрування є надійним, то суперник не здатен дошукатися змісту повідомлення.
Алгоритми шифрування та дешифрування разом складають криптосистему або, простіше, шифр.
Розглянемо приклад. Поставивши себе на місце суперника, уявимо що нам вдалося підслухати зашифроване повідомлення:
осіла унофелет од шидохдіп єн умоч
Спробуймо відновити повідомлення, відгадавши алгоритм шифрування. Поза сумнівом, успіх буде миттєвим1.
Шифр, з яким ми щойно ознайомились, має дві типові риси, бажану і небажану. Перша полягає в тому, що цей шифр є ефективним. Шифрування і дешифрування займають зовсім мало часу. Негативною рисою цього шифру є його ненадійність. Найчастіше вимоги, які висуваються до криптосистеми, не вдається задовольнити одночасно — ідеального шифру не існує. Вибір шифру з тими чи іншими властивостями диктується конкретною ситуацією. Іноді інформація, скажімо біржова, перестає бути таємною через двадцять хвилин і мусить бути зашифрована і передана за лічені секунди. А іноді інформація повинна зберігатись десятиліттями, зате нема потреби квапитись при шифруванні.
Розглянемо ще дві прості криптосистеми.
шифр цезаря. Давньоримський імператор Юлій Цезар (100-44 р. до н.е.) полюбляв зашифровувати свої таємні послання у спосіб, коли кожна буква заміщується деякою іншою, а саме тою, що знаходиться у алфавіті через три позиції. Стосовно української абетки це означає що, а міняється на г, б на ґ, в на д і т.д. Останні ж букви абетки ь, ю, та я зміщуються теж на три позиції циклічно, тобто переходять у а, б та в, відповідно. Для прикладу, слову імперія відповідає криптотекст лптзулв. Кажуть, що шифр Цезаря є шифром зсуву на 3 позиції.
шифр частоколу. Алгоритм шифрування найліпше пояснити на прикладі. Щоб зашифрувати повідомлення криптографія, переписуємо його у вигляді "частоколу" к р и п т о г р а ф і я і зчитуємо текст рядками, почавши з верхнього. В результаті отримуємо криптотекст рпорфякитгаі. "Висоту" частоколу можна вибирати. Щойно вона в нас була 2. Для висоти 3 ми на проміжному етапі мали б к р и п т о г р а ф і я , а остаточним результатом був би криптотекст игірпорфякта.
Довжина зсуву і висота частоколу у розглянутих шифрах є секретним ключем, який використовується як алгоритмом шифрування для перетворення відкритого тексту у криптотекст, так і алгоритмом дешифрування для зворотнього перетворення. Аліса та Боб домовляються про ключ завчасно (при особистій зустрічі, через надійного посередника тощо), зберігають його у таємниці і досить часто його міняють.
1Повідомлення записане назворот, тобто, його слід читати не зліва направо, а навпаки.
Ми описали найпростішу криптографічну ситуацію. Схематично вона зображена на малюнку 1. Літерами М та С на малюнку позначено відкритий текст та криптотекст, а літерою К — ключ. Літерами Е та D позначені алгоритми шифрування та дешифрування відповідно. Цих позначень ми будемо дотримуватись і надалі.
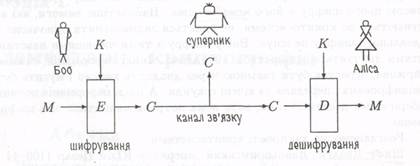
Малюнок 1. Класична криптографічна схема.
Те, що криптотекст С є результатом застосування алгоритму Е до відкритого тексту М та ключа К, записуватимемо як С= Ек(М). Подібним чином, запис М=Dк(С) означає, що М отримується із С та К за допомогою алгоритму D.
Аналізуючи надійність шифру, ми зобов'язані виходити із припущення, що суперник не лише здатен підслухати С, але й знає алгоритми Е і D; і тільки ключ К йому невідомий.
Для знаходження М суперник може скористатися методом повного перебору. Тобто, суперник може перебирати всі можливі ключі К і обчислювати Dк(С) доти, доки не натрапить на осмислений текст, який вірогідно і буде шуканим. Тому у надійної криптосистеми кількість можливих ключів мусить бути досить великою, щоб повний перебір не можна було зробити ні за який розумний час навіть з використанням швидкодіючої обчислювальної техніки.
Зауважимо, що знаходження ключа не є єдино можливим способом досягти успіху суперникові. Прикладом може служити частотний метод, описаний у пункті 2.2 цього розділу.
Якщо суперникові пощастило віднайти спосіб знаходження повідомлення за криптотекстом, то кажуть, що він розкрив шифр. Криптографія є мистецтвом створення шифрів, а криптоаналіз — їх розкриття. Тож респектабельніше називати суперника криптоаналітиком. Криптографія та криптоаналіз — дві складові криптології. Зрозуміло, що поділ дещо умовний, адже криптограф не може бути впевненим у надійності шифру без проведення його криптоаналізу. У ширшому трактуванні, завдання криптоаналізу не лише ламати шифри, тобто доводити їх ненадійність, але й навпаки, доводити у вигляді математичної теореми надійність шифру, попередньо означивши, який саме шифр слід вважати надійним.
Отже, перед криптоаналітиком стоїть завдання відновити повідомлення М. Згідно із традиційною термінологією, він проводить атаку на шифр. Так метод повного перебору ключів, ми будемо називати також брутальною атакою. Для розв'язування свого завдання криптоаналітик може мати різні передумови. Для останніх прийнята така класифікація.
Атака лише із криптотекстом. Суперник знає лише криптотекст Ек(М). Досі саме така ситуація і малася на увазі. У гіршому випадку (кращому з погляду суперника), крім Ек(М) відома ще певна кількість криптотекстів Ек(М1),.. .,Ек(Мl), зашифрованих з використанням одного й того ж ключа.
Атака з відомим відкритим текстом. Крім Ек(М) суперник знає як додаткові криптотексти Ек(М1),.. .,Ек(Мl), так і відповідні їм відкриті тексти М1,.. ., Мl, (які, скажімо, пересилалися раніше і з тих чи інших причин вже не є таємними).
Атака з вибраним відкритим текстом. Суперник має доступ до "шифруючого устаткування" і спроможний отримати криптотексти Ек(М1),.. .,Ек(Мl) для вибраних на власний розсуд відкритих текстів М1,.. ., Мl 2
Атака з вибраним криптотекстом. Суперник має доступ до "дешифруючого устаткування" і спроможний отримати відкриті тексти Dк(М1),.. .,Dк(Мl) для вибраних на власний розсуд криптотекстів C1,.. ., Cl (однак, як і у випадку попередньої атаки, неспроможний отримати безпосередньо таємний ключ).
Якщо атака певного виду призводить до розкриття шифру, то шифр є вразливим до неї; якщо ж ні, то шифр є стійким до такого виду атаки.
2 Ця атака відповідає мінімальним можливостям суперника у випадку криптосистем з відкритим ключем, яким присвячено розділ V.
1.2. Термінологічні застереження.Як зазначалось, криптологія є наукою, яка поділяється на криптографію та криптоаналіз. Однак досить часто термін криптографія вживається у загальнішому розумінні як синонім до криптології. 3аxucm інформації є ширшою галуззю, що охоплює крім теоретичних основ також технічні засоби, юридичні аспекти тощо.
Тайнопис також є ширшим поняттям. Крім криптографічних, він допускає й такі способи збереження таємниці, при яких повідомлення ніяк не перетворюється, а приховується сам факт його існування чи пересилання. Прикладом може служити використання невидимого чорнила.
Вживання термінів код та кодування як синонімів до шифру та шифрування є не лише архаїчним, а часто й помилковим. Код — це усталене правило для заміни одиниць інформації (букв, слів, цілих фраз) певними символами. Наприклад, SOS є кодом прохання про допомогу, а згідно із ASCII кодом літера а кодується двійковою послідовністю 1100001. Коди, які вивчає математична теорія кодування, застосовуються з метою дещо протилежною до криптографічної. Повідомлення шифрується для того, щоб воно стало незрозумілим, а кодується для того, щоб бути зрозумілим навіть після часткового спотворення із-за природних перешкод у каналі зв'язку. Ці два терміни слід чітко розмежовувати тому, що на практиці одна й та ж інформація може підлягати обом діям — у типовій ситуації текст закодовують у двійкову послідовність, її шифрують, а отриманий криптотекст перед відправленням кодують за допомогою коду, який дозволить виправити помилки після передачі.
Як рівноправні терміни ми будемо вживати дієслова шифрувати і криптувати та віддієслівні іменники шифрування і криптування. Виключно справою смаку є вибір між словосполученнями розкрити криптосистему та зламати криптосистему. Нарешті, термін криптотекст має синонім криптограма, який щоправда зустрічається частіше у популярній, ніж у фаховій літературі.
1.3. Ретроспективні зауваження.Першим шифром, про який збереглася згадка, вважається шифр Скитала, який використовувався спартанцями для військових донесень у V ст. до н.е. Скиталою називався дерев'яний валик, на який щільно намотувалась стрічка пергаменту або шкіри. Повідомлення писалося рядками поздовж поверхні так, щоб у рядку на один звій припадала лише одна буква. Знята з валика стрічка містила незрозумілу послідовність букв, яку можна було прочитати лише знову намотавши стрічку на валик такого ж діаметру. Таким чином, ключем у цьому шифрі слугував діаметр валика.
Криптоаналіз відкрили араби. Опис частотного методу є у їхніх писемних джерелах початку XV століття.
Шифри, які використовувались починаючи від античних часів і аж до середини XX століття, можна класифікувати як шифри перестановки або заміни. Скитала і шифр частоколу є прикладами шифрів перестановки — при шифруванні всі букви повідомлення зберігаються, лише розміщуються в іншому порядку. Шифр Цезаря є прикладом шифру заміни — кожна буква повідомлення замінюється деякою іншою. Шифрам перестановки та заміни присвячено наступний параграф цього розділу.
З сьогоднішніх позицій можна вважати, що аж до середини нашого століття у криптографії активно розвивались класичні методи. Так, знаменитий шифр часу II-ої світової війни Enigma можна трактувати як вдалу на тоді технічну реалізацію шифру Блеза де Віженера, французького криптографа XVI сторіччя. Все ж винахід телеграфу та радіо дав потужний поштовх дослідженням у царині криптології, адже при наявності у суперника відповідного обладнання підслуховування стало для нього зовсім необтяжливою справою. Шифр одноразового блокноту був винайдений у 1917 році інженером Гілбертом Вернамом з AT&T для застосування у телетайпній мережі. Цей шифр є абсолютно надійним, лише деякі обставини звужують сферу його застосування, як от необхідність мати безпечний канал для обміну довгим ключем.
Перша електронно-обчислювальна машина була сконструйована задля зламу шифру Enigma за участю видатного англійського математика Алана Тьюрінга. Поява обчислювальної техніки докорінно змінила критерії ефективності та надійності шифру. Шифр вважається надійним в обчислювальному сенсі, якщо його розкриття хоча в принципі й можливе, але навіть на найшвидшому комп'ютері вимагатиме нереального часу (роки, століття і т.д.), після завершення якого будь-яка таємниця стане неактуальною. Популярною криптосистемою, надійною саме в такому сенсі, є DES — стандарт шифрування даних прийнятий у Сполучених Штатах. Шифр одноразового блокноту та DES ми розглянемо нижче у § 3.
Початком сучасного етапу розвитку криптографії є 1976 рік. З'являються принципово нові криптографічні засоби, що дозволяє називати цей етап революційним. Давня задача збереження конфіденційності повідомлення знайшла нове елегантне розв'язання у концепції відкритого ключа. Кардинальна відмінність криптосистеми із відкритим ключем (за іншою термінологією, асиметричної системи) від системи "дореволюційного зразка" (симетричної системи) полягає в тому, що у криптосистемах з відкритим ключем процедура шифрування стає загальнодоступною, але це не
означає як у традиційних криптосистемах, що загальнодоступним є також дешифрування. Поняття ключа розбивається на дві частини: ключ відкритий, та ключ таємний. Загальновідомий відкритий ключ використовується для шифрування, але дешифрування може здійснити лише той, хто володіє таємним ключем. Криптосистеми з відкритим ключем є предметом розгляду у розділі V.
Озброєна новою концепцією, криптографія почала розв'язувати і нетрадиційні доволі софістичні завдання, як от підписування документів у електронній формі, жеребкування телефоном, поділ секрету між кількома особами тощо. Подібним задачам присвячено розділ VII.
ВПРАВИ
1.1.Користуючись шифром зсуву на 2 позиції, зашифрувати повідомлення рятуйтесь.
1.2. Розшифрувати криптотекст мнзалмхз, отриманий за допомогою шифру зсуву на 31 позицію (пригадаємо, що в українській абетці 33 літери).
1.3. Розшифрувати криптотекст, отриманий за допомогою шифру зсуву із невідомим ключем: а) бвсблбебвсб; b) мдодпдбдпндмд; с) фхлфлтлчл; d)тсжсусіьгос.
1.4. Зашифрувати повідомлення переховуватися за допомогою шифру частоколу висоти а) 2; b) 3.
1.5. Розшифрувати криптотекст нйеаінндо, якщо відомо, що застосовано шифр частоколу невеликої висоти.
1.6. При шифруванні повідомлень записуванням їх назворот деякі повідомлення залишаються без зміни, як наприклад, кіт втік (пропуски між словами ігноруються). Тексти з такою властивістю називаються паліндромами. Скільки є паліндромів, які складаються з п букв української абетки
(не обов'язково змістовних)?
ЛІТЕРАТУРА
Канонічним джерелом з історії криптографії є [108]. Цікаві зауваження ретроспективного характеру зроблено в оглядах [141, 131, 44]. Із доступних популярних видань можна порадити [23, 25]. Взаємозв'язки між криптографією і теорією кодування висвітлено в [52].
ЛЕКЦІЯ 2
У цьому параграфі ми розглянемо шифри перестановки та підстновки. Останні називають також шифрами заміни.
2.1. Шифри простої заміниперетворюють відкритий текст таким чином, що кожен символ замінюється на якийсь інший. При цьому однаковим символам у відкритому тексті відповідають однакові символи у криптотексті, а різним — різні. Ключем є табличка, що вказує в який саме символ переходить кожен символ відкритого тексту. Для прикладу, шифр Цезаря в українському алфавіті задається таким ключем:
абвггдебжзиіїйклмнопрстуфхцчшщьюя гґдебжзиіїйклмнопрстуфхцчшіцьюяабв
При шифруванні кожна буква, яка зустрічається у повідомленні, шукається у верхньому рядку і замінюється відповідною буквою із нижнього рядка (пропуски між словами та розділові знаки ігноруються). Наприклад, криптографія перетворюється у нуйтхсеугчкв.
Алгоритм шифру Цезаря підставляє замість кожної букви алфавіту деяку букву того ж алфавіту. Могла б здійснюватись підстановка будь-яких інших символів, скажімо, ієрогліфів або ж піктограм танцюючих чоловічків як у випадку, описаному Артуром Конан Дойлом у однойменному оповіданні [22]. Має бути зрозумілим, що використання екзотичних символів у криптотексті хіба що надасть шифрові підстановки романтичного присмаку, але не зробить його надійнішим. Тому надалі ми без втрати загальності будемо вважати, що повідомлення та криптотекст пишуться в одному й тому ж алфавіті.
Зробивши це припущення, ми можемо підрахувати кількість всіх можливих ключів. Зробимо це для української абетки. Ключ — це табличка, верхній рядок якої містить всі букви у алфавітному порядку, а нижній — теж всі букви, але довільним чином перемішані. Отже питання полягає в тому, скількома способами можна розмістити всі букви абетки у нижньому рядку. Міркуємо так. Для першої позиції букву можна вибрати 33-ма способами. Після того як вона вибрана, для другої позиції букву можна вибрати вже 32-ма способами, для третьої — 31-м способом і т.д. Для передостанньої позиції вибір здійснюється 2-ма способами, остання ж буква визначена однозначно. Загальна кількість
можливостей розмістити букви у всіх 33 позиціях дорівнює добутку 33 • 32 • 31 •.....• 2. Таким чином, загальна кількість ключів є 33!.
В загальному випадку, коли алфавіт налічує п символів, результатом такого ж підрахунку числа всіх ключів буде n!. Зауважимо, що серед цієї загальної кількості деякі ключі є непридатними для вжитку, як от тривіальний ключ, у якому нижній рядок збігається з верхнім.
Шифр зсуву є звуженням загального шифру заміни на сукупність лише п ключів, у яких нижній рядок є циклічним зсувом верхнього рядка. Ключ такого гатунку повністю визначається довжиною зсуву s. Можна вважати, що 0 < s < п, оскільки зсуви на s і на s + п позицій дають однаковий результат.
Інші підкласи шифру простої заміни розглядаються у § II.3.
2.2. Частотний аналіз.Як нам відомо з попереднього пункту, шифр заміни над n-символьним алфавітом має п! ключів. Для значень п=26, 33 (латинський та український алфавіти) це число є дуже великим. Для його оцінки можна скористатися варіантом формули Стірлінга, звідки для п = 26 отримуємо п > 1026. Число справді велике — нагадаємо, що наша планета існує лише 109 років, а наступний льодовиковий період очікується через 14000 років, тобто 4,41504 • 1011 секунд [137]. Це співставлення переконливо засвідчує безперспективність брутальної атаки на шифр заміни, однак цього недостатньо аби стверджувати, що він є надійним. Виявляється, успішний криптоаналіз можливий за допомогою частотного методу.
Частота символу у тексті дорівнює кількості його входжень у цей текст, поділеній на загальну кількість букв у тексті. Наприклад, частота букви а у тексті купила мама коника дорівнює 4l18=2l9, а частота пропуску між словами у цьому ж тексті дорівнює 2l18 = 1l9.
Для кожної мови справджується такий емпіричний факт:
| У досить довгих текстах кожна буква зустрічається із приблизно однаковою частотою, залежною від самої букви і незалежною від конкретного тексту. |
На підставі цього факту із кожним символом пов'язують деяке число, частоту цього символу в мові, з якою приблизно він зустрічається в кожному великому тексті цією мовою. Підрахунок частот символів .у мові здійснюють на основі вибраного навмання середньостатистичного тексту. У додатку А наведено таблички частот для української, російської та англійської мов.
Припустимо, що перехоплено довгий криптотекст (або послідовність багатьох коротких), отриманий за допомогою шифру заміни. Частотним методом можна здійснити дешифрування, навіть не знаючи ключа. Для цього обчислюють частоти кожного символу в криптотексті і порівнюють отримані результати з табличкою частот для мови, якою написане повідомлення. Не слід сподіватися, що таким чином можна буде однозначно встановити ключ, але перебір це дозволить скоротити радикально. Наприклад, якщо при шифруванні не ігноруються пропуски між словами, то найпоширеніший символ у криптотексті поза сумнівом відповідає саме пропуску. А відтак стає відомою сукупність символів, що відповідають словам з одної букви (в українській мові це а,б,в,б,ж,з,і,й,о,у,я) та словам з двох букв (це, не, на, до та інші), що дозволяє ці символи розпізнати ціною справді невеликого перебору. Свою роль при частотному аналізі відіграє та обставина, що кожна мова володіє властивістю надлишковості, тобто текст можна поновити навіть коли частина його букв невідома.
Миттєвою є користь від частотного аналізу при розкритті шифру зсуву. Проілюструємо загальну ідею таким прикладом. Нехай нам належить розшифрувати криптотекст пщіспофнпмгашибгпефрптмбвмєоп, який був отриманий шифром зсуву, причому пропуски та розділові знаки ігнорувались. Підраховуємо частоти і зауважуємо, що найбільша, а саме 9l29, припадає на літеру п. Природньо припустити, що у відкритому тексті їй відповідає найпоширеніша в українській мові літера о. Це означало б, що довжина зсуву дорівнює 1. Виконуємо обернений зсув, тобто на одну позицію вліво, і справді отримуємо змістовне повідомлення, що охоронумолокозаводупослаблено.
Гомофонний шифр заміни був винайдений великим німецьким математиком Карлом Фрідріхом Гаусом [141]. Цей шифр грунтується на ідеї, яка робить підрахунок частот символів безперспективним. Кожна буква відкритого тексту замінюється не єдиним символом як у шифрі простої заміни, а будь-яким символом із декількох можливих. Наприклад, замість а може здійснюватись підстановка будь-якого із чисел 10,17,23,46,55, а замість б — будь-якого із 12,71. Головне, щоб замість різних букв завжди підставлялись різні символи — ця вимога забезпечує можливість дешифрування. Вибір одного з можливих варіантів щоразу робиться випадково. Якщо кількість варіантів для кожної букви пропорційна її частоті в мові, то всі символи у досить довгому криптотексті зустрічатимуться з приблизно однаковою частотою, що не дозволить пов'язати їх з якимись буквами відкритого тексту. Однак гомофонний шифр піддається ретельнішому і трудомісткішому різновиду частотного аналізу, який окрім частот окремих символів враховує також частоти пар символів. Подібний аналіз дозволяє ламати ще один клас шифрів заміни, про що йдеться у наступному пункті.
Частотний аналіз може бути корисним і в інших ситуаціях. Наприклад, він дозволяє комп'ютерові без участі людини відрізнити осмислений текст від хаотичного набору символів.Завдяки цьому на машину можна перекласти здійснення брутальної атаки, тобто повного перебору ключів.
2.3. Поліграмні шифри.Послідовність кількох букв тексту називається полігграмою. Послідовність із двох букв називається біграмою (іноді диграфом), а із l букв — l-грамою. 3- і 4-грами називають відповідно три- і тетраграмами3. Поліграмний шифр заміни полягає у розбитті відкритого тексту на l-грами для деякого фіксованого числа l і заміні кожної з них на якийсь символ чи групу символів. Ключем є правило, за яким відбувається заміна. Якщо загальна кількість символів у тексті не ділиться націло на l, то остання група символів доповнюється до l -грами довільним наперед обумовленим способом.
Як приклад розглянемо біграмний (часом кажуть диграфний) шифр, який назвемо шифром чотирьох квадратів, хоча насправді він є відміною відомого шифру Playfair (початок XVI століття). Цей шифр застосовується до текстів латинкою. Точніше, ми нехтуємо літерою j, яка найрідше зустрічається в англомовних текстах, і працюємо з 25-літерним алфавітом4. Ключем є чотири квадрати розміру 5 на 5, кожен з яких сформований із всіх 25 букв, розташованих у довільному порядку- Зручно розмістити ці чотири квадрати так, щоб вони утворювали один великий квадрат як у прикладі на малюнку 2.
Перед шифруванням із повідомлення вилучаються всі розділові знаки, пропуски між словами, а також літера j, після чого повідомлення розбивається на біграми. Кожна біграма заміщується деякою іншою, яка визначається за таким правилом. Перша буква біграми, що підлягає заміщенню, відзначається у верхньому лівому квадраті, а нижня друга — у нижньому правому. Далі беруться дві букви, одна у верхньому правому, а друга у нижньому лівому квадратах, так, щоб разом з двома відзначеними буквами вони утворювали вершини прямокутника. Саме ці дві букви є біграмою, яка з'являється у криптотексті. На-І приклад, при використанні ключа, зображеного на малюнку 2, біграмаї сг замінюється біграмою то, а слово cryptography перетворюється у mopwtiomfxns.

Малюнок 2. Приклад ключа для біграмного шифру чотирьох квадратів.
Інші приклади поліграмних шифрів, які оперують l-грамами для довільного фіксованого l, є предметом розгляду в § II.З.
Зрозуміло, що для поліграмних шифрів при l > 1 підрахунок частот окремих букв алфавіту нічого не дає. Однак для l = 2 з успіхом застосовується аналіз частот біграм. У додатку А наведено найпоширеніші в українській мові біграми.
2.4. Поліалфавітні шифриможна потрактувати як такі шифри заміни, в яких позиція букви у відкритому тексті впливає на те, за яким саме правилом ця буква буде змінена. Ми розглянемо два класичні приклади.
шифр віженера. Відкритий текст і криптотекст записуються в одному й тому ж алфавіті. Для букв x та у цього алфавіту5 означимо їх суму х + у як результат циклічного зсуву букви х вправо у алфавіті на кількість позицій, що дорівнює номеру букви у в алфавіті. При цьому Дотримуємося такої домовленості:
3 Терміни монограма і пентаграма випадають із цього ряду, бо мають інші значення.
4 Та й до середніх віків буква j в латинській абетці була відсутня.
5 Символами х та у ми позначаємо тут будь-які букви довільного алфавіту, а не лише латинські літери х та у.
| нумерація букв алфавіту починається з нуля. |
Наприклад, для української абетки маємо а + а = а, б + а = б,в + б = я+в = б. Ця операція природним чином задається так званою таблицей Віженера, яка зображена на малюнку 3.
| а б в г ґ д е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а а б в г ґ д е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я б б в г ґ д е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а в в г ґ д е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б г г ґ д е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в ґ ґ д е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д д е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г ґ е е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д д є є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е ж ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є з з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж и и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з і і ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и ї ї й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і й й к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї к к л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й л л м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к м м н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л н н о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м о о п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н п п р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о р р с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о п с с т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о п р т т у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о п р с у у ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о п р с т ф ф х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о п р с т у х х ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о п р с т у ф ц ц ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о п р с т у ф х ч ч ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о п р с т у ф х ц ш ш щ ь ю я а б в г д е е є ж з и і ї й к л м н о п р с т у ф х ц ч щ щ ь ю я а б в г д е е є ж з и і ї й к л м н о п р с т у ф х ц ч ш ь ь ю я а б в г д е е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ю ю я а б в г д е е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь я я а б в г д е е є ж з и і ї й к л м н о п р с т у ф х ц ч ш щ ь ю |
Малюнок 3. Таблиця Віженера. Буква х + у знаходиться на перехресті рядка, що відповідає букві х, і стовпчика, що відповідає букві у.
Шифр Віженера застосовують до повідомлення, записаного в рядок без пропусків між словами та розділових знаків. Ключем є слово у тому ж алфавіті. Якщо ключ коротший за повідомлення, то його записують багато разів підряд доки не вийде рядок такої ж довжини. Рядок з розмноженим ключем розміщують під рядком з повідомленням, і букви, що опинилися одна над другою, додають. В результаті отримують ще один рядок тої ж довжини, який і є криптотекстом. Наприклад, шифрування наказу "бороніть королівну від ворогів" з ключем "ключ" відбувається так:
БОРОНІТЬКОРОЛІВНУВІДВОРОГІВ
ключключключключключключклю
ЛАОЇЮЦРФШАОЇЩЦАІҐНЗЯМАОЇНЦА
Результатом шифрування є нижній рядок.
Як бачимо, на відміну від шифру простої заміни при використанні шифру Віженера однаковим буквам у відкритому тексті можуть відповідати різні букви у криптотексті. Ця обставина безперечно ускладнює частотний криптоаналіз. Шифр Віженера кілька століть вважався надійним, поки у 60-их роках минулого століття офіцер прусського війська Касискі не виявив, що цей шифр все ж піддається частотному методу. Скористаємось попереднім прикладом для пояснення основної ідеї. Шифр Віженера влаштований так, що при довжині ключа 4 кожна з чотирьох підпослідовностей відкритого тексту перетворюється відповідно до деякого шифру зсуву (на 14, 15, 31 і 27 позицій). За умови, що текст досить довгий, всі чотири довжини зсувів знаходяться стандартним підрахунком частот букв у відповідних підпослідовностях криптотексту. Однак як визначити із криптотексту, що застосовано ключ довжини саме 4? При прискіпливішому погляді на криптотекст зауважуємо у ньому однакові шматки — триграма аої зустрічається тричі, а біграма ца двічі. Природньо припустити, що це зумовлене не випадковістю, а тим, що у відкритий текст у відповідних місцях входить одна й та ж триграма та біграма (справді, у нашому випадку це оро та ів). Те, що дві однакові поліграми відкритого тексту проявились у криптотексті, означає, що відстань між ними є кратною довжині ключа. Відстані між різними входженнями триграми аої дорівнюють 8 і 12. Звідси висновок, що довжина ключа має ділити обидва ці числа, тобто вона дорівнює 1, або 2, або 4, — і нам лишається випробувати лише три можливості, щоб знайти, яка з них в дійсності має місце.
Зрозуміло, що описана метода може розраховувати на успіх завжди, коли довжина тексту співвідносно із довжиною ключа є великою. За цієї умови слід сподіватись, що текст міститиме чимало однакових біграм та триграм, і частині з них відповідатимуть однакові біграми та триграми у криптотекті з тої причини, що відстань між ними пропорційна до довжини ключа.
ШИФР З АВТОКЛЮЧЕМ грунтується на ідеях Віженера і Кардано. Подібно до шифру Віженера, криптотекст отримують сумуванням відкритого тексту із послідовністю букв такої ж довжини. Однак тепер
цю послідовність формують хитріше — спершу записують ключ, а справа до нього дописують початковий відрізок самого відкритого тексту. Якщо розглянути той же приклад, то шифрування відбуватиметься так:
БОРОНІТЬКОРОЛІВНУВІДВОРОГІВ
КЛЮЧБРРОНІТЬКОРОЛІВНУВІДВОР
ЛАО Ї ОЩЗЛЮЩЗЛЩЩТВДЙЙТХРЮУДЩТ
ЛЕКЦІЯ 3
2.5. Шифрування блоками. Часто алгоритм шифрування буває призначений для перетворення послідовностей символів лише фіксованої довжини l. Коли ж потрібно застосувати його до більшого тексту, цей текст розбивають на блоки — групи по l символів, і кожен блок перетворюють окремо. Такі шифри називаються блоковими з періодом l. Якщо загальна кількість символів у тексті не ділиться націло на l то остання група символів доповнюється до повного блоку довільним наперед обумовленим способом.
Прикладом блокового шифру з періодом l може слугувати будь-який поліграмний шифр, що здійснює заміну l -грам. Стосовно термінології зазначимо, що під поліграмою розуміють послідовність літер деякої природної мови, в той час як блок може складатися із довільних символів, скажімо, цифр.
Шифр Віженера з фіксованою довжиною ключа l теж можна розглядати як блоковий шифр з періодом l.
2.6. Шифри перестановки зберігають всі букви відкритого тексту, але розміщують їх у криптотексті в іншому порядку. Прикладами шифрів перестановки, які нам вже зустрічалися, є шифр частоколу і Скитала. Це представники широкого підкласу шифрів перестановки, які називаються шифрами обходу. У якості ще одного типового прикладу розглянемо матричний шифр обходу. Повідомлення записується рядками у вигляді прямокутної матриці. Криптотекст формується зчитуванням букв із матриці у зміненому порядку, а саме, стовпчиками. При цьому послідовність, у якій зчитуються стовпчики, визначається ключем. Було поширеним задання ключа у вигляді ключового слова, легко запам'ятовувалось. Порядок зчитування стовпчиків збігався з алфавітним порядком букв ключового слова. Приклад наведено на малюнку 4.
G A R D E N Повідомлення:
4 1 6 2 3 5 DON’T PUT IT OFF TILL TOWORROW
D O N T P U Ключове слово
T I T O F F GARFEN
T I L L T O Криптотекст
M O R R O W OIIOTOLRPFTODTTMUFOWNTLR
Малюнок 4. Матричний шифр обходу.
Дещо відхиляючись від теми, необхідно зазначити, що в наш час вживання в якості ключа для будь-якого шифру зручних для запам'ятовування ключових слів, є досить ризикованим із-за словникової атаки. Найпростіший варіант цього методу криптоаналізу полягає в укладанні списку із, скажімо, 100000 найвживаніших ключових слів, включно із географічними назвами та екзотичними термінами. Рафінованіші версії включають лексику із вузькофахових публікацій автора повідомлення, послідовності із двох-трьох складів китайської мови тощо.
У якості ще одного прикладу шифру перестановки наведемо доволі відомий у популярній математиці шифр Кардано. Це блоковий шифр з періодом l = k2, де k парне число. Ключем є вирізаний з паперу в клітинку квадрат розміру k на k, що складається з k2 клітинок, четверту частину яких, цебто k2/4, прорізують. На малюнку 5 подано приклад для k = 4, причому квадрат розліновано пунктиром, а контури чотирьох прорізаних клітинок виділено суцільною лінією.
Нехай потрібно зашифрувати блок повідомлення, у якому k2 літер. Криптотекст записують на клітчастому папері у квадраті k на k. Процедура займає чотири кроки. На першому кроці на аркуш, на якому буде писатись криптотекст, накладають ключ і вписують перші k2/4 літер повідомлення у прорізані клітинки, починаючи з верхнього рядка. На другому кроці ключ повертають на 90о градусів за годинниковою стрілкою відносно центру квадрату і у прорізані клітинки вписують наступні k2/4 літер повідомлення. Подібним чином виконують третій і четвертий кроки — щоразу ключ повертають на 90 градусів і у нові позиції прорізаних клітинок вписують чергові k2/4 літер повідомлення. Ключ має бути виготовлений у такий спосіб, щоб при повороті прорізані у ключі клітинки попали на вільні клітинки аркуша, і в жодному разі не наклалися на клітинки вже заповнені на попередніх кроках (див. вправу 2.22). В результаті після четвертого кроку всі k2 літер блоку повідомлення виявляються розміщеними в деякому порядку у квадраті k на k. Зчитавши їх рядками, отримують криптотекст. На малюнку 5 показано процедуру перетворення повідомлення мама мила раму рано у криптотекст рмрмиаааммлнуаоа.
Шифр Кардано є шифром перестановки спеціального виду, у якому правило переставлення букв у блоці зручне для реалізації на папері за допомогою ножиць та олівця. Загалбний шифр
перестановки l з періодом l переставляє l букв у довільному порядку, який визначається ключем.
 |
Ключ зручно задавати табличкою:


Малюнок 5. Шифр Кардано
яка показує, що перша буква блоку відкритого тексту займає позицію і1 у відповідному блоці криптотексту, друга буква переміщується на позицію і2, і т.д. Наприклад, при l = 4 шифр перестановки з ключем:
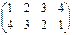
перетворює відкритий текст мамамиларамурано у криптотекст амамалимумаронар. А зображений а малюнку 5 ключ для шифру Кардано можна задати табличкою

Міркуваннями, подібними до викладених у пункті 2.1, легко довести, що шифр перестановки з періодом l має l! різних ключів. Якщо l є невеликим у порівнянні з довжиною тексту, шифр перестановки розкривається спеціальним чином організованим аналізом частот біграм. Як саме це відбувається, ми пояснимо на такому прикладі. Нехай маємо криптотекст
ІЦКАЗИВИМЯИЛКИНОЙРЕСРПІНЗМЕЛБОІШРПИИТИНИИВІСВИТАЛП і відомо, що він отриманий шифром перестановки з періодом 5. Розіб'ємо криптотекст на блоки по 5 букв і запишемо їх один під другим, розташувавши текст у десяти рядках та п'яти колонках як показано на малюнку 6.
| І | Ц | К | А | З | З | А | К | Ц | І | |
| И | В | И | М | Я |  Криптотекст Криптотекст
| Я | М | И | В | И |
| И | Л | К | И | Н | Відкритий текст
| Н | И | К | Л | И |
| О | Й | Р | Е | С | С | Е | Р | Й | О | |
| Р | П | І | Н | З | З | Н | І | П | Р | |
| М | Е | Л | Б | О | О | Б | Л | Е | М | |
| П | И | Р | П | И | И | П | Р | И | П | |
| И | Т | И | Н | И | И | Н | И | Т | И | |
| И | В | І | С | В | В | С | І | В | И | |
| И | Т | А | Л | П | П | Л | А | Т | И | |
 Номери стовпчиків Номери стовпчиків
|
Малюнок 6. Криптоаналіз шифру перестановки.
Зауважимо тепер, що дешифрування полягає у переставленні стовпчиків у належному порядку. Порядок цей, не знаючи ключа, можна становити такими міркуваннями. На першій і третій позиціях другого рядка стоїть літера и. Це означає, що перший і третій стовпчики не можуть стояти поруч, інакше ми мали б у відкритому тексті біграму ии, яка ніколи в українській
мові не зустрічається6 , навіть якщо з тексту вилучено пропуски між словами. Зауважуємо також подвійні входження літери и у третьому та сьомому рядках і потрійне входження у восьмому рядку. Беручи до уваги позиції букви и у цих рядках, приходимо до висновку, що не можуть знаходитись поруч 1-й і 4-й, 2-й і 5-й стовпчики, а також будь-які два із 1-го, 3-го та 5-го стовпчиків.
Неважко пересвідчитись, що ці вимоги задовольняють лише два розташування стовпчиків — (1,2,3,4,5) та (5,4,3,2,1). Оскільки перше розташування відповідає нашому криптотекстові, то для розташування стовпчків у відкритому тексті залишається єдина можливість — (5,4,3,2,1), щовідповідає ключеві:
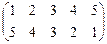
Здійснивши обернену перестановку, прочитуємо розшифроване повідомлення по рядках: З АКЦІЯМИ ВИНИКЛИ СЕРЙОЗНІ ПРОБЛЕМИ. ПРИПИНИТИ ВСІ ВИПЛАТИ!
У нашому криптоаналізі ми виходили з апріорно заданої інформаці що шифрування здійснювалось блоками довжини l = 5. Якби цього небуло відомо, належало б подібний аналіз проводити почергово для значень l = 2, 3,4,... аж поки б не було досягнуто успіху. Для максимально наочної ілюстрації загального принципу приклад був підібраний так, щоб| ключ було визначено однозначно на підставі єдиного факту — біграм ии зустрічається в українській мові з малою частотою (насправді нульовою). В загальному випадку беруть до уваги й інші малоймовір буквосполучення, і в результаті отримують систему обмежень на ключ яка як правило дозволяє суттєво скоротити перебір.
На завершення зробимо ще одне просте зауваження, корисне при атаці з відомим відкритим текстом. У цьому випадку легко визначит: що використовується шифр саме перестановки — досить пересвідчитись, що кожна буква зустрічається в повідомленні та криптотексті з однаковою частотою.
ВПРАВИ
2.1. а) Зашифрувати слово cryptography за допомогою шифру заміни з ключем
abcdefghijklm nopqrstuvwxyz
badcfehgjilkn mporqtsvuxwzy
b) Дешифрувати криптотекст vmjufqtjsz, отриманий за використаня того ж ключа.
2.2. а) Довести, що послідовне застосування шифру простої заміни двічі, один раз з ключем К1, а другий раз з ключем К2, еквівалентне одноразовому застосуванню шифру заміни з деяким ключем К3.
b) Довести, що криптотекст, отриманий за допомогою шифру заміни з ключем К, можна дешифрувати, застосувавши шифр заміни з деяким ключем К'.
c) Нехай в позначеннях попереднього пункту К' = К, тобто дешифрування можна здійснити, застосувавши шифр з тим же ключем ще раз. Припустимо також, що при шифруванні з ключем К жоден символ алфавіту не залишається незмінним. Скільки ключів К для шифру заміни у 26-символьному
алфавіті мають такі дві властивості?
2.3. Для букви а у n-символьному алфавіті та цілого числа s, означимо їх суму а + s як результат циклічного зсуву букви а на s позицій у алфавіті, вправо якщо a > 0 і вліво інакше. Наприклад, для латинського алфавіту а + 3 = d, ь + (—3) = у. Довести співвідношення а) а + (s + п) = а + s; b) (а + s1) + s2 = а + (s1 + s2); с) (а + s1) + s2 = (а + s2) + s1 для будь-якої букви а та чисел s,s1,s2.
2.4. а) Довести, що послідовне застосування шифру зсуву двічі, одинраз з ключем s1, а другий раз з ключем s2, еквівалентне одноразовому застосуванню шифру зсуву з ключем s1 + s2;
b) Довести, що криптотекст, отриманий за допомогою шифру зсуву з ключем s, 0  s < п, можна дешифрувати, застосувавши шифр зсуву з ключем п — s.
s < п, можна дешифрувати, застосувавши шифр зсуву з ключем п — s.
2.5.Порахувати частоти всіх символів у тексті мама мила раму.
2.6.В потоці зашифрованих донесень від інформатора з Маріїнського палацу домінує буква н. Припустивши, що використовується шифр зсуву і пропуски між словами ігноруються, знайти за допомогою частотного аналізу ключ і розшифрувати повідомлення
опдрснкнмярстомзйнлопнвнкнчдмннкдкщйяспдсщнвн.
2.7. а) Використовуючи шифр чотирьох квадратів із пункту 2.3 з ключем як на малюнку 2, зашифрувати слово university.
ь) Дешифрувати криптотекст sknromra, отриманий за допомогою того ж шифру з тим же ключем.
2.8. а) Скільки різних k-грам є у n-символьному алфавіті?
ь) Скільки різних біграм є у алфавіті з 25 букв?
2.9. а) Скільки різних ключів має шифр чотирьох квадратів, описаний у пункті 2.3?
b) Вказати два різні ключі для шифру чотирьох квадратів, шифрування якими завжди дає однакові результати.
c) Скільки різних ключів має загальний біграмний шифр для 25-символьного алфавіту, який кожну біграму відкритого тексту переводить у біграму криптотексту в тому ж алфавіті?
d) Скільки з них можуть бути реалізовані як ключі для шифру чотирьох квадратів?
6 Єдиним винятком є слово иилискит — назва мінералу, запозичена з мови одного із малочисельних народів Півночі (примітка редактора).
2.10. а) Розглянувши операцію додавання букв алфавіту, введену в пунк ті 2.4, довести, що для будь-яких букв х, у, та z виконуються рівності (х + у) + z = х + (у + z) (асоціативність) та х + у = у + х (комутативність).
b) Позначимо через X та Y довільні два слова однакової довжини. До вести, що шифрування слова X за допомогою шифру Віженера з ключем У дасть той же результат, що й шифрування слова Y з ключем X.
2.11. а) Зашифрувати повідомлення білі мухи налетіли, використавши шифр Віженера з ключем зима.
b) Розшифрувати криптотекст ьччжпчьишисаєяйпявааьяч, отриманий за допомогою шифру Віженера з тим же ключем.
2.12.Показати, що шифр зсуву є частковим випадком шифру Віженера. Який ключ у шифрі Віженера над українським алфавітом слід взяти, щоб отримати шифр Цезаря?
2.13. а) Довести, що послідовне застосування шифру Віженера двічі, один раз з ключем К1 і другий раз з ключем К2 тої ж довжини, еквівалентне одноразовому застосуванню шифру з ключем К3, де К3 можна отримати шифруванням слова К1 з ключем К2.
b) Довести, що послідовне застосування шифру Віженера двічі, один раз з ключем K1 довжини l1 і другий раз з ключем К-2 довжини l2, еквівалентні одноразовому застосуванню шифру з деяким ключем К3 довжини l3, де l3з найменшим спільним кратним чисел l1та l2
2.14.Вибрати для шифру Віженера довільний ключ довжини а) 3, b) 6 і зашифрувати повідомлення бороніть королівну від ворогів. У отриманому криптотексті знайти однакові триграми або біграми і порахувати, на якій відстані одна від одної вони знаходяться.
2.15.(Ьeaufort) Для букви х алфавіту через — х позначимо протилєжну їй букву алфавіту, а саме таку, що сума номерів обох букв дорівнює кількості букв у алфавіті. Нагадаємо, що нумерація в алфавіті починається з 0. Покладемо також, що перша буква є протилежною сама до себе. При криптуванні за допомогою шифру Віженера кожна буква с криптотексту отримується із відповідних букв m і k повідомлення і ключа за формулою с — т + k, де операція додавання описана на стор. 23. Розглянемо модифікацію шифру при якій криптування здійснюється за формулою с = (—m) + k.
a)Зашифрувати повідомлення білі мухи налетіли за допомогою ключа зима.
b)Розшифрувати криптотекст етишфжвлчишізшюяюшен, отриманий за помогою того ж ключа.
с) Довести, що у якості алгоритму декриптування для цієї модифікації шифру Віженера можна взяти просто алгоритм криптування. Шифр з такою властивістю називається інволютивним.
2.16. а) Зашифрувати повідомлення білі мухи налетіли, за допомогою шифру з автоключем, взявши як ключ слово зима.
b) Розшифрувати криптотекст ьччжюбхошнпинтвпсккпікш, отриманий за допомогою того ж шифру з тим же ключем.
2.17.Зламати таку версію шифру з автоключем. Якщо ключ має довжину l, то відкритий текст розбивають на блоки довжини l кожен, які послідовно перетворюють у блоки криптотексту наступним чином. Перший блок криптотексту є сумою першого блоку відкритого тексту і ключа. Кожен наступний блок криптотексту отримують сумуванням відповідного блоку відкритого тексту із попереднім блоком криптотексту. (Не знаючи ключа, за криптотекстом можна відновити відкритий текст за винятком перших l літер.)
2.18 Довести, що послідовне застосування до досить довгого тексту двох блокових шифрів, одного з періодом l1 ,адругого з періодом l2, призводить до шифрування блоками довжини l, де l є найменшим спільним кратним чисел l1 i l2.
2.19. а) Зашифрувати за допомогою матричного шифру обходу з ключем, зображеним на малюнку 4, повідомлення you must strike while the iron is hot.
b) Дешифрувати криптотекст niuhngdsoneuahwtterndnne, отриманий з допомогою того ж шифру з тим же ключем.
2.20. а) Зашифрувати за допомогою шифру Кардано з ключем, зображеним на малюнку 5, слово недопереповнення.
b) Дешифрувати криптотекст ьетуркнеітсисвйи, отриманий тим же шифром з тим же ключем.
2.21.Виготовити ключ 6 на 6 для шифру Кардано і зашифрувати з його допомогою довільний текст із 36 букв.
2.22.Скільки є для шифру Кардано ключів розміру а) 4 на 4; b) 6 на 6; с) k на k, для парного k?
2.23. а) Зашифрувати за допомогою загального шифру перестановки з періодом 6 і ключем:

слово криптоаналіз.
b) Розшифрувати криптотекст оеекпреиолтп, отриманий з допомогою тoго ж шифру з тим же ключем.
2.24. Перехоплено три криптотексти: саннаа, бббаао і укаадк. Як стало відомо, перші два відповідають повідомленням ананас і баобаб. Розшифрувати третій криптотекст.
2.25. а) Довести, що послідовне застосування шифру перестановки двічі один раз з ключем К1 і другий раз з ключем К2 еквівалентне одноразовому застосуванню шифру з деяким ключем К3 (період фіксований).
b)Довести, що криптотекст, отриманий за допомогою шифру перестановки з ключем К, можна дешифрувати, застосувавши той же шифр з деяким ключем К’
c)Нехай у позначеннях попереднього пункту К’ = К, тобто дешифрування можна здійснити, застосувавши шифр з тим же ключем ще раз. Припустимо також, що при шифруванні з ключем К кожна буква переходить на нове місце. Скільки ключів К для шифру перестановки з періодом l маюті такі дві властивості?
2.26. а) Нехай А — шифр перестановки, а В — шифр заміни. Довести що застосування спочатку шифру А, а потім В, еквівалентне застосуванню спочатку шифру В, а потім А з тими ж ключами. (В такому випадку кажуть що шифри А і В комутують.)
b)Навести приклад двох шифрів перестановки, які не комутують.
c)Навести приклад двох шифрів заміни, які не комутують.
2.27 Довести, що послідовне застосування до досить довгого повідомлення двох шифрів перестановки з періодами l1 та l2, першого з ключем К а другого з ключем K’, еквівалентне одноразовому застосуванню шифру перестановки з деяким ключем K3 та періодом Із, що є найменшим спільним кратним чисел l2, l1
2.28.Використовується шифр перестановки з періодом 5. Визначити ключ і розшифрувати криптотекст
ничаз ніюон курте сюеіц терке ивйин рпбір иниви
нненк ьдубі зїокя зорга щинзи сьтєу рохоя мецно
ЛІТЕРАТУРА
Авторитетними джерелами з елементарної криптографії є [112] та [І43| Неперевершений у світовій літературі опис частотного аналізу належите Едгару По [49]. Поняття надлишковості мови введене в [60]. Шифр чотирьох квадратів у пункті 2.3 описано в [110]. Популярний виклад шифру Кардана міститься в [48, Розділ VI].
ЛЕКЦІЯ 4
Читайте також:
- IV. Вивчення нового матеріалу – 20 хв.
- IV. Вивчення нового матеріалу.
- IV. Вивчення нового матеріалу.
- IV. Подання нового матеріалу
- IІІ. Вивченняння нового навчального матеріалу.
- V. Вивчення нового матеріалу.
- V. Виклад нового матеріалу
- V. Закріплення нового матеріалу – 5хв.
- V. Пояснення нового матеріалу
- V.Пояснення нового матеріалу
- VII. Закріплення нового матеріалу і систематизація знань.
- Алгоритм розробки техніко-економічного обґрунтування будівництва нового та реконструкції діючих підприємств харчування.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Дві пропозиції XX століття |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |