• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Кінетика реакцій за нестаціонарною лінійною дифузією

Нестаціонарна дифузія спостерігається в неперемішуваних розчинах або твердих тілах. Можна виділити два випадки гетерогенних реакцій, коли поверхня розподілу фаз плоска або сферична. Швидкість реакції, яка контролюється нестаціонарною дифузією, визначається з розв¢язків рівнянь Фіка. Для того щоб розв¢язання було кількісне, необхідно задати початкові та граничні умови. Ці умови такі:

1) в початковий момент часу, коли реакція на поверхні ще не

почалася, концентрація речовини поблизу поверхні С_s дорі-

внює його концентрації С₀ у розчині:

t = 0 та С_s = С₀ (початкова умова);

2) якщо реакція на поверхні проходить дуже швидко (а це неодмінна умова реакцій, що проходять у дифузійній області), то у будь-який момент часу після початку процесу концентрація речовини біля поверхні практично дорівнює нулю:

t > 0 та С_s = 0 ( перша гранична умова);

3) крім того, при напівнескінченній дифузії концентрація речовини в глибині розчину повинна бути постійною:

t > 0, X = ¥ та С(X,t) = С₀ (друга гранична умова).

Для нестаціонарної лінійної напівнескінченної дифузії, коли речовина дифундує до плоскої поверхні, розв¢язок другого рівняння Фіка при цих початковій та граничній умовах має вигляд:

;

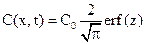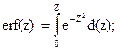(12.14)

,

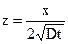де С(х, t) - концентрація речовини у даній точці на відстані x від поверхні твердого тіла у момент часу t; erf(z) - інтеграл помилок (відшукується за спеціальними таблицями за значенням z).

Підставляючи знайдене значення С(х,t) у перше рівняння Фіка, отримуємо рівняння для швидкості нестаціонарного гетерогенного процесу, який контролюється лінійною напівнескінченною дифузією (рівняння Коттреля):

(12.15)

При t ¥ W 0.

Для нестаціонарної сферичної нескінченної дифузії, коли реагуючою твердою поверхнею є сфера, розв¢язання рівнянь Фіка із заданими початковими та граничними умовами дадуть

(12.16)

де r - радіус сфери. В даному випадку після тривалого часу (t¥) швидкість гетерогенного процесу на сферичній поверхні падає до деякого постійного значення

W_{t ¥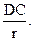} = (12.17)

Читайте також:

1. Визначення опорних реакцій трьохшарнірної арки
2. Визначення реакцій балки
3. Визначення реакцій в’язей
4. Викривлення реакцій горя
5. Елементи кінетики ланцюгових реакцій
6. Ембріологія ока. Вікові особливості зорових рефлекторних реакцій
7. ЕНЕРГЕТИКА І КІНЕТИКА РЕАКЦІЙ.
8. Закон діючих мас. Константи рівноваги гомогенних реакцій
9. Замикання тимчасових зв’язків. Нейронні кореляти формування і прояву умовно-рефлекторних реакцій.
10. Кінетика гетерогенних реакцій за стаціонарною лінійною дифузією
11. Кінетика екстракції
12. Кінетика зворотних реакцій першого порядку

Переглядів: 541