• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рівняння Клапейрона-Клаузіуса

Рівняння Клапейрона-Клаузіуса відображає особливості фазових переходів першого роду. Виведемо це рівняння, розглядаючи систему, у якій при постійних тиску та температурі у рівновазі перебувають рідина та її пара. Якщо випарити рівноважним чином визначену кількість (наприклад, 1 моль) рідини, то змінення внутрішньої енергії буде дорівнювати

DU = TDS - PDV або

U_п - U_р = T(S_п -S_р ) – P(V_п - V_р ).

Звідси

U_п + PV_п - TS_п = U_р + PV_р - TS_р

і

G_п = G_р. (6.2)

Якщо змінити температуру та тиск системи, то мольні енергії Гіббса теж зміняться і будуть дорівнювати

G_п + dG_п i G_р + dG_р .

Змінення Р і Т проведемо так, щоб система у новому стані знов перебувала у рівновазі. Тоді

G_п + dG_п = G_р + dG_р ,

dG_п = dG_р . (6.3)

Тобто, щоб при зміненні температури та тиску рівновага не змінилася, змінювання мольної енергії Гіббса (хімічного потенціалу) пари повинно дорівнювати її зміненню для рідини.

Використовуючи вираз для диференціала енергії Гіббса, отримуємо

-S_пdT + V_пdP = -S_рdT + V_рdP,

або

(V_п – V_р)dP = (S_п – S_р)dT. (6.4)

Ураховуючи, що випарювання проводиться при постійній температурі, приріст ентропії при переході рідини у пару можна виразити через приховану теплоту випарювання (DH_в)

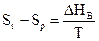. (6.5)

Беручи до уваги отримане співвідношення, отримуємо

DН_в = T(V_п –V_р). (6.6)

Це рівняння Крапейрона-Клаузіуса у диференціальному вигляді. Його можна записати і для інших фазових переходів. Так, для возгонки (сублімації)

DН_С = T(V_п –V_т ) . (6.7)

Для плавлення

DН_пл = T(V_р –V_т ) . (6.8)

У загальному випадку будь-якого фазового переходу

DН_ф = T(V₂ –V₁ ) . (6.9)

Рівняння Клапейрона-Клаузіуса подає залежність тиску пари над рідиною або твердим тілом (рівновага рідина-пара або тверде тіло –пара) від температури або залежність температури плавлення (рівновага тверде тіло – рідина) від тиску. Ці залежності, як правило, подають у вигляді діаграм стану. У наступних розділах при розгляданні діаграм стану ми будемо використовувати виведені співвідношення.

Для фазових переходів з участю пари (випарювання, сублімація, конденсація) отримане рівняння Клапейрона-Клаузіуса можна перетворити у більш зручне для практичного використання рівняння. Для цього необхідно зробити такі припущення:

1 Пар мати за ідеальний газ, для одного моля якого

PV = RT;

2 Знехтувати мольним об¢ємом рідкої або твердої речовини порівняно до мольного об¢єму пари;

3 Знехтувати залежністю теплоти фазового переходу від температури (це справедливо для невеликих інтервалів температур).

Тоді для процесу випарювання, наприклад, можна

записати

DН_в = T×V_п . (6.10)

Але V_п = RT/P і звідси

,

aбо

. (6.11)

Інтегруючи цей вираз у межах від Р₁ до Р₂ і відповідно від Т₁ до Т₂ , отримуємо

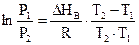. (6.12)

При інтегруванні співвідношення (6.11) у вузькому довільному інтервалі температур отримуємо

. (6.13)

Тут В – стала інтегрування. Для процесу сублімації

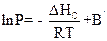(6.14)

Рівняння (6.13) і (6.14) показують, що логарифм тиску пари над твердою і рідкою речовиною лінійно залежить від зворотної температури (рис.6.1). Нахил цих прямих залежить від величини теплоти фазового переходу. Оскільки DН_С > DН_в, пряма для твердої речовини є більш крутою, ніж пряма для рідини. Точка перетину цих прямих відповідає температурі плавлення речовини.

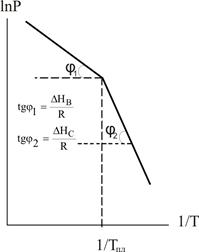
Рисунок 6.1 – Залежність lnP = f(1/T)

Виведені нами залежності lnP = f(1/T) мають велике практичне значення. За допомогою таких рівнянь розраховують значення тиску насиченої пари над рідкою та твердою речовинами при різних температурах. Справа у тому, що у довідниках з фізичної хімії є багато даних що до тисків насичених парів у вигляді коефіцієнтів рівняння:

ln P = B – A/T. (6.15)

Тут А = DН/R, а Р – тиск насиченої пари, що поданий у мм ртутного стовпа. При цьому зазначається температурний інтервал, у якому виконується ця залежність. І якщо необхідно знати тиск насиченої пари над будь-якою речовиною, зовсім необов¢язково виміряти цей тиск експериментально, а слід лише знайти коефіцієнти А і В у довіднику. Наприклад, тиск насиченої пари над твердим ZnCl₄ відшукують за допомогою рівняння

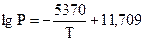(503-673 K).

Звідки DН_С (ZnCl₄) = 102,7 кДж/моль.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Асимптотичний підхід до порівняння оцінок
3. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
4. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
5. Вивід основного рівняння фільтрації
6. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
7. Головне рівняння відцентрового насоса. Теоретичний напір.
8. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.
9. Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
10. Динамічна інтерпретація диференційного рівняння другого порядку. Консервативні системи.
11. Диференціальне рівняння
12. Диференціальне рівняння Ейлера для потоку рідини.

Переглядів: 3026