Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Лекція 1 Вступ. Поняття про теорію ймовірностей. Зміст і завдання предмету. Основні поняття теорії ймовірностей. Класичне, статистичне та геометричне означення ймовірності

Для винесення будівлі в натуру необхідні горизонтальна і вертикальна прив'язки. Горизонтальна прив'язка здійснюється на головному кресленні генерального плану "Розбивочного плану (план розташування будівель і споруд)" шляхом прив'язки координаційних осей будівлі до опорних точок топографічного плану.

Суть вертикальної прив'язки полягає в закріпленні на місцевості відмітки чистої підлоги першого поверху, відповідній відмітці ±0,000 на робочих кресленнях будівлі, а також в нанесенні відміток землі по кутах будівлі, при входах і інших характерних точках. За наявності цих відміток стає можливим точно закласти фундаменти на встановлену проектом глибину, правильно визначити положення зовнішніх входів, конструктивне вирішення сходів, цоколів, рамп, підземних комунікацій та ін.

Прив'язку чистої підлоги здійснюють шляхом вказівки цієї відмітки на плані будівлі в системі генерального плану. У практиці проектування призначення цієї відмітки залежить від багатьох чинників. Однією з важливих умов будівництва є розташування горизонтальної гідроізоляції в стінах і пов'язаним з нею рівнем підлоги першого поверху вище за поверхню землі. Найменша відстань від рівня гідроізоляції до землі за умовами захисту від замочування атмосферними опадами, - приблизно 20см. Цей розмір призначають в найбільш високій точці рельєфу; з падінням рельєфу відстань до землі збільшуватиметься по довжині будівлі. Положення землі у входів в будинки визначатиме вирішення вхідних сходів, кількість сходинок, що зв'язують поверхню землі з рівнем першого поверху. Ці сходинки можуть складати цокольний марш сходової клітки або бути зовнішніми у складі вхідного крильця (рис. 8, 9).

По планувальному рішенню секції можуть бути двох типів.

1 тип. – сходова клітка розташована напроти входу в секцію (рис. 8).

2 тип. – сходова клітка розташована біля входу в секцію (рис. 9).

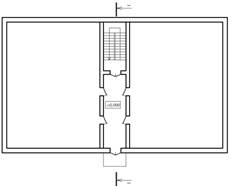
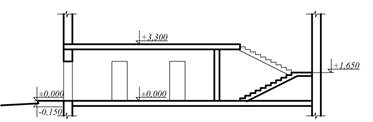Рис. 8. Перший тип секції.

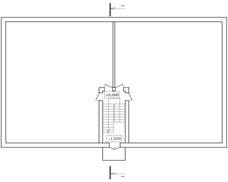
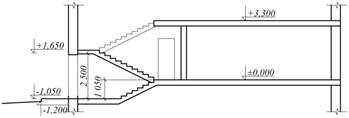Рис. 9. Другий тип секції.

При великому перепаді рельєфу по відношенню до найвищої точки будівлі (секції) і входу, виникає велика кількість сходинок. У такому разі необхідно застосувати другий тип секції, тобто частина рівнів (7шт.) розміщуються усередині секції (рис.9).

У розрахунково-графічній роботі необхідно підрахувати необхідну кількість сходинок біля зовнішнього входу.

При значному падінні рельєфу і збільшенні висоти цокольного поверху доцільно окремі секції будівлі розташовувати на різних рівнях з перепадами на половину поверху, але не менше 1,5 - 2,0 метра і позначати відмітки підлоги перших поверхів в кожній секції.

По периметру будівель владнують відмостку з умовною шириною в 1м. Відмітки землі по кутах будівель і при вході вказують по зовнішній грані відмостки у вигляді дробу: у чисельнику - проектна відмітка, яка обчислюється по проектних горизонталях, в знаменнику – фактична відмітка. Проектні горизонталі доводять лише до зовнішньої грані відмостки, на самій відмостці проектні горизонталі не показують. За відсутності або при поєднанні відмосток з тротуаром горизонталі доводять до стін будівлі, при цьому поперечний ухил смуги тротуару шириною 1,0м, що примикає до стіни, має бути не менше 0,03.

Додаток 1

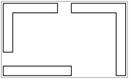
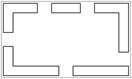
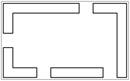
Варіанти завдань

Остання цифра залікової книжки	Передостання цифра залікової книжки
№№	Схема	№№	Ухил⁰/₀₀	№№	Ухил⁰/₀₀

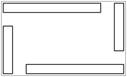
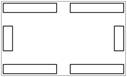
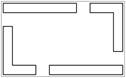
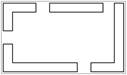
Додаток 2

Приклад побудови підготовчого креслення в розмірах

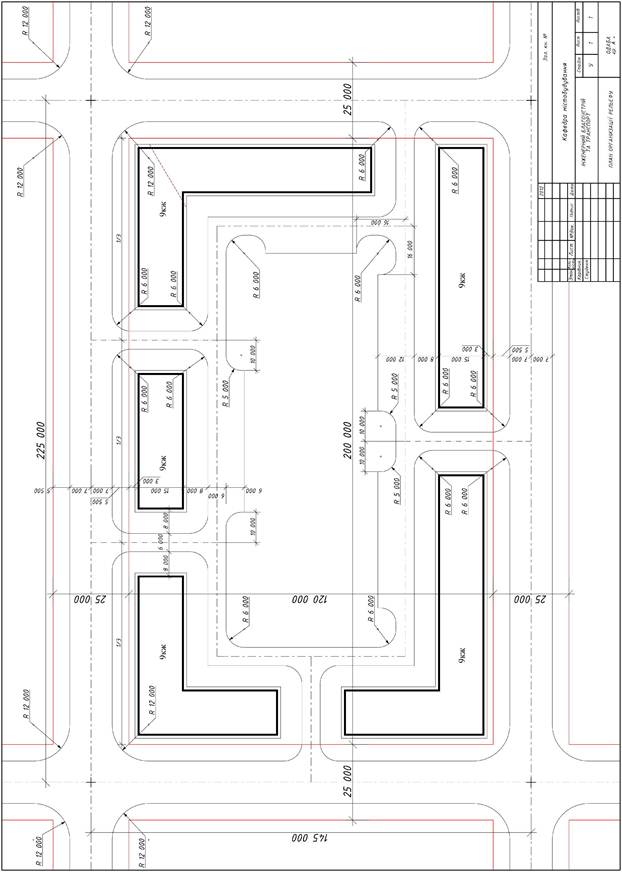
Додаток 3

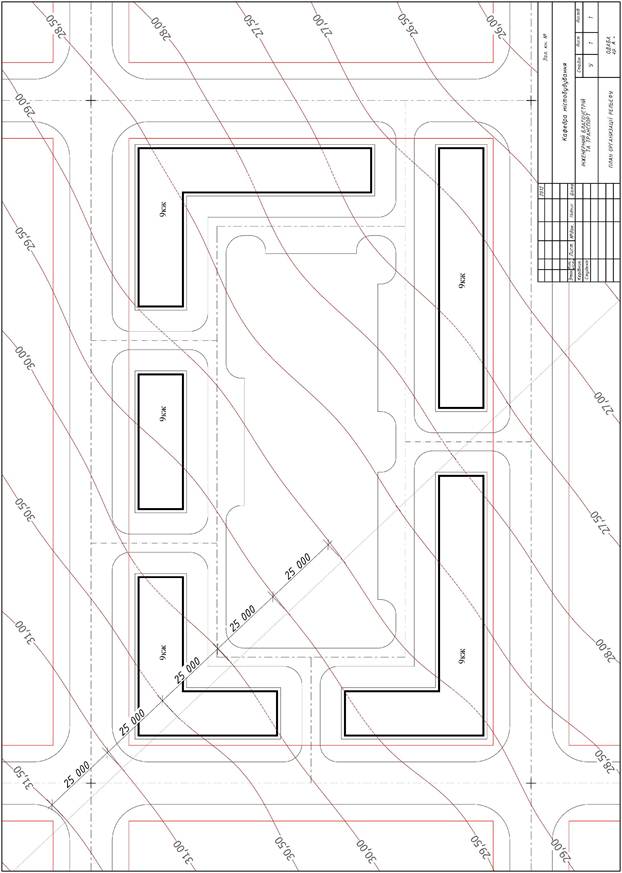Приклад побудови креслення з заданим ухилом рельєфу

Додаток 4

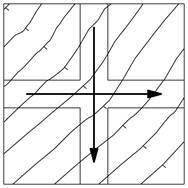
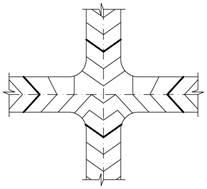
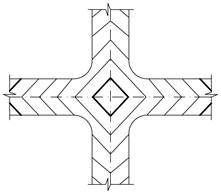
Прийоми вертикального планування простих перехресть

а) на узгір'ї

б) на тальвезі

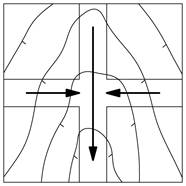
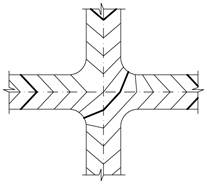
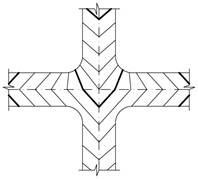
в) на вододілі

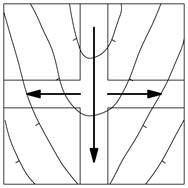
г) на горбі

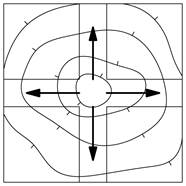
Додаток 5

Приклад оформлення роботи

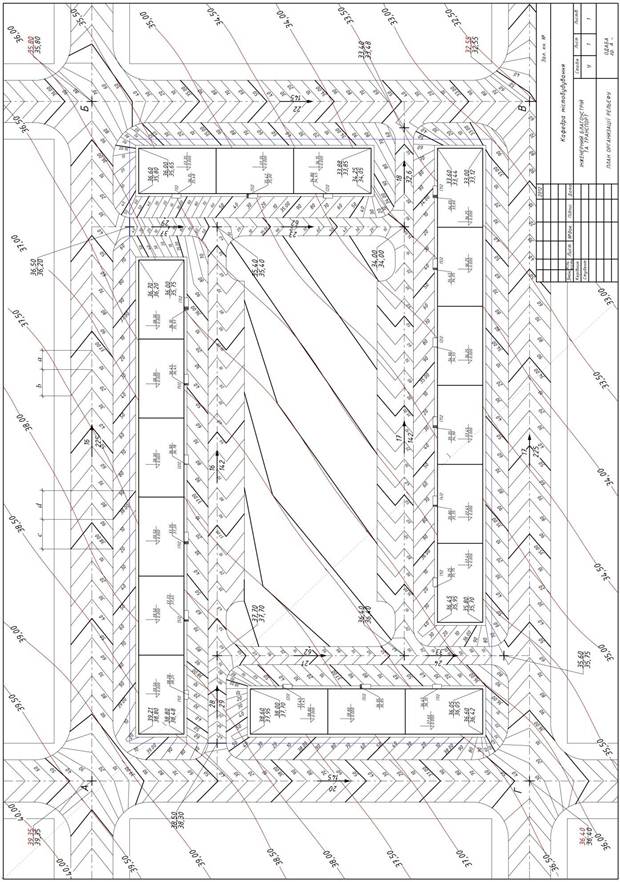
Додаток 6

Приклад планування території

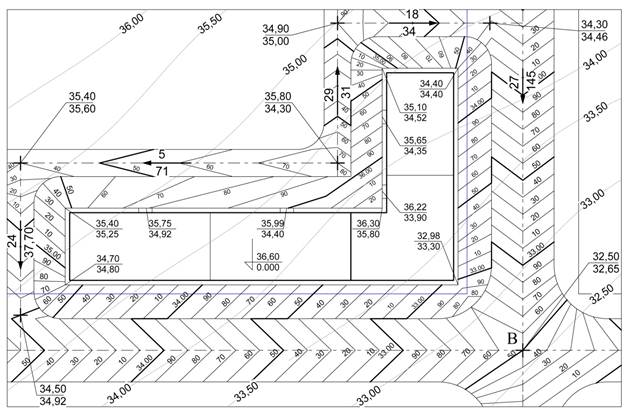
Додаток 7

Приклад оформлення штампу

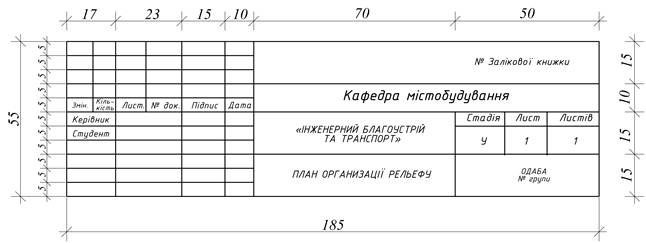
Додаток 8

Умовні позначення

Умовне позначення

Опис

Уклон, ⁰/₀₀ Уклонопоказчик Відстань між переломними точками

Точка перелому (зміни рельєфу)

31,25 31,15

Проектна відмітка (червона) Фактична відмітка (чорна)

Фактичні горизонталі

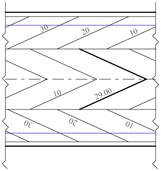
Проектні (червоні) горизонталі

ЛІТЕРАТУРА

1. ГОСТ 21.508-93. Правила выполнения рабочей документации генеральных планов предприятий, сооружений и жилищно-гражданских объектов.

2. ДБН 360-92** Планировка и застройка городских и сельских поселений.

3. ДБН В.2.3-5-2001. Улицы и дороги населенных пунктов.

4. Евтушенко М.Г. Инженерная подготовка территорий населенных мест. М.Г. Евтушенко, Л. В. Гуревич, В. Л. Шафран - М.: Стройиздат, 1982.

5. Каплан Л.З. Инженерная подготовка территорий строительства - М.: Госстройиздат, 1961.

6. Линник І.Е. Інженерна підготовка територій населених місць: Навчальний посібник.- Харків: ХДАМГ, 2003.- 337с.

7. Методические указания к выполнению курсовой работы по дисциплине «Инженерное благоустройство и транспорт» на тему «План организации рельефа» (вертикальная планировка) для студентов базового направления 1201-АРХИТЕКТУРА. Одесса, ОГАСА-2005

8. Черепанов В.А. Инженерное проектирование планировки городов. (транспорт и благоустройство территорий). В.А. Черепанов, Л.В. Гуревич, М.Г. Евтушенко – М.: Стройиздат, 1971.

Лекція 1 Вступ. Поняття про теорію ймовірностей. Зміст і завдання предмету. Основні поняття теорії ймовірностей. Класичне, статистичне та геометричне означення ймовірності

Події в навколишньому світі можна поділити на вірогідні, неможливі та випадкові. Перші при реалізації певного комплексу умов (при випробуванні) відбуваються завжди, другі –ніколи, треті – можуть як відбуватися, так і не відбуватися. Віднесення певної події до тієї або іншої групи істотно залежить від умов випробування. Наприклад, розглянемо подію, зв’язану з попаданням у мішень. Для цього треба, щоб хтось стріляв, щоб була мішень, щоб був засіб реалізації попадання , щоб цей засіб був доступний (справжній), щоб була забезпечена певна відстань до мішені і т.д. Якщо якась з умов не виконана, то подія буде неможливою; якщо будуть виконані всі необхідні і достатні умови, то подія буде достовірною (скажімо пістолет упирається в мішень).

Основним тут є поняття випробування. Під випробуванням розуміємо забезпечення всіх необхідних умов для появи даної події. Події позначають літерами латинської абетки А, В, С, ....

Випадкові події займають проміжну позицію між “ завжди” і “ ніколи”. І можуть наставати чи не наставати в даному випробуванні, в якому виконані всі необхідні умови появи їх. Стосовно достатніх умов зазначимо, що вони не завжди підконтрольні, а про деякі з них важко здогадатися. Так, ми не контролюємо пориву вітру чи спалаху блискавки, які могли спричинити наш промах по мішені. У такій ситуації не можна обмежитися одиничними випробуваннями, а треба мати якомога більшу їх кількість і аналізувати всю множину отриманих результатів. Ця множина є більш стійкою, оскільки одна частина попадань відхиляється в один бік, а друга в другий, і ці випадкові відхилення взаємно компенсуються, відкриваючи шлях до закономірності.

Ось чому теорія ймовірності як наука про числову міру випадковості подій передбачає вивчення не одиничних, а масових однорідних випадкових подій, які підпорядковуються стохастичним ( від грець. “стохастіс” – здогадка ) закономірностям, встановлення яких і є її основною задачею.

Виникнення теорії ймовірностей , обумовлене спробою побудувати теорію азартних ігор, відноситься до ХVІ-ХVІІ ст.. і зв’язане з іменами таких учених, як Дж. Кардано, Б. Паскаль, Х. Гюйгенс, П. Ферма. Найістотнішим досягненням її першого періоду є відкриття Д. Бернуллі закону великих чисел. Другий період розвитку теорії ймовірностей зв’язаний з іменами Лапласа, Пуассона, К. Гаусса, Буняковського ( ХVІІ-ХІХ ст.). Як наука теорія ймовірностей сформувалась на межі ХІХ – ХХ ст.. завдяки зусиллям П.Л.Чебишева, О.М.Ляпунова, О.О.Маркова, Р. Мізеса. Проте в 30-х роках нашого століття вона стала повноцінним розділом математики ( до цього вважалась прикладною дисципліною) завдяки чіткому поняттю ймовірності, даному .М.Колмогоровим.

Подамо кілька означень.

Випадкові події поділяються на сумісні й несумісні . У першому випадку поява однієї події не виключає, а в другому виключає появу другої події. Наприклад, осічка і непопадання в ціль – сумісні, осічка і попадання в ціль – несумісні події.

Кілька подій утворюють повну групу, якщо поява хоч однієї з них – вірогідна подія. Наприклад, поява аверса і реверса при киданні монети, поява числа очок від одиниці до шести при киданні гральної кості, попадання і промах.

Кілька подій називають рівноможливими, якщо при випробуванні вони з’являються однаково часто. Так, аверс і реверс- рівноможливі, але попадання і промах, як правило, - ні.

Деякі події наступають досить часто, а деякі – навпаки, дуже рідко. Введемо числову характеристику показника настання події.

ОзначенняЙмовірністю Рданої події А називається відношення числа результатів випробувань m, які сприяють появі даної події, до загального числа n рівноможливих і єдино можливих результатів випробувань, які утворюють повну групу, тобто

Р (А) = m / n (1.1)

Наведене означення називається класичним.

З означення випливають властивості ймовірності: для вірогідних подій Р = 1

( m = n ), для неможливих Р = 0 ( m = 0), для випадкових 0 < P < 1 (0 < m < n).

Приклад

У групі з 25 студентів п’ять дівчат. Знайти ймовірність того, що з цієї групи першою до аудиторії зайде дівчина.

Розв’язування. Маємо Р (А) = 5 / 25 = 0,2

Приклад

Знайти ймовірність того , що при киданні гральної кості випаде грань з парною кількістю очок .

Розв’язування. Маємо n = 6, m = 3. Отже, Р (А) = 0,5.

Класичне означення ймовірності, з одного боку, просте, наочне, конструктивне, а з другого боку, воно має ряд суттєвих недоліків, а саме: не завжди можна подати результат випробувань як сукупність рівно можливих результатів; m і n скінченні, але це не завжди так; рівноможливість і рівноймовірність –синоніми. Отже , формула (1.1) не є коректним означенням. Геометричне означення ймовірності з’явилося завдяки спробі відмовитися від скінченності величин m і n. Воно полягає в тому, що

де mes g і mes G - міри ( довжини, площі, об’єми) простору всіх (G) результатів і сприятливих (g) результатів.

Приклад

Два студенти домовилися зустрітися в певному місці між 15-ю та

16-ю год. Перший, хто прийде, чекає на другого не більше 20 хв. Яка ймовірність їхньої зустрічі?

Розв’язування. Нехай х – час приходу першого, а у – другого студента. Тоді mes G = 1 - площа квадрата зі стороною, яка дорівнює одиниці (рис. 1). Умова зустрічі має вигляд ½у - х½£ , тобто 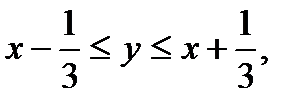звідки маємо

mes g = 5/9. Отже, Р (А) = 5 / 9.

у 16

15 16 x

Рисунок 1

Наведемо статистичне означення ймовірності: основним поняттям тут є відносна частота появи подій в результаті проведених випробувань

де n – число проведених випробувань, а m – число випробувань, в яких відбувалася подія А.

Ймовірність – це теоретична величина, обчислена до чи без проведення випробувань, відносна частота – величина емпірична, обчислена за результатами випробувань.

Визначення величини W (А) для різних подій показало, що в одних випадках вона для різних серій випробувань змінюється мало, а в других – істотно.

Якщо W (A) ≈ C, то подію А називають статистично стійкою, в решті випадків – нестійкою. У подальшому останні ситуації не розглядатимемо (це, як правило, ситуації, обумовлені “людським фактором”).

Переважна більшість помилок, зв’язаних із застосуванням теорії ймовірностей, пояснюється її спробами аналізувати невизначені події, які дістаємо у випробуваннях з великим числом неконтрольованих умов (про яку ймовірність виграшу команди можна вести мову, якщо тренери заздалегідь домовилися про нічию). Через це в означенні випадкової події обов’язково слід передбачити її статистичну стійкість.

ОзначенняСтатистичною ймовірністю події А називається число, навколо якого групуються відносні частоти цієї події або сама частота.

Р.Мізес встановив, що для випадкових подій

(для невизначених подій така границя не існує).

У 1900 р. відбувся Другий всесвітній математичний конгрес, на якому Д.Гільберт висунув 23 найважливіші проблеми. Шоста проблема Гільберта – побудова логічних несуперечливих основ теорії ймовірностей. Цю проблему було розв’язано через 33 роки О.Колмогоровим, який запропонував таку систему аксіом, яка дає означення ймовірностей:

1) кожній випадковій події А відповідає невід’ємне число Р (А), яке називається ймовірністю цієї події,

2) для вірогідної події U Р (U)=1,

3) ймовірність появи хоча б однієї з попарно несумісних подій дорівнює

сумі ймовірностей цих подій.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Словник	\|	Домашнє завдання

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.01 сек.