
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Завдання 3.
3а). Ступінь варіації ознаки визначається за значенням коефіцієнта варіації Vs відповідно до оцінної шкали варіації ознаки:
0% < Vs 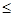 40%- варіація незначна;
40%- варіація незначна;
40% < Vs 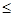 60%- варіація середня (помірна);
60%- варіація середня (помірна);
Vs > 60% - варіація значна.
Висновок:
Для ознаки вартість активів показник Vs= 92,06. Оскільки значення показника лежить у діапазоні Vs > 60% оцінної шкали, то, варіація - значна.
Для ознаки фінансовий результат показник Vs= 189,58. Оскільки значення показника лежить у діапазоні Vs > 60% оцінної шкали, то, варіація - значна.
3б). Ступінь однорідності сукупності за ознакою, що вивчається, для нормального і близьких до нормального розподілів встановлюється за значенням коефіцієнта варіації Vs.Якщо V 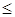 33%, то за даною ознакою розбіжності між значеннями ознаки невеликі. Якщо при цьому одиниці спостереження відносяться до одного певного типу, то сукупність, що вивчається, однорідна.
33%, то за даною ознакою розбіжності між значеннями ознаки невеликі. Якщо при цьому одиниці спостереження відносяться до одного певного типу, то сукупність, що вивчається, однорідна.
Висновок:
Для ознаки вартість активів показник  отже, за даною ознакою вибіркова сукупність неоднорідна.
отже, за даною ознакою вибіркова сукупність неоднорідна.
Для ознаки фінансовий результат показник  отже, за даною ознакою вибіркова сукупність неоднорідна.
отже, за даною ознакою вибіркова сукупність неоднорідна.
3в). Для оцінки кількості попадань індивідуальних значень ознаки xi у той або інший діапазон відхилення від середньої 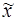 , а також для виявлення структури розсіювання значень xi після 3-го діапазону формується табл. 1.9 (з конкретними числовими значеннями меж діапазонів).
, а також для виявлення структури розсіювання значень xi після 3-го діапазону формується табл. 1.9 (з конкретними числовими значеннями меж діапазонів).
Таблиця 1.9
Розподіл значень ознаки по діапазонах розсіяння ознаки відносно 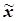
| Межі діапазонів, млн. грн. | Кількість значень xi, що знаходяться в діапазоні | Процентне співвідношення розсіювання значень xi за діапазонами, % | ||||
| Перша ознака | Друга ознака | Перша ознака | Друга ознака | Перша ознака | Друга ознака | |
| А | ||||||
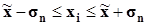
| [1001,35; 24215,77] | [-70,44; 227,76] | ||||
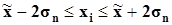
| [-10605,86; 35822,98] | [-219,54; 376,86] | ||||

| [-22213,07; 47430,19] | [-368,64; 525,96] |
На основі даних табл. 1.9 структура розсіювання значень ознаки за трьома діапазонами (колонки 5 і 6) зіставляється із структурою розсіювання за правилом «трьох сигм», справедливим для нормальних і близьких до нього розподілів:
68,3% значень розташовуються в діапазоні ( 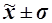 ),
),
95,4% значень розташовуються в діапазоні (  ),
),
99,7% значень розташовуються в діапазоні (  ).
).
Якщо отримана в таблиці 1.9 структура розсіювання хi після 3-го діапазону трохи розходиться з правилом «трьох сигм», можна припустити, що розподіл одиниць сукупності за даною ознакою близький до нормального.
Розбіжність з правилом «трьох сигм» може бути істотною. Наприклад, менше 60% значень хi потрапляють у центральний діапазон ( 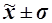 ) або більше 5% значень хi виходить за діапазон (
) або більше 5% значень хi виходить за діапазон (  ). У цих випадках розподіл не можна вважати за близький до нормального.
). У цих випадках розподіл не можна вважати за близький до нормального.
Висновок:
Порівняння даних колонки 5 табл. 1.9 за правилом «трьох сигм» показує на їх істотну розбіжність, отже, розподіл одиниць сукупності за ознакою вартість активів не можна вважати близьким до нормального.
Порівняння даних колонки 6 табл. 1.9 за правилом «трьох сигм» показує на істотну розбіжність, отже, розподіл одиниць сукупності за ознакою фінансовий результат не можна вважати близьким до нормального.
Завдання 4. Для відповіді на питання 4а) – 4в) необхідно скористатися табл.1.8 і порівняти величини показників для двох ознак.
Для порівняння ступеня варіації значень ознак, що вивчаються, ступеня однорідності сукупності за цими ознаками, надійності їх середніх значень використовуються коефіцієнти варіації Vs ознак.
Висновок:
Оскільки Vs для першої ознаки менше, ніж Vs для другої ознаки, то варіація значень першої ознаки менше варіації значень другої ознаки, сукупність більш однорідна за першою ознакою, середнє значення першої ознаки є більш надійнішим, ніж у другої ознаки.
Завдання 5. Інтервальний варіаційний ряд розподілу одиниць сукупності за ознакою вартість активів представлений у табл. 1.7, а його гістограма і кумулята – на рис. 1.2.
Можливість віднесення розподілу ознаки «вартість активів» до нормального розподілу встановлюється шляхом аналізу форми гістограми розподілу. Аналізується кількість вершин в гістограмі, її асиметричність і вираженість «хвостів», тобто частоти появи в розподілі значень, що виходять за діапазон (  ).
).
1. При аналізі форми гістограми, перш за все, слід оцінити розподіл варіантів ознаки за інтервалами (групами). Якщо на гістограмі чітко простежуються два-три «горби» частот варіантів, це говорить про те, що значення ознаки концентруються відразу в декількох інтервалах, що не відповідає нормальному закону розподілу.
Якщо гістограма має одновершинну форму, є підстави припускати, що вибіркова сукупність може мати характер розподілу, близький до нормального.
2. Для подальшого аналізу форми розподілу використовуються описові параметри вибірки – показники центру розподілу ( 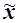 , Мо, Me) і варіації (
, Мо, Me) і варіації ( 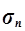 ). Сукупність цих показників дозволяє дати якісну оцінку близькості емпіричних даних до нормальної форми розподілу.
). Сукупність цих показників дозволяє дати якісну оцінку близькості емпіричних даних до нормальної форми розподілу.
Нормальний розподіл є симетричним, і для нього виконуються співвідношення:
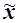 =Mo=Me
=Mo=Me
Порушення цих співвідношень свідчить про наявність асиметрії розподілу. Розподіли з невеликою або помірною асиметрією в більшості випадків відносяться до нормального типу.
3. Для аналізу довжини «хвостів» розподілу використовується правило «трьох сигм». Згідно цього правила в нормальному і близьким до нього розподілах крайні значення ознаки (близькі до хmin і хmax) зустрічаються багато рідше (5-7 % всіх випадків), ніж, ті, що знаходяться в діапазоні (  ). Отже, за відсотком виходу значень ознаки за межі діапазону (
). Отже, за відсотком виходу значень ознаки за межі діапазону (  ) можна судити про відповідність довжини «хвостів» розподілу нормальному закону.
) можна судити про відповідність довжини «хвостів» розподілу нормальному закону.
Висновок:
1.Гістограма є одновершинною.
2. Розподіл істотно асиметричний, оскільки параметри 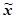 , Мо, Me відрізняються значно:
, Мо, Me відрізняються значно:
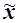 = 12608,56, Mo = 7571,7, Me = 4790,65.
= 12608,56, Mo = 7571,7, Me = 4790,65.
3. “Хвости” розподілу не дуже довгі, оскільки згідно колонки 5 табл. 1.9 7% варіантів лежать за межами інтервалу (  )=([-10605,86; 35822,98) млн. грн.
)=([-10605,86; 35822,98) млн. грн.
Отже, на підставі п.п. 1,2,3, не можна зробити висновок про близькість розподілу, що вивчається, до нормального.
II. Статистичний аналіз генеральної сукупності
Завдання 1. Розраховані в табл. 1.3 генеральні показники представлені в табл. 1.10.
Таблиця 1.10
Описові статистики генеральної сукупності
| Узагальнюючі статистичні показники сукупності за ознаками, що вивчаються | Ознаки | |
| вартість активів | фінансовий результат | |
Стандартне відхилення  , млн. грн. , млн. грн.
| 11820,21 | 151,85 |
Дисперсія 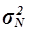
| 139717323,49 | 23059,29 |
| Асиметричність As | 1,14 | 2,028 |
| Ексцес Ek | 0,12 | 3,34 |
Для нормального розподілу справедлива рівність
RN=6Ns.
В умовах близькості розподілу одиниць генеральної сукупності до нормального це співвідношення використовується для прогнозної оцінки розмаху варіації ознаки в генеральній сукупності.
Очікуваний розмах варіації ознак RN:
- для першої ознаки RN= 38100,73,
- для другої ознаки RN = 613,38.
Співвідношення між генеральною і вибірковою дисперсіями:
- для першої ознаки 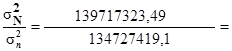 1,04,тобто розбіжність між дисперсіями незначна;
1,04,тобто розбіжність між дисперсіями незначна;
-длядругої ознаки  1,04,тобто розбіжність між дисперсіями незначна.
1,04,тобто розбіжність між дисперсіями незначна.
Завдання2. Застосування вибіркового методу спостереження пов'язане з вимірюванням міри достовірності статистичних характеристик генеральної сукупності, отриманих за наслідками вибіркового спостереження. Достовірність генеральних параметрів залежить від репрезентативності вибірки, тобто від того, наскільки повно і адекватно представлені у вибірці статистичні властивості генеральної сукупності.
Як правило, статистичні характеристики вибіркової і генеральної сукупностей не збігаються, а відхиляються на деяку величину е, яку називають похибкою вибірки(похибкою репрезентативності). Похибка вибірки – це різниця між значенням показника, який був отриманий за вибіркою, і генеральним значенням цього показника. Наприклад, різниця
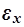 = |
= | 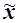 -
-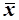 |
|
визначає похибку репрезентативності для середньої величини ознаки.
Оскільки похибки вибірки завжди випадкові, обчислюють середню і граничну похибки вибірки.
1. Для середнього значення ознаки середня похибка вибірки 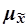 (її називають також стандартною помилкою) виражає середнє квадратичне відхилення sвибіркової середньої
(її називають також стандартною помилкою) виражає середнє квадратичне відхилення sвибіркової середньої 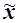 від математичного очікування M[
від математичного очікування M[ 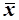 ] генеральної середньої
] генеральної середньої 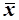 .
.
Для ознак, що вивчаються, середні похибки вибірки 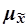 наведені в таблиці 3:
наведені в таблиці 3:
- для ознаки вартість активів
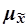 = 2233,81,
= 2233,81,
- для ознаки фінансовий результат
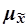 = 28,7.
= 28,7.
2. Гранична похибка вибірки  визначає межі, в межах яких лежить генеральна середня
визначає межі, в межах яких лежить генеральна середня 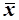 . Ці межі задають так званий довірчий інтервал генеральної середньої
. Ці межі задають так званий довірчий інтервал генеральної середньої 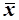 – випадкову область значень, яка з ймовірністю P, близькою до 1, гарантовано містить значення генеральної середньої. Цю ймовірність називають довірчою ймовірністю або рівнем надійності.
– випадкову область значень, яка з ймовірністю P, близькою до 1, гарантовано містить значення генеральної середньої. Цю ймовірність називають довірчою ймовірністю або рівнем надійності.
Для рівнів надійності P=0,954; P=0,683оцінки граничних похибок вибірки  подано в таблицях 1.3 і 1.4.
подано в таблицях 1.3 і 1.4.
Для генеральної середньої граничні значення і довірчі інтервали визначаються виразами:
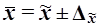 ,
,

Граничні похибки вибірки і очікувані межі для генеральних середніх подані в таблиці 11.
Таблиця 1. 11
Граничні похибки вибірки і очікувані межі для генеральних середніх
| Ймовірність Р | Коефі-цієнт довіри t | Граничні похибки вибірки, млн. грн. | Очікувані межі для середніх, млн. грн. | ||
| для першої ознаки | для другої ознаки | для першої ознаки | для другої ознаки | ||
| 0,683 | 2233,81 | 28,7 | 10374,75 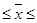 14842,37 14842,37
| 49,96 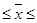 107,36 107,36
| |
| 0,954 | 4467,62 | 57,4 | 8140,94 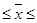 17076,18 17076,18
| 21,26 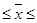 136,06 136,06
|
Висновок:
Збільшення рівня надійності веде до розширення очікуваних меж для генеральних середніх.
Завдання 3.Розраховані в табл. 1.3 значення коефіцієнтів асиметрії Asі ексцесу Ekдані в табл. 1.10.
1.Показник асиметрії As оцінює зміщення ряду розподілу вліво або вправо по відношенню до осі симетрії нормального розподілу.
Якщо асиметрія правостороння (As>0)те права частина емпіричної кривої виявляється довше лівої, тобто має місце нерівність 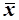 >Me>Mo,що означає переважну появу в розподілі вищих значень ознаки (середнє значення
>Me>Mo,що означає переважну появу в розподілі вищих значень ознаки (середнє значення 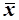 більше серединного Meі модального Мо).
більше серединного Meі модального Мо).
Якщо асиметрія лівостороння (As<0), то ліва частина емпіричної кривої виявляється довше правої і виконується нерівність 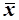 <Me<Mo,що означає, що в розподілі частіше зустрічаються нижчі значення ознаки (середнє значення
<Me<Mo,що означає, що в розподілі частіше зустрічаються нижчі значення ознаки (середнє значення 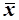 менше серединного Meі модального Мо).
менше серединного Meі модального Мо).
Чим більше величина |As|, тим більше асиметричний розподіл. Оцінна шкала асиметрії:
|As| 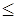 0,25 - асиметрія незначна;
0,25 - асиметрія незначна;
0,25<|As| 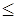 0,5 - асиметрія помітна (помірна);
0,5 - асиметрія помітна (помірна);
|As|>0,5- асиметрія істотна.
Висновок:
Для ознаки вартість активів спостерігається істотнаправостороння асиметрія. Отже, в розподілі переважають вищі значення ознаки.
Для ознаки фінансовий результат спостерігається істотнаправостороння асиметрія. Отже, в розподілі переважають вищі значення ознаки.
2.Показник ексцесу Ekхарактеризує крутизну кривої розподілу - її загостреність або пологість у порівнянні з нормальною кривою.
Як правило, коефіцієнт ексцесу обчислюється тільки для симетричних або близьких до них розподілів.
Якщо Ek>0, то вершина кривої розподілу розташовується вище за вершину нормальної кривої, а форма кривої є більш гостровершинною, ніж нормальна. Це говорить про скупчення значень ознаки в центральній зоні ряду розподілу, тобто про переважну появу серед даних значень, близьких до середньої величини.
Якщо Ek<0, то вершина кривої розподілу лежить нижче за вершину нормальної кривої, а форма кривої пологіша в порівнянні з нормальною. Це означає, що значення ознаки не концентруються в центральній частині ряду, а розсіяні по всьому діапазону від xmax до xmin.
Для нормального розподілу Ek=0.Чим більше абсолютна величина |Ek|, тим істотніше розподіл відрізняється від нормального.
При незначному відхиленні Ek від нуля форма кривої емпіричного розподілу трохи відрізняється від форми нормального розподілу.
Висновок:
1.Оскільки для ознаки Вартість активів Ek>0,то крива розподілу є більш гостровершинною в порівнянні з нормальною кривою. При цьому Ekтрохи відрізняється від нуля (Ek=|0,12|)Отже, за даною ознакою форма кривої емпіричного розподілу трохи відрізняється від форми нормального розподілу.
2.Оскільки для ознаки Фінансовий результат Ek>0,то крива розподілу є більш гостровершинною в порівнянні з нормальною кривою. При цьому Ekзначно відрізняється від нуля (Ek=|3,34|). Отже, за даною ознакою форма кривої емпіричного розподілу значно відрізняється від форми нормального розподілу.
Читайте також:
- I. Постановка завдання статистичного дослідження
- II. Завдання на проект.
- V. ДОМАШНЄ ЗАВДАННЯ
- V. ДОМАШНЄ ЗАВДАННЯ
- V. Завдання.
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- Vi. домашнє завдання
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
| <== попередня сторінка | | | наступна сторінка ==> |
| Завдання 1. | | | III. Економічна інтерпретація результатів статистичного дослідження банків |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |