Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ТМО ознайомлення учнів з геометричними фігурами (точкою, прямою, відрізком, ламаною, многогранниками) та їх найпростішими властивостями.

2.Результати методичних досліджень (роботи М.В.Богдановича, А.М.Пишкала та ін.) свідчать, що недостатня якість геометричних знань є не стільки результатом обмежених пізнавальних можливостей молодших школярів, скільки спричиняється недоліками в реалізації вимог програми та недоліками у системі його вивчення. Оскільки основне завдання вивчення геометричного матеріалу полягає у формуванні у школярів чітких уявлень і первісних понять про геометричні фігури (точка, пряма лінія, ламана лінія, відрізок прямої, кут, многокутник, круг тощо), то вчитель повинен чітко усвідомлювати ТМО цієї роботи.

Вся робота з формування уявлень про геометричні фігури та поняття повинна базуватися на закономірностях, які встановлені психологами та методистами. Серед них вважаємо за необхідне виділити наступні:

1) оскільки перші геометричні відомості у дітей є якісними, а не кількісними, то вчитель повинен ознайомлювати учнів з великою кількістю геометричних об’єктів, не пов’язуючи цю роботу лише з вимірюванням;

2) враховуючи значний запас уявлень про властивості матеріальних об’єктів, вчитель повинен використати це і, абстрагуючись від деяких із цих властивостей, виявляти те спільне, що лежить в основі геометричних уявлень та понять;

3) оскільки відповідно до вимог програми школярі повинні бути ознайомлені з геометричною формою оточуючих предметів, то слід проводити роботу з визначення форми цих предметів;

4) робота з розкриття правильного наукового трактування змісту термінів і понять, що вивчаються, повинна вестися систематично;

5) вчитель повинен підбирати такі предмети, для яких “ознака порівняння” дуже добре помітна і може бути легко виділена учнями;

6) успішне формування такого абстрактного поняття як “геометрична фігура” залежить від різноманітності накопичених учнями уявлень, а тому вчитель повинен, максимально використовуючи наявний досвід дітей, застосовувати найрізноманітніші об’єкти для формування уявлень про геометричні фігури та засвоєння відповідної термінології.

Що є одним із завдань вивчення геометричного матеріалу в початкових класах? –ознайомлення із геометричними фігурами та їх найпростішими властивостями. У процесі цієї роботи вчитель повинен навчити дітей:

- виділяти, називати і правильно показувати вказану геометричну фігуру;

- правильно зображати фігуру на папері і дошці;

- позначати вказану фігуру за допомогою букв;

- при потребі вимірювати відповідну величину, яка пов’язана з цією фігурою.

Чи знайомі діти з геометричними фігурами до школи і які завдання стоять у зв'язку з цим перед вчителем? –оскільки про деякі геометричні фігури учні дещо знають ще до школи, то завдання вчителя у дочисловому періоді полягає в тому, щоб він, показуючи відповідні геометричні фігури або використовуючи їхні зображення, з’ясував, якими знаннями про ці фігури володіють діти: правильними чи неправильними. Після цього він повинен розпочати роботу з уточнення, а якщо потрібно, то і з виправлення, систематизації та узагальнення знань учнів.

Найпершою і найпростішою геометричною фігурою є точка, але вона не має визначення навіть у систематичному курсі геометрії, бо, з одного боку, відноситься до неозначуваних понять, а з іншого - в силу надзвичайно високого ступеня абстрактності. Яких же результатів повинен досягти вчитель, формуючи уявлення дітей про точку? –ознайомлюючи дітей з поняттям “точка”, вчитель повинен навчити учнів виділяти, називати, правильно показувати та зображати на папері і на дошці точку.

Які етапи проходить формування первинних уявлень про точку? – до цих етапів можна віднести принаймні наступні:

1) підготовка дітей до письма цифр і букв, в процесі якої діти ставлять точки на різних лініях, у різних частинах клітинки зошита;

2) використання точок при формуванні уявлень про пряму та криву, коли діти повинні показувати, які точки належать чи не належать відповідній геометричній фігурі;

3) ознайомлення з відрізком, коли на малюнках вони показують точки, які є кінцями відрізка, належать відрізку, знаходяться поза ним тощо;

4) використання уявлень про точку при ознайомленні з многокутником та його елементами;

5) ознайомлення з позначеннями точок і інших геометричних фігур буквами латинського алфавіту.

Яка ж система вправ використовується на кожному етапі? –аналіз системи вправ нині діючих підручників математики для початкових класів, методичних посібників для вчителів, вивчення досвіду роботи класоводів дозволяє виділити наступні завдання на кожному з названих етапів. Так, при підготовці до письма букв і цифр використовуються такі вправи:

а) поставити точку у середині клітини, на верхній стороні, у верхньому правому куті тощо;

б) сполучити точки за зразком, який подано у підручнику, або сполучити їх без зразка. Вже при виконанні цих вправ треба формувати правильні уявлення про точку, а саме: точка це слід, який залишає олівець, ручка, крейда; точка - це перетин двох прямих. Виходячи із цього, треба слідкувати за тим, щоб діти не зображали точку так чи так ●, чи так ○.

При вивченні прямої формуванню уявлень дітей про точку сприяє використання таких вправ:

- поставити точку на прямій, над прямою, під прямою, вище прямої, нижче прямої тощо;

- провести пряму через одну, дві, три точки;

- показати точки, які належать прямій, не належать їй, знаходяться над, під, ліворуч, праворуч прямої. При виконанні таких вправ вчитель повинен слідкувати за тим, щоб діти правильно показували такі точки.

Після того, як діти ознайомляться з відрізком, крім вправ, які використовувались раніше, для формування уявлення про точку використовують ще й такі поняття “початок відрізка”, “кінець відрізка” та вправи:

- побудувати відрізок за зразком, попередньо позначивши його початок і кінець;

- виміряти довжину відрізка, сумістивши, коли потрібно, початок відрізка з початком відліку на лінійці, а кінець відрізка з відповідною поділкою на лінійці;

- побудувати відрізок заданої довжини;

- порівняти відрізки накладанням або за допомогою мірки.

Після того, як діти ознайомляться із поняттями “трикутник”, “чотирикутник”, “п’ятикутник”, “многокутник” для формування уявлення про точку використовують, крім названих раніше, ще й такі вправи:

- показати вершини трикутника, чотирикутника, многокутника;

- поставити точку всередині, зовні, на стороні многокутника;

- побудувати многокутник за зразком чи без нього;

- позначити вершини многокутника точками та сполучити їх відрізками тощо.

Після ознайомлення із колом і кругом формуванню уявлень про точку сприяють наступні вправи:

а) показати або побудувати точку, яка належить колу (кругу), не належить йому;

б) показати центр, радіус, діаметр кола (круга). Аналогічні вправи слід використовувати й при ознайомленні дітей з многогранниками та круглими тілами.

При ознайомленні із позначенням точок буквами латинського алфавіту для формування поняття “точка” використовуються такі вправи:

- позначити вказані точки буквами;

- показати і прочитати вказані точки;

- виписати назви точок, які мають певну властивість. При виконанні таких вправ вчитель повинен слідкувати за тим, щоб діти правильно показували такі точки.

Що повинні знати учні про пряму лінію? – аналіз вимог програми з математики для початкових класів дозволяє твердити, що учні повинні володіти такими знаннями та вміннями, що стосуються прямої:

1) впізнавати пряму лінію, яка накреслена у будь-якому напрямку на площині;

2) відрізняти пряму лінію від кривої та від відрізка;

3) вміти будувати пряму лінію за допомогою лінійки;

4) знаходити аналоги прямої лінії в оточуючій дійсності.

Яка ж система вправ використовується для формування уявлень про пряму? – аналіз системи вправ підручників і методичних посібників для вчителів свідчать, що з цією метою використовуються наступні вправи:

- натягування нитки;

- розгляд прямих на малюнках;

- перегинання аркуша паперу;

- розрізування аркуша паперу;

- спостереження за лініями на аркуші паперу;

- побудова прямих, коли пряма виникає як слід олівця чи крейди.

Які прийоми використовуються при формуванні уявлень про пряму? – враховуючи абстрактний характер поняття “пряма лінія”, вчитель повинен допомогти учням усвідомити сутність уявлення про неї. З цією метою необхідно широко використовувати прийом матеріалізації та прийом зіставлення і протиставлення геометричних образів. Використання цих прийомів дозволить сформувати правильні уявлення про пряму лінію та познайомити школярів з допомогою вказаних вище вправ із основними властивостями прямої та кривої: 1) через одну точку можна провести безліч прямих; 2) через дві точки можна провести єдину пряму; 3) через дві точки можна провести безліч кривих.

Коли і як можна ознайомити учнів з поняттям відрізка прямої? – тоді, коли учні навчаться позначати точки на прямій. Аналіз методичної літератури, вивчення досвіду роботи вчителів-новаторів дозволяє зробити висновок про наявність принаймні двох підходів до введення поняття “відрізок”. Для дітей, які мають невисокий рівень розвитку абстрактного мислення, можна запропонувати наступний підхід до введення поняття відрізок. Вчитель пропонує взяти довгу нитку та туго натягнути її. Після цього пропонуємо двом учням перерізати її у двох місцях. Ту частину прямої, яка знаходиться між двома розрізами, будемо називати відрізком. Отримана таким чином нова геометрична фігура “відрізок” навіть у своїй назві асоціюється із дією, в результаті якої вона утворилася. При другому підходові вчитель креслить на дошці пряму лінію і пропонує учням поставити на ній дві точки. Після цього пропонуємо школярам витерти ті частини прямої, які знаходиться поза точками. Отже, на дошці залишиться лише та частина прямої, яка знаходиться між точками. Вчитель повідомляє, що ми одержали нову геометричну фігуру, яку в математиці прийнято називати відрізок. Після ознайомлення учнів із відрізком розпочинається робота з формування в учнів уявлень про нього.

Які ж вправи і спостереження використовуються при цьому? – аналіз системи вправ підручників з математики, методичних посібників для вчителів, вивчення досвіду роботи вчителів-новаторів дозволяють стверджувати, що з цією метою використовується наступне:

1) відшукання в оточуючій дійсності предметів або їх частин, які нагадують відрізок;

2) показування сторін многокутників чи ланок ламаної лінії;

3) моделювання многокутників;

4) побудова відрізків;

5) вимірювання довжини відрізків;

6) побудова відрізків, які проходять через три точи, які лежать на одній прямій.

У процесі виконання вказаних вправ до свідомості учнів вчитель повинен довести основні відмінності відрізка від прямої, а саме: відрізок обмежений; пряма не обмежена; при побудовах ми зображаємо весь відрізок, але лише частину прямої. Сказане вище дозволяє зробити висновок про те, що формування у школярів уявлень про відрізок проводиться протягом вивчення всього курсу математики у початкових класах.

Які етапи формування уявлень про многокутник?– вивчення методичної літератури дозволяє стверджувати, що формування уявлень дітей про многокутники та їх види проходить принаймні три етапи: а) дошкільний, на якому формування уявлень про многокутники носить безсистемний характер (особливо якщо дитина не відвідує дитячого садочка!); б) шкільний, на якому формування відповідних уявлень має цілеспрямований характер і відбувається спочатку при використанні многокутників як дидактичного матеріалу, а потім у процесі ознайомлення з окремими видами многокутників та їх елементами. Оскільки значна кількість дітей ще до школи знайома з такими фігурами як “кружечок”, “квадратик”, “трикутник”, “прямокутник” тощо, то завдання вчителя у дочисловому періоді полягає в тому, щоб виявити наявні у школярів відомості про ці фігури. Після цього слід провести роботу із систематизації, уточнення чи навіть виправлення наявних уявлень. Зробити це можна тоді, коли вчитель пропонує учням дати відповіді на наступні запитання: яку фігуру виставлено на набірному полотні?, які фігури виставлено на набірному полотні?, виставте на набірне полотно квадрат!, у наборі геометричних фігур знайдіть вказані многокутники тощо. У процесі виконання названих вправ вчителеві необхідно уважно слідкувати за правильністю застосування учнями відповідних термінів: квадрат, трикутник, круг, прямокутник (дітей слід поступово переводити від застосування термінів “квадратик”, “кружечок” тощо до вказаних раніше!).

Яка система вправ використовується з метою формування уявлень молодших школярів про многокутники?– аналіз системи завдань підручників і методичних посібників для вчителів дозволяють виділити наступні:

- показування елементів многокутника (при цьому особливу увагу слід звернути на правильність показування, постійно ставлячи перед учнями наступні запитання: як правильно показати вершину?, як правильно показати сторону?, як правильно показати кут?);

- моделювання многокутників із лічильних паличок чи іншого роздаткового матеріалу;

- розфарбовування многокутників;

- побудова многокутників (пропонуємо студентам виконати завдання № 24для самостійної роботи);

- знаходження многокутників на предметах оточуючої дійсності. При виконанні вказаних вправ вчитель повинен забезпечувати різноманітність використовуваних многокутників за розмірами, матеріалом виготовлення, розміщенням на площині, кольором тощо. Нехтування цією вимогою призводить до формування неправильних уявлень.

Як же ознайомлюють дітей з кожним новим видом многокутників? – ТМО цієї роботи аналогічні для кожного нового виду многокутника. Саме тому розкриємо їхню сутність на прикладі ознайомлення учнів з трикутником, оскільки він є першим видом многокутників. Систематична робота з формування уявлень дітей про трикутник розпочинається на уроці, де діти вивчають число і цифру 3. Демонструючи школярам трикутник, вчитель проводить з ними бесіду: яку фігуру виставлено на набірному полотні (зображено на малюнку)? – трикутник. Чи можете Ви сказати, чому цю фігуру називають трикутником? – бо у нього три кути. Після цього вчитель демонструє, як правильно слід показувати кути (прикладаючи указку до однієї сторони трикутника, вчитель, не відриваючи її від вершини, повертає її доти, доки вона не суміститься з іншою стороною трикутника, або указкою проводить дужку від однієї сторони трикутника до іншої), сторони (прикладаючи кінець указки до однієї вершини, вчитель проводить нею по стороні трикутника до іншої вершини) і вершини (кінець указки повинен суміщатися з вершиною кута). Скільки сторін у трикутника? – три. Скільки вершин у трикутника? – три. Чи могли б Ви придумати іншу назву для цієї фігури? – тристоронник, тривершинник. Після ознайомлення з трикутником та його елементами розпочинається систематична робота з формування уявлень про нього. З цією метою використовується відповідна система вправ (щоб засвоїти ТМО роботи над кожним видом вправ, пропонуємо студентам виконати завдання № 25для самостійної роботи).

В яких значеннях застосовується термін “кут” в математиці? – як відомо, в геометрії термін “кут” застосовують у різних значеннях: 1) у значенні “плоский кут”, під яким розуміють частину площини, обмежену двома променями, що виходять із однієї точки; 2) для позначення двогранного кута, під яким розуміють частину простору, яка обмежена двома півплощинами, що мають спільну пряму; 3) для позначення многогранного кута. Цілком зрозуміло, що у початкових класах не можна говорити про жоден із названих кутів, бо учням ще невідомі поняття, через які вони означаються. У зв'язку зі сказаним постає питання про таке трактування поняття “кут”, яке б, з одного боку, не суперечило науковому його розумінню, а з іншого – було доступне для сприйняття молодшими школярами.

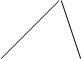
Як трактується це поняття в курсі математики початкових класів? – враховуючи вищесказане, в курсі математики початкових класів термін “кут” застосовується у розумінні “відірваного кута многокутника”. Таке розуміння не суперечить науковому трактуванню поняття плоского кута та дозволяє сформувати в учнів І-ІУ класів правильне уявлення про кут. Сказане обумовлює те, що модель кута з’являється на очах у дітей в результаті відривання одного або й всіх по одному кутів трикутника чи неопуклого п’ятикутника (див. малюнок № 13.1.).

З якими ж моделями кутів зустрічаються молодші школярі? – спочатку це моделі довільних кутів, які отримуються в результаті відривання кутів многокутників. При ознайомленні з прямим кутом з’являється модель прямого кута, яка використовується при побудові прямих кутів, при відшуканні прямих кутів многокутників і при визначенні виду чотирикутника. Як же одержати модель прямого кута? – згинанням аркуша паперу невизначеної форми. Пропонуємо дітям взяти аркуш паперу і зігнути його у довільному напрямку (спочатку цю операцію демонструє вчитель, а потім її має обов’язково виконати кожен учень самостійно!). Після цього вчитель показує, як ще раз слід перегнути аркуш паперу та пропонує виконати цю операцію кожному школяреві самостійно. Виконавши відповідні дії, вчитель пояснює, що кут, який ми отримали, в математиці називають прямим. Пропонуємо дітям порівняти величини прямих кутів, які отримані із різних аркушів паперу (попередньо вчитель демонструє як слід виконувати порівняння). Учні з подивом встановлюють, що всі прямі кути рівні, незважаючи на те, що вони одержані з різних аркушів паперу. Таким чином, практично встановлено: всі прямі кути рівні. Після цього школярі використовують модель прямого кута для відшукання прямих кутів у многокутниках, а пізніше для встановлення виду чотирикутника (прямокутник – не прямокутник) та для побудови прямих кутів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
ТМО вивчення геометричного матеріалу в курсі математики І-ІУ-х класів.	\|	Малюнок № 13.1.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.009 сек.