
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Визначення закону руху динамічної моделі.
Положення|становище| ланок динамічної моделі визначається двома узагальненими координатами і . Рівняння руху динамічної моделі запишемо у вигляді умов кинетостатического| рівноваги ланок 1 і 2:
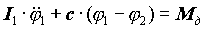 , ,  . .
| (21.1) |
Розділимо перше рівняння системи на I1, а друге - на I2, і отримаємо:
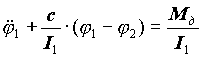 , , 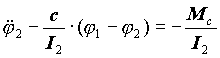 . .
| (21.2) |
Перетворимо рівняння системи таким чином. Віднімемо і першого рівняння (21.2) друге, а потім підсумуємо рівняння (21.1). Тоді системи рівнянь запишеться|занотовуватиме| в наступному|слідуючому| вигляді|виді|:
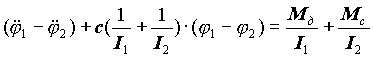 , ,  . .
| (21.3) |
Позначимо деформацію пружного зв'язку . Її друга похідна за часом, звідки . Позначимо також:
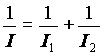 або і .
або і .
Підставимо ці позначення в (21.3) і отримаємо|одержуватимемо|:
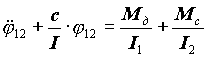 , , 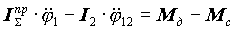 . .
| (21.4) |
Пружні вимушені|змушені| коливання в системі.
Перше рівняння системи містить|утримує| тільки|лише| координату деформації пружного зв'язку і описує пружні коливання в системі, друге включає і координату пов'язану з рухом системи без деформації . Розглянемо|розглядуватимемо| вирішення першого рівняння системи при наступних|слідуючих| початкових|вихідних| даних:
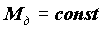 , .
, .
З урахуванням|з врахуванням| цього перше рівняння системи (21.4) запишеться|занотовуватиме| так:
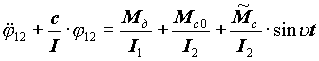 . (21.5)
. (21.5)
Введемо|запроваджуватимемо| наступні|такі| позначення

а також: і , і підставимо в (21.5):
 . (21.6)
. (21.6)
Вирішення цього рівняння при і початкових умовах :
 , (21.7)
, (21.7)
| де: | 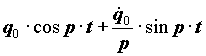 - вільні коливання з частотою p - вільні коливання з частотою p 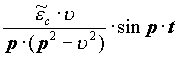 - гармонійні коливання з частотою p і з амплітудою залежної від - гармонійні коливання з частотою p і з амплітудою залежної від  - вимушені коливання з частотою обурюючої сили - вимушені коливання з частотою обурюючої сили 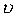 . .
|
Читайте також:
- CMM. Визначення моделі зрілості.
- I визначення впливу окремих факторів
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- Ocнoвнi визначення здоров'я
- S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
- А. Визначення розмірів і площі зони хімічного зараження.
- Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
- Алгебраїчний спосіб визначення точки беззбитковості
- Алгоритм визначення проекцій точок на поверхнях обертання
- Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
- Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
| <== попередня сторінка | | | наступна сторінка ==> |
| Кінематика хвилевого механізму | | | Визначення власних частот коливань системи. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |