РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Виникнення (походження) держави. 6 страница
| № п/п | Назва. | Рівняння. | ||
| 1. | Загальне рівняння прямої. | 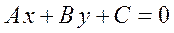
| ||
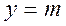
| Пряма, паралельна осі Ох | |||
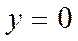
| Вісь Ох | |||
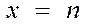
| Пряма, паралельна осі Оу | |||
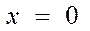
| Вісь Оу | |||
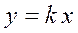
| Пряма, що проходить через початок координат. | |||
| 2. | Рівняння прямої у відрізках | 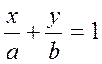
| ||
| 3. | Рівняння прямої з кутовим коефіцієнтом |  , ,
| 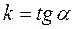 - кутовий коефіцієнт прямої. - кутовий коефіцієнт прямої.
| |
| 4. | Рівняння прямої, що проходить через дві точки  і і 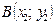
| 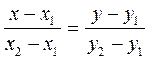
| ||
| 5. | Рівняння прямої з нормальним вектором |
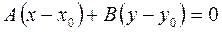
| 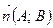 -нормальний вектор прямої; -нормальний вектор прямої;
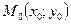 - точка, через яку проходить пряма - точка, через яку проходить пряма
| |
| 6. | Канонічне рівняння прямої. |  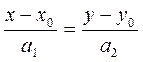
|  - направляючий вектор прямої; - направляючий вектор прямої;
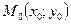 - точка, через яку проходить пряма - точка, через яку проходить пряма
| |
| 7. | Параметричні рівняння прямої | 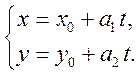
| ||
| 8. | Взаємне розміщення двох прямих: | |||

| 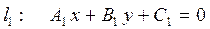
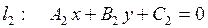
| 
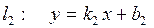
| ||
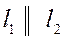
| 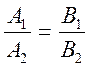
| 
| ||
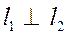
| 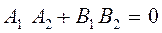
| 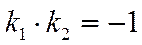
| ||
4. Розв’язання систем лінійних рівнянь за формулами Крамера
Для системи n лінійних рівнянь з n невідомими (над довільним полем)
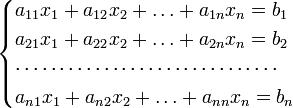
з визначником матриці системи Δ, що не рівний нулеві, розв'язок записується у такому вигляді:
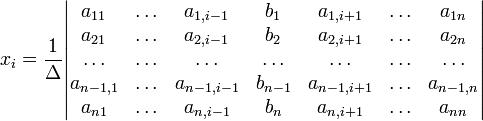
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів).
Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c1, c2, …, cn виконується рівність:
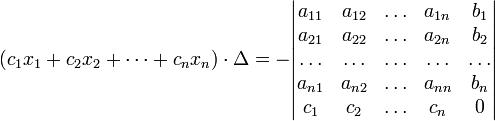
У такій формі формула Крамера справедлива без припущення, що Δ не рівне нулю.
Приклад:
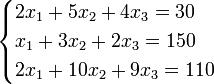
Визначники:
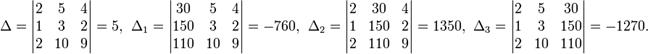
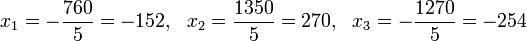
5. Приклади для розв’язування.
І. Визначте координати векторів:
1. 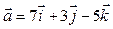 2.
2. 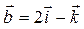
3.  4.
4. 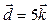
5. 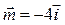 6.
6. 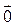
2. Відомі координати точок
А(4; -3; 2), В(-2; 4; -3), М(0; 5; 1) та N(-4; 0; -3). Знайдіть координати векторів, 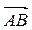 ,
, 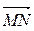 , їх модулі та косинус кута між ними.
, їх модулі та косинус кута між ними.
3. Відомі координати векторів  . Знайдіть координати та модулі векторів:
. Знайдіть координати та модулі векторів:
1. 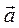 +
+ 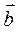 ;
;
2. 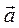 +
+  ;
;
3. 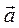 +
+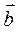 -
-  ;
;
4. 3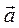 ;
;
5. - 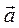 +2
+2 ;
;
6. 2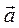 +3
+3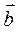 - 2
- 2  ;
;
4. Користуючись умовою колінеарності двох векторів, перевірте, чи колінеарні вектори:
1. 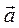 (2/5; -1/3; 4/5) та
(2/5; -1/3; 4/5) та 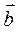 (3/5; - 1/2; 6/5)
(3/5; - 1/2; 6/5)
2. 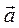 (-6; 1/3; 3) та
(-6; 1/3; 3) та 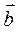 (-2; 1/9; -1/3)
(-2; 1/9; -1/3)
5. За яких значень n та p вектори 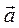 та
та 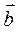 будуть колінеарними?
будуть колінеарними?
1. 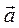 (-3; n; 4) та
(-3; n; 4) та 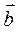 (-2; 4; р)
(-2; 4; р)
2. 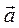 (4; n; -4) та
(4; n; -4) та 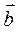 (р; -2; 1/2 )
(р; -2; 1/2 )
6. Знайдіть периметр трикутника, вершини якого задані координатами
А(8; 0; 6), В(8; -4; 6), С(6; -2; 5). Визначте вид трикутника.
7. Відрізок АВ заданий координатами кінців А(4; 2; -3) та В(6; -4; -1). Знайдіть координати точки С, яка ділить відрізок:
1. навпіл;
2. у співвідношенні 1:3;
3. у співвідношенні 2:5;
8. Доведіть, що чотирикутник з вершинами А(1; 4; 3), В(2; 3; 5), С(2; 5; 1) та D(3; 4; 3) – паралелограм.
10. Обчислити кути нахилу до осі Ох прямих:  ,
,  ,
, 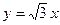 .
.
11. Скласти рівняння прямої,яка проходить через початок координат, якщо кутовий коефіцієнт дорівнює 1; 2: -1: 4.
12. Скласти рівняння прямої, яка проходить через початок координат і утворює з віссю Ох кут: 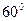 ,
, 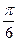 ,
, 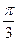 .
.
13. Знайти кутові коефіцієнти прямих, заданих рівняннями: 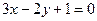 ,
, 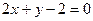 ,
, 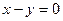 .
.
14. Скласти рівняння прямої, яка проходить через точку А і перпендикулярна вектору 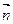 :
:
a. 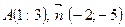
b. 
c. 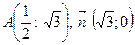
15. Скласти рівняння прямої, яка перетинає вісь Ох в точці 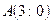 , а вісь Оу – в точці
, а вісь Оу – в точці 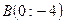 .
.
16. Обчислити площу трикутника, який відтинається прямою 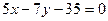 від координатного кута.
від координатного кута.
17. При якому значенні 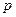 задані прямі паралельні і перпендикулярні:
задані прямі паралельні і перпендикулярні:
a. 
b. 

18. Дано 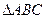 . Знайти:
. Знайти:
a. рівняння сторін;
b. довжини сторін;
c. рівняння медіани АМ;
d. довжину медіани АМ;
e. рівняння висоти 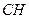 ;
;
f. точку перетину медіани АМ і висоти 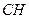 ;
;
g. 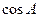 ;
;
h. зробити малюнок.
1. 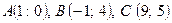
2. 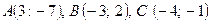
3. 
4. 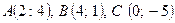
9. Розв’язування систем лінійних рівнянь за формулами Крамера та методом Гауса.
1. 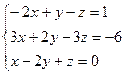 2.
2. 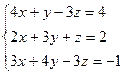 3.
3. 
4. 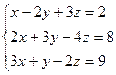 5.
5. 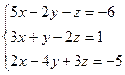 6.
6. 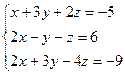
7. 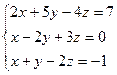 8.
8. 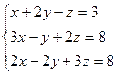 9.
9. 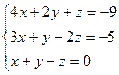
Розділ 8. . СТЕРЕОМЕТРІЯ
1. Основні поняття стереометрії
2. Аксіоми стереометрії
3. Теореми стереометрії.
4. Площі геометричних фігур.
5. Площі поверхонь та об’єми деяких геометричних тіл.
6. Паралельні проекції деяких плоских фігур.
7. Приклади для розв’язування
1. Основні поняття стереометрії
Стереометрія — Стереометрія (від грец. «стереос» — тілесний, «метрео» — вимірюю) — це розділ геометрії, в якому вивчаються фігури в просторі, а також властивості просторових фігур. Основними фігурами в просторі є точка, пряма та площина.
В стереометрії з'являється новий вид взаємного положення прямих: прямі, які схрещуються. Це одне з небагатьох значних відмінностей стереометрії від планіметрії, оскільки в багатьох випадках задачі зі стереометрії вирішуються шляхом розгляду різних площин, в яких виконуються планіметричні закони.
2. Аксіоми стереометрії
Аксіома 1
Якщо пряма має з площиною дві спільні точки, то вона належить цій площині
Аксіома 2
Якщо дві площини мають спільну точку, то вони або збігаються, або перетинаються по прямій, яка проходить через цю точку.
Аксіома 3
Через три точки, що не лежать на одній прямій проходить лише одна площина.
Аксіома B1
Паралельними звуться прямі, що не перетинаються і лежать в одній площині
Аксіома B2
Прямі, що не перетинаються і не лежать в одній площині звуться мимобіжними
Аксіома B3
Якщо пряма не лежить на площині і не перетинається з нею, то пряма паралельна площині
Аксіома B4
Дві площини називаються паралельними, якщо вони не перетинаються.
Аксіома B5
Пряма перпендикулярна до площини, якщо вона перетинаючись з цією площиною, утворює прямий кут з кожною прямою проведеною в цій площині через точку перетину прямої і площини.
3. Теореми стереометрії
Теорема 1
Через пряму і точку, що не лежить на цій прямій проходить площина, причому тільки одна.
Теорема 2
Через дві прямі, що перетинаються проходить площина, причому тільки одна.
Теорема 3
Через дві паралельні прямі можна провести площину, причому тільки одну.
Теорема 4
Якщо пряма L1, що не лежить на площині P паралельна прямій L2, що належить площині P, то L1 паралельна площині P.
4. Площі геометричних фігур.
| Фігура | Співвідношення між елементами | |||||
Прямокутний трикутник
    
| 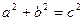 теорема Піфагора теорема Піфагора
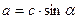
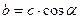
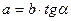
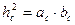
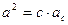
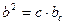
| 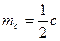
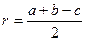
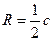
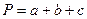
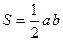
| ||||
Трикутник
| 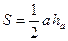 , , 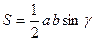
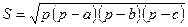 - формула Герона, - формула Герона, 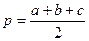
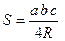 , , 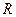 - радіус описаного кола - радіус описаного кола
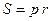 , , 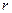 - радіус вписаного кола - радіус вписаного кола
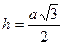 , ,  - для правильного трикутника. - для правильного трикутника.
| |||||
Прямокутник
| 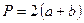
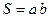
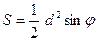
| |||||
Квадрат
| 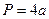
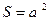
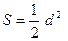
| |||||
Паралелограм
     
| 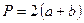

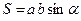
| 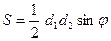
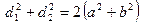
| ||||
Ромб
|
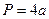
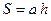
| 
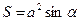
| ||||
Трапеція
| 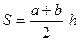
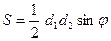
| 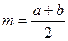 - довжина середньої лінії - довжина середньої лінії
| ||||
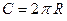 - довжина кола - довжина кола
| 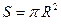 - площа круга - площа круга
| |||||
5. Площі поверхонь та об’єми геометричних тіл.
| Назва | Зображення | Площа поверхні | Об’єм |
| Призма |
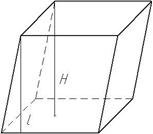
| Sбічної=P l P- периметр l- висота бічної грані | V=Sоснови H Н- висота призми |
| Піраміда |
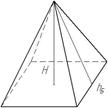
|
Sбічної=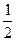 P hбічної
Р – периметр основи P hбічної
Р – периметр основи
|
V=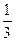 Sоснови H Sоснови H
|
| Зрізана піраміда |
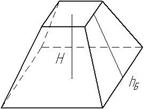
|
Sбіч=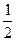 (P1+Р2) hбіч
Р1 , Р2 – периметри основ (P1+Р2) hбіч
Р1 , Р2 – периметри основ
|
V=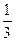 (S1+ (S1+ +S2) H
S1 ,S2 – площі основ +S2) H
S1 ,S2 – площі основ
|
| Циліндр |

| Sбічн=2πRH | V=πR2 H |
| Конус |
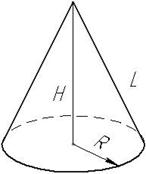
| Sбічн=πRL L - твірна |
V=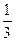 πR2 H πR2 H
|
| Зрізаний конус |
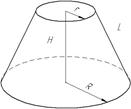
| Sбічн=π(R+r)L |
V=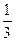 π(R2+Rr+r2) H π(R2+Rr+r2) H
|
| Сфера, куля |
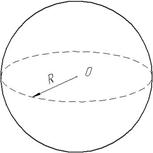
| S=4πR2 |
V=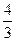 πR3 πR3
|
| Кульовий сектор |
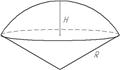
| ---- |
V=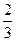 πR2 H πR2 H
|
| Кульовий сегмент |
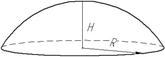
| S=2πRH |
V=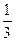 πH2 (3R-H) πH2 (3R-H)
|
6. Паралельні проекції деяких плоских фігур.
| проекція – трикутн ик будь – якої форми | |||||||||||||||||||||||||||||
| проекція –паралелограм будь – якої форми | |||||||||||||||||||||||||||||
| проекція – трапеція будь – якої форми | |||||||||||||||||||||||||||||
 
| проекція кола - еліпс |
7.Приклади для розв’язування
Читайте також:
- I. ОБРАЗОВАНИЕ СОЕДИНЕННЫХ ШТАТОВ 14 страница
- XVII ст.). Виникнення козацтва.
- А. В. Дудник 1 страница
- А. В. Дудник 10 страница
- А. В. Дудник 11 страница
- А. В. Дудник 12 страница
- А. В. Дудник 2 страница
- А. В. Дудник 3 страница
- А. В. Дудник 4 страница
- А. В. Дудник 5 страница
- А. В. Дудник 6 страница
- А. В. Дудник 7 страница
| <== попередня сторінка | | | наступна сторінка ==> |
| Виникнення (походження) держави. 5 страница | | | Виникнення (походження) держави. 7 страница |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |