
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
План-конспект урока 2 страница
Позначають 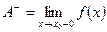
Функція 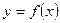 називається неперервною в точці
називається неперервною в точці 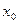 ,якщо виконуються слідуючи умови:
,якщо виконуються слідуючи умови:
1) функція визначена в точці 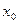 і в деякому околі цієї точки;
і в деякому околі цієї точки;
2) існують односторонні границі 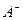 і
і 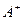 ;
;
3) односторонні границі рівні між собою і дорівнюють значенню функції в точці 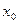 .
.
5. Приклади для розв’язування.
1. Обчислити границі.
1) 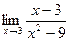
2) 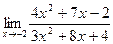
3) 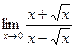
4) 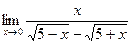
5) 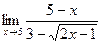
6) 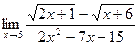
7) 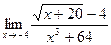
8) 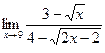
9) 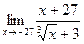
10) 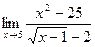
11) 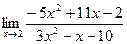
12) 
13) 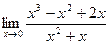
14) 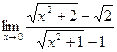
15) 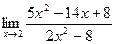
16) 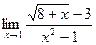
17) 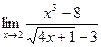
18) 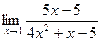
19) 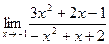
20) 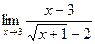
21) 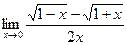
22) 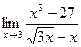
23) 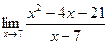
24) 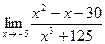
25) 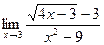
26) 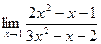
2. Дослідити функцію на неперервність і побудувати графік.
1. 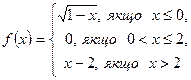
1.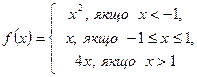
2.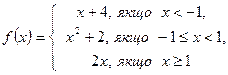
3.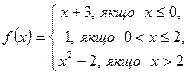
4.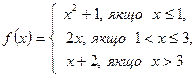
5.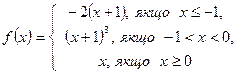
6.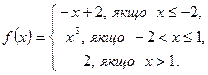
7.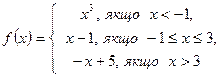
8.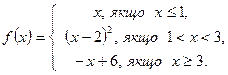
9. 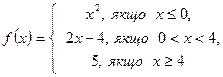
3. Обчислити границі функції в точці та на нескінченності:
1. 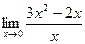 5.
5. 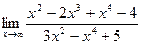
2. 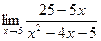 6.
6. 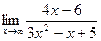
3. 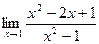 7.
7. 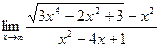
4. 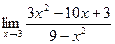 8.
8. 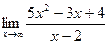
Розділ 3. ТРИГОНОМЕТРІЯ
1. Визначення тригонометричних функцій
2. Графіки тригонометричних функцій
3. Основні співвідношення
4. Знаки тригонометричних функцій по четвертях
5. Таблиця значень тригонометричних функцій деяких кутів
6. Основні формули тригонометрії.
7. . Найпростіші тригонометричні рівняння
8. Приклади для розв’язування.
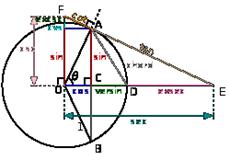
1. Визначення тригонометричних функцій
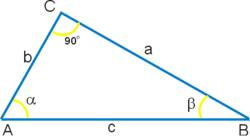 Тригонометричні функції можна визначити розглянувши прямокутний трикутник. Косинусом кута називається відношення довжини прилеглого катета до довжини гіпотенузи.
Тригонометричні функції можна визначити розглянувши прямокутний трикутник. Косинусом кута називається відношення довжини прилеглого катета до довжини гіпотенузи.
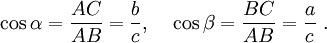
Тангенсом кута називається відношення довжини
протилежного катета до довжини прилеглого катета:

Котангенсом кута називається відношення
довжини прилеглого катета до довжини протилежного катета:
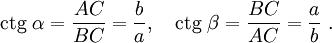
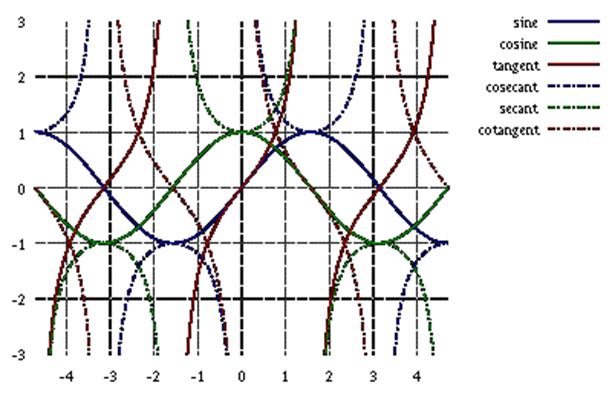
2. Графіки тригонометричних функцій
3. Основні співвідношення
Наступне співвідношення випливає із теореми Піфагора:
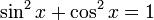
З урахуванням визначення , маємо як наслідок
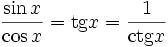
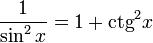
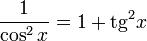
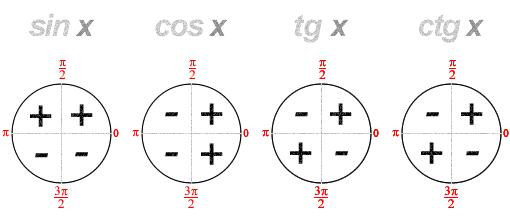
5. Знаки тригонометричних функцій по четвертях
5. Таблиця значень тригонометричних функцій деяких кутів
| α | 00 | 300 | 450 | 600 | 900 | 1800 |
| 0 рад | π/6 рад | π/4 рад | π/3 рад | π/2 рад | π рад | |
| Sin α | 1/2 | 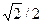
| 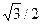
| |||
| cos α | 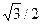
| 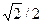
| 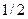
| |||
| tg α | 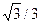
| 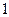
| 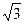
| Не існ. | ||
| ctg α | Не існ. | 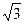
| 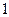
| 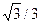
| Не існ. |
Слід пам’ятати:
sin ( - α) = - sin α arcsin ( - α) = - arcsin α
cos ( - α) = cos α arccos ( - α) = π - arccos α
tg ( - α) = - tg α arctg ( - α) = - arctg α
ctg ( - α) = - ctg α arcctg ( - α) = π - arcctg α
sin ( α +2πk) = sin α
cos ( α +2πk) = cos α
tg ( α +πk) = tg α
ctg ( α +πk) = ctg α
. Основні формули тригонометрії.
І. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ СУМИ ДВОХ АРГУМЕНТІВ ( ФОРМУЛИ ДОДАВАННЯ
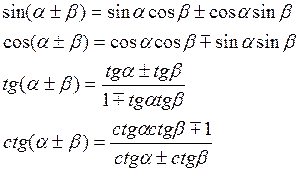
ІІ. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ПОДВОЄНОГО АРГУМЕНТА.
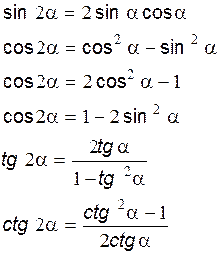
ІІІ. ФОРМУЛИ ЗНИЖЕННЯ СТЕПЕНІ.
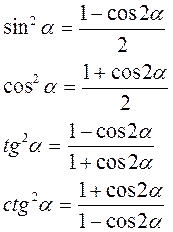
ІV/. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ПОЛОВИННОГО АРГУМЕНТА.
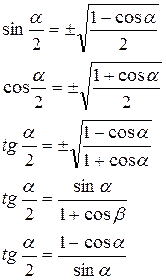
V. ПЕРЕТВОРЕННЯ ДОБУТКУ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ НА СУМУ.
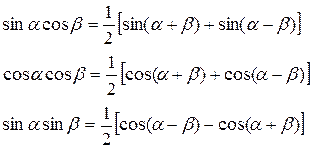
VI. ПЕРЕТВОРЕННЯ СУМИ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ НА ДОБУТОК.
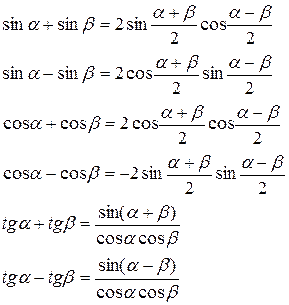

7. «Найпростіші тригонометричні рівняння»
| № п/п | Вид рівняння | Розв’язки | Приклад |
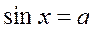
| Якщо 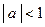 , то , то 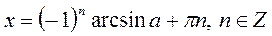 Якщо
Якщо 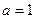 , то , то 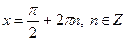 Якщо
Якщо 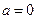 , то , то 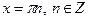 Якщо
Якщо 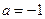 , то , то 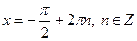
| 
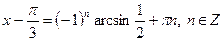 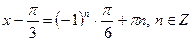
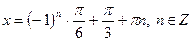
| |
| 2. |
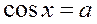
| Якщо 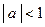 , то , то 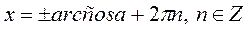 Якщо
Якщо 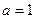 , то , то 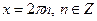 Якщо
Якщо 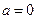 , то , то 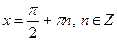 Якщо
Якщо 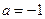 , то , то 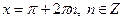
| 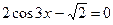 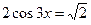
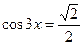
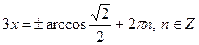
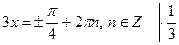
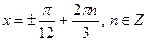
|
| 3. |
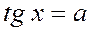
| 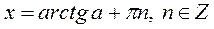 Якщо
Якщо 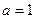 , то , то 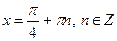 Якщо
Якщо 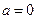 , то , то 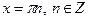 Якщо
Якщо 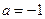 , то , то 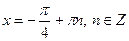
| 
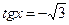
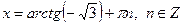
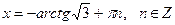 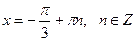
|
| 4. |
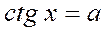
| 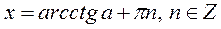 Якщо
Якщо 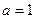 , то , то 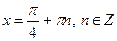 Якщо
Якщо 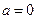 , то , то 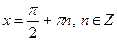 Якщо
Якщо 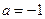 , то , то 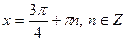
| 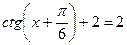  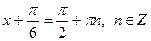
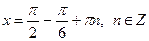
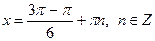
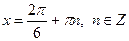
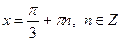
|
8. Приклади для розв’язування.
1. Виразити дані тригонометричні функції через функції аргумента, що вдвічі менші від даного.
1) 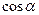
2) 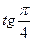
3) 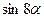
4) 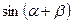
5) 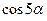
6) 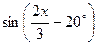
2. *Дано: 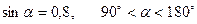
Знайти: 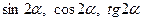
3. **Довести, що
1) 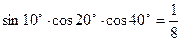
2) 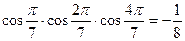
4. Спростити.
1) 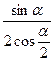
2) 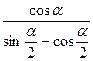
3) *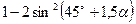
4) *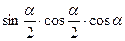
5) **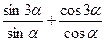
6) **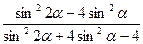
7) **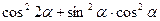
8) **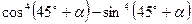
5. Довести тотожність.
1) ***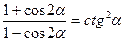
2) ***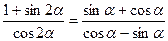
3) ***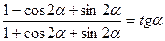
6. Знайти значення виразу.
1) 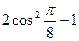
2) 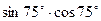
3) 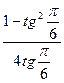
4) 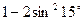
7. Розв’яжіть найпростіші тригонометричні рівняння
1) sin x =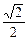 2 cos 2x =1 sin
2 cos 2x =1 sin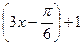 = 0
= 0
2) cos x = -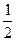
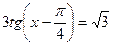
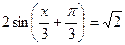
3) ctg 3x = 4 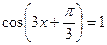
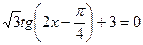
4) 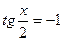
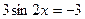
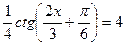
5) sin 3x = 1 2 cos (4x) =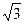
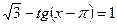
6) 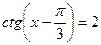 sin 2x +1 =0
sin 2x +1 =0 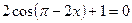
8. **Розв’язати рівняння, права частина яких нуль,
а ліва розкладається на множники.
1. 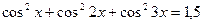
2. 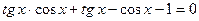
3. 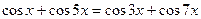
4. 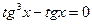
5. 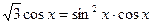
6. 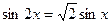
7. 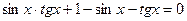
8. 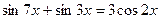
9. 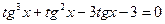
10. 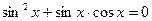
9.*** Розв’язати однорідні тригонометричні рівняння.
1. 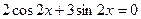
2. 
3. 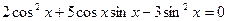
4. 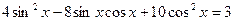
5. 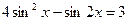
6. 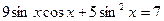
7. 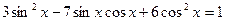
8. 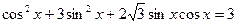
9. 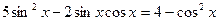
10. 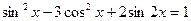
11. 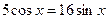
12. 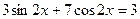
13. 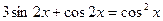
14. 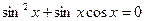
15. 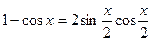
Розділ 4. СТЕПЕНІ ТА ЛОГАРИФМИ
1. Поняття степені з дійсним показником та кореня n-го степеню
2. Властивості степенів .
3. Властивості коренів.
4. Поняття логарифму .
5. Властивості логарифмів
6. Приклади для розв’язування.
1. Степені. Корінь n-го степеня.
| | 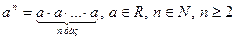
| Степінь з натуральним показником |
| | 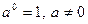
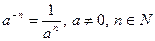
| Степінь з цілим показником |
| | 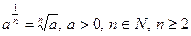
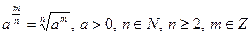
| Степінь з дробовим показником |
| 2. Властивості степенів. | ||
| | 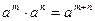
| 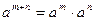
|
| | 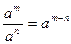
| 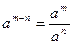
|
| | 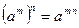
| 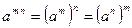
|
| | 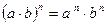
| 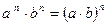
|
| | 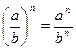
| 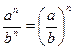
|
| | 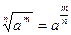
| 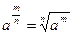
|
| | 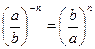
| |
| 3. Властивості кореня n-го степеня. | ||
| |  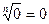 , , 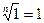
| |
| | 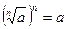 - за означенням - за означенням
| |
| | 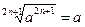 - для будь-яких - для будь-яких 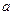
| 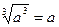
|
| | 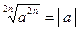
| 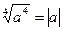
|
| | 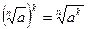
| |
| | 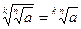
| Корінь з кореня |
| | 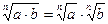
| Корінь із добутку |
| | 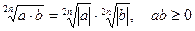
| Корінь парного степеня із добутку |
| | 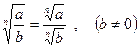
| Корінь із частки |
| | 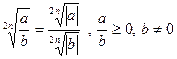
| Корінь парного степеня із частки |
| | 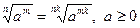
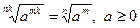
| Основна властивість коренів |
4. Поняття логарифмів .
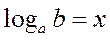 ,
бо ,
бо 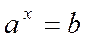
| Логарифмом додатного числа 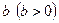 за основою за основою 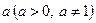 називається показник степеня, до якого треба піднести називається показник степеня, до якого треба піднести 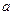 , щоб одержати , щоб одержати 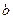 . .
| |
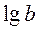
| Десятковий логарифм, 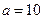
| |
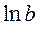
| Натуральний логарифм, 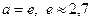
| |
| 5. Властивості логарифмів. | ||
| 1. | 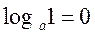
| |
| 2. | 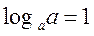
| |
| 3. | 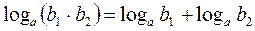
| 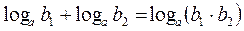
|
| 4. | 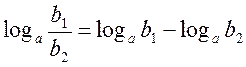
| 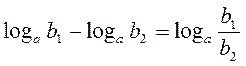
|
| 5. | 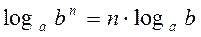
| 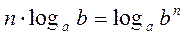
|
| 6. | 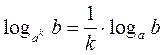
| 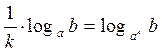
|
| 7. | Якщо 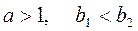 , то , то 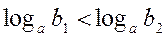
| |
| 8. | Якщо 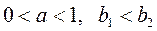 , то , то 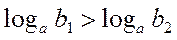
| |
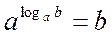
| Основна логарифмічна тотожність | |
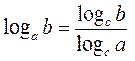 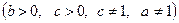
| Формула переходу від однієї основи логарифма до іншої | |
| Наслідки | ||
1) 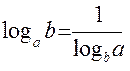 2)
2) 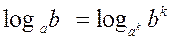 3)
3) 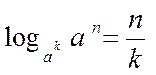
|
Читайте також:
- I. ОБРАЗОВАНИЕ СОЕДИНЕННЫХ ШТАТОВ 14 страница
- А. В. Дудник 1 страница
- А. В. Дудник 10 страница
- А. В. Дудник 11 страница
- А. В. Дудник 12 страница
- А. В. Дудник 2 страница
- А. В. Дудник 3 страница
- А. В. Дудник 4 страница
- А. В. Дудник 5 страница
- А. В. Дудник 6 страница
- А. В. Дудник 7 страница
- А. В. Дудник 8 страница
| <== попередня сторінка | | | наступна сторінка ==> |
| План-конспект урока 1 страница | | | План-конспект урока 3 страница |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |