
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Домашнє завдання
7.1. Знайти: МХ і DX.
X 5 10 15 20
P 1/12 4/12 5/12 1/6
7.2. Дано: X 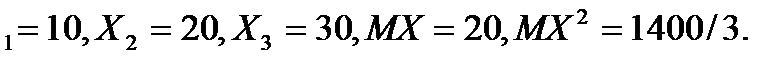 Знайти:
Знайти: 
7.3. Дано: 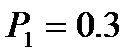 , MX=3.4, DX=0.84. Знайти:
, MX=3.4, DX=0.84. Знайти: 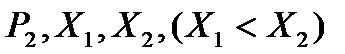
7.4. Сім разів підкинуто монету. Знайти математичне сподівання та середнє квадратичне відхилення кількості появи герба.
7.5. Ймовірність того, що студент відповість на питання дорівнює 0,7. Білет містить три питання. Знайти середнє значення кількості питань, на які студент відповість.
7.6. У хімчистці стверджують, що 85% плям на вовняних речах відмиваються. Ви здали в хімчистку 3 вовняні речі з плямами. Скласти закон розподілу кількості ваших вовняних речей, що після хімчистки виявились без плям. Знайти математичне сподівання і дисперсію.
7.7. Неперервна випадкова величина рівномірно розподілена на інтервалі (4;6). Знайти М(Х), D(Х), σ(Х) цієї величини.
7.8. Обчислити М(Х), D(Х), σ(Х) випадкової величини Х, якщо щільність розподілу відома :
0, x  (– ∞ ; 0)
(– ∞ ; 0)
f(x) =
3e-3x, x  [0 ;+ ∞)
[0 ;+ ∞)
7.9. Обчислити М(Х), D(Х), σ(Х) випадкової величини Х, якщо щільність розподілу відома
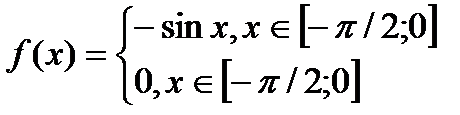 .
.
7.10. Обчислити М(Х), D(Х), σ(Х), якщо відома функція розподілу випадкової величини:
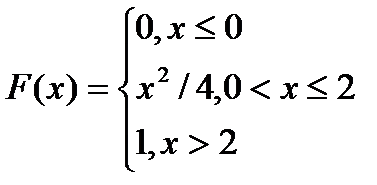 .
.
7.11. Знайти дисперсію та середнє квадратичне відхилення показникового розподілу, заданого щільністю розподілу  ,
,  .
.
Лекція 8 Закон великих чисел. Центральна гранична теорема
Розглянемо нерівність Чебишева : відхилення випадкової величини від її математичного сподівання не може бути дуже великим, воно обмежене. Точніше, великі відхилення мають малу ймовірність : 
P(|X -MX|>  ) <
) < 
Дуже часто ми декілька разів повторюємо експеримент по виміру якої–небудь величини, а потім беремо середнє арифметичне тих значень, що одержали. Виявляється, що чим більше вимірів, тим це середнє арифметичне все ближче наближається до математичного сподівання. Це і є закон великих чисел- середнє багатьох експериментів вирівнюється, випадковість змінюється закономірністю.
У формі Чебишева закон великих чисел має вигляд :
Нехай Х1, Х2, . . . , Хn . . . – однаково розподілені незалежні випадкові величини з математичними сподіваннями і дисперсіями
MX1 = MX2 = …. = MXn = …. = m
DX1 = DX2 = … = DX n= … = d
тоді для будь - якого  >0
>0
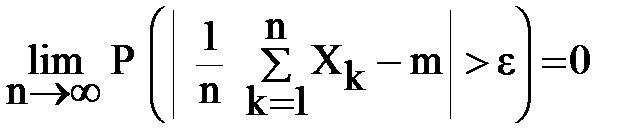 (8.1)
(8.1)
Це означає, що при використанні великої кількості доданків ймовірність відхилення середнього арифметичного від математичного сподівання стає все меншою.
Перша форма закону великих чисел належить Я.Бернуллі, вона стосується “схеми Бернуллі”. Застосовуємо до цього випадку співвідношення (8.1). За величину  приймаємо одну з незалежних випадкових величин, що має розподіл імовірностей
приймаємо одну з незалежних випадкових величин, що має розподіл імовірностей
P (A) = 
Маємо MX1 = р, DX1 = р(1-р); реалізація випадкової величини. 
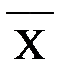 – кількість появи випадкової події А, тобто частота
– кількість появи випадкової події А, тобто частота  (n – число випробувань, k– число появи А), m = p – ймовірність появи випадкової події А. За умов (8.1)
(n – число випробувань, k– число появи А), m = p – ймовірність появи випадкової події А. За умов (8.1)
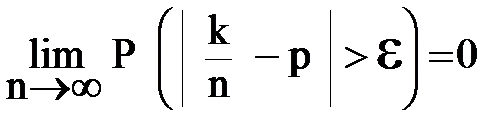 ,це і є закон великих чисел Бернуллі.
,це і є закон великих чисел Бернуллі.
Перейдемо до центральної граничної теореми.
Досліджуючи схему Бернуллі виявляється, що випадкова величина
х = 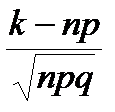 наближено розподілена за нормальним законом. Подібне твердження справедливе і для ряду інших випадків; зветься воно центральною граничною теоремою. Перші кроки в одержані цього результату зробив П.Л. Чебишев. За його пропозицією спробу, і причому успішну, довести цю теорему зробили учні Чебишева О.М. Ляпунов та А.А. Марков. Ляпунов першим одержав це доведення, він довів наступний результат : нехай незалежні випадкові величини Х1, Х2 , .. .., Хn мають скінченні математичні сподівання mk = MXk і дисперсії
наближено розподілена за нормальним законом. Подібне твердження справедливе і для ряду інших випадків; зветься воно центральною граничною теоремою. Перші кроки в одержані цього результату зробив П.Л. Чебишев. За його пропозицією спробу, і причому успішну, довести цю теорему зробили учні Чебишева О.М. Ляпунов та А.А. Марков. Ляпунов першим одержав це доведення, він довів наступний результат : нехай незалежні випадкові величини Х1, Х2 , .. .., Хn мають скінченні математичні сподівання mk = MXk і дисперсії
σk2 = dk = DXk, причому виконується умова
 (8.2)
(8.2)
Позначимо  (8.3)
(8.3)
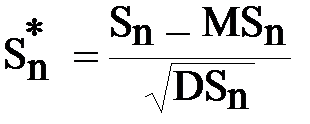 (8.4)
(8.4)
Тоді випадкова величина 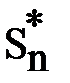 при великих n наближено розподілена за нормальним законом з математичним сподіванням m = 0 і σ = 1, а саме
при великих n наближено розподілена за нормальним законом з математичним сподіванням m = 0 і σ = 1, а саме
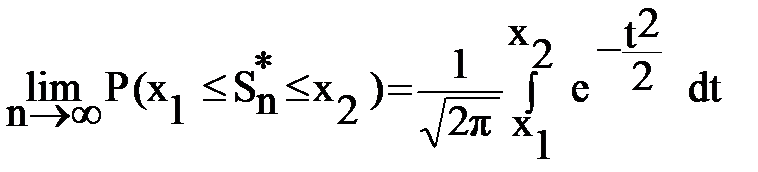
Розглядають суми S* незалежних випадкових величин (8.3), які нормуються за допомогою (8.4). Ці нормовані суми Sn* розподілені наближено нормально, коли число доданків велике, а внесок, що дає кожний доданок, відносно малий, - саме такий зміст має умова (8.2 ).
Центральна гранична теорема пояснює , чому нормальний розподіл часто зустрічається у застосуваннях: він, звичайно, з’являється тоді, коли сумується багато випадкових величин, кожна з яких відносно невелика. Наприклад, це має місце, коли при вимірі якоїсь величини одержати точне значення заважають багато дрібних похибок, що сумуються між собою. За природних умов ці похибки компенсують одна одну так, що у результаті для остаточної похибки наближено справедливий нормальний розподіл. Теорію похибок вперше детально вивчали К.Ф.Гаусс і А.М. Лежандр. У результаті « накладання» випадкових величин не завжди з’являється величина розподілена нормально, граничним розподілом може бути (при певних умовах) розподіл Пуассона та інші.
Лекція 9 Завдання математичної статистики. Генеральна сукупність і вибірка. Варіаційний ряд. Графічне зображення вибірки
Масові випадкові явища підпорядковані закономірностям, що встановлюються на основі вивчення статистичних даних - результатів спостережень.
Математична статистика займається розробкою методів реєстрації, опису і аналізу таких даних, її теоретичною базою служить теорія ймовірностей. У задачах математичної статистики ми маємо деякі результати спостережень, і шукається математична модель, здатна дати опис цих результатів.
Деякі основні задачі, розв'язування яких становить завдання математичної статистики:
1. За обмеженим об'ємом експериментальних даних встановити закон розподілу випадкової величини.
2. Знайти параметри передбачуваного закону розподілу.
3. Оцінити, наскільки обраний закон розподілу погоджується з результатом експерименту.
4. Оцінити, надійність обчислених параметрів.
5. Встановити наявність залежності між випадковою величиною і дати цій залежності кількісну характеристику.
6. Описати аналітично залежність між випадковими величинами.
При вивчені характеристики деякої сукупності об'єктів часто не можна перевірити усі такі об'єкти; може статися, що цих об'єктів дуже багато. Може бути і інше - при вивчені характеристики сам об'єкт псується. Наприклад, для перевірки на міцність деякої деталі її розривають; якщо всі деталі перевірити, то всі вони і будуть знищені, - тому перевіряють лише невелику кількість деталей, а про інші судять, виходячи з цієї перевірки.
ОзначенняГенеральною сукупністю називається множина усіх однорідних одиниць, що мають якісну спільність, вибіркою - деяка кількість елементів цієї множини, відібраних певним засобом.
Вибірка повинна вірно представляти генеральну сукупність, її характерні риси. Наприклад, якщо мова йде про інтереси громадян даної країни (генеральна сукупність), то для досліду не можна брати тільки молодь або лише людей з вищою освітою тощо. Існують спеціальні методи для того, щоб вибірка адекватно відображала генеральну сукупність, або, як кажуть, була показною. Число n елементів вибірки називається її об'ємом.
Нехай з генеральної сукупності вилучена вибірка, і у кожного з вибраних елементів замірялась якась характеристика х (це може бути, наприклад, зріст людини або міцність деталі);нехай значення x1 спостерігалось m1 разів; x2-m2разів,... , xk-mk разів, тоді об'єм вибірки 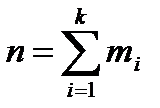 .
.
Значення xi, що спостерігаються, називаються варіантами, числа спостережень mi - частотами, а відношення цих чисел до об'єму вибірки 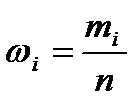 - відносними частотами.
- відносними частотами. 
Послідовність варіант, записаних у зростаючому порядку з вказівкою відповідних їм частот, називається статистичним рядом розподілу.
Статистичний розподіл можна задати також у вигляді послідовності інтервалів (розрядів) і відповідних їм частот (відносних частот), - частота, відповідна інтервалові, дорівнює сумі частот варіант, що попали у цей інтервал. Так роблять у випадку, коли число різних варіант дуже велике.
Наприклад,
1.
| xi | -1 | |||||
| mi | 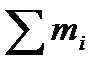 = 100 = 100
| |||||

| 0,05 | 0,1 | 0,4 | 0,3 | 0,15 |  = 1 = 1
|
2.

| (2;4) | (4;6) | (6;8) | (8; 10) | |
| mi | 3О | 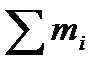 =100 =100
| |||

| 0,2 | 0,4 | 0,3 | 0,1 |  = 1 = 1
|
Якщо у прямокутній системі координат Ох  зобразити точки (xi;
зобразити точки (xi;  ) і сполучити сусідні точки відрізками, то одержимо ламану, що зветься полігоном відносних частот. У випадку інтервального ряду розподілу користуються гістограмою. Для її побудови на осі абсцис відкладають інтервали. На кожному з них, як на основі, будують прямокутник з висотою, рівною
) і сполучити сусідні точки відрізками, то одержимо ламану, що зветься полігоном відносних частот. У випадку інтервального ряду розподілу користуються гістограмою. Для її побудови на осі абсцис відкладають інтервали. На кожному з них, як на основі, будують прямокутник з висотою, рівною 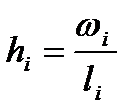 , де
, де  - довжина і-го інтервалу;
- довжина і-го інтервалу;  - висота прямокутника.
- висота прямокутника.
Площа кожного прямокутника збігається з відносною частотою 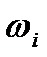 , а сумарна площа усіх прямокутників дорівнює 1. У теорії ймовірностей – аналог – площа під щільністю розподілу дорівнює 1.
, а сумарна площа усіх прямокутників дорівнює 1. У теорії ймовірностей – аналог – площа під щільністю розподілу дорівнює 1.
При збільшенні об'єму вибірки п інтервали можна зробити все більш дрібними. При цьому полігон і ламана, що обмежує гістограму, наближаються до плавних кривих, які близькі до теоретичної характеристики розподілу - графіку щільності неперервного розподілу f(х). Таким чином, полігон і гістограма дають наочне уявлення про закон розподілу випадкової величини.
Читайте також:
- V. ДОМАШНЄ ЗАВДАННЯ
- V. ДОМАШНЄ ЗАВДАННЯ
- V. Завдання.
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
| <== попередня сторінка | | | наступна сторінка ==> |
| Властивості дисперсії | | | Домашнє завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |