• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Частинні похідні та повний диференціал

ЛЕКЦІЯ 12: ДИФЕРЕЦІЙОВАНІСТЬ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ

Частинною похідною від функції 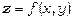за незалежною змінною х називається скінчена границя

,

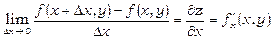обчислена при постійному у.

Частинною похідноювід функції 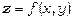за незалежною змінною у називається скінчена границя

,

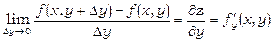обчислена при постійному х.

Для частинних похідних справедливі звичайні правила та формули диференціювання.

Приклади 1. Знайти частинні похідні функцій:

а) ; б) .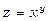

а) Розглядаючи у як постійну величину, отримаємо 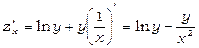. Розглядаючи х як постійну, знайдемо .

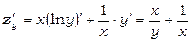б) При фіксованому у маємо степеневу функцію від х. Таким чином, 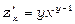. При фіксованому х функція є показниковою відносно у,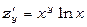

Приклад 2. Обсяг витрат продажу нового продукту z залежить від часу х та витрат у підприємства на рекламу. Якщо х вимірювати тижнями, а у у гривнях, тоді ця залежність матиме вигляд

.

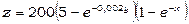Знайти 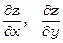та вказати економічний зміст цих похідних при х=1 і у=400.

Маємо

,

.

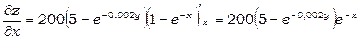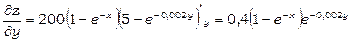При х=1 і у=400 отримаємо

,

.

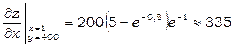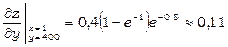Частинна похідна 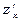характеризує швидкість зміни обсягу продажу нового продукту за тиждень, коли витрати на рекламу не змінюються.

Частинна похідна 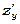характеризує швидкість зміни обсягу продукту при зміні суми витрат на рекламу і постійному х. За один тиждень при витратах на рекламу 400 гривень швидкість зростання обсягу продажу продукту буде 0,11.

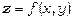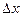Повним приростомфункції в точці М(х,у) називається різниця , де і 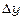- довільні прирости аргументів.

Повним диференціалом функції 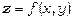називається сума добутків частинних похідних цієї функції та приростів відповідних незалежних змінних, тобто

.

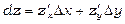Формулу диференціала можна записати у вигляді

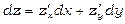
або .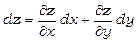

Функція 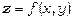називається диференційовною в точці (х,у), якщо її повний приріст може бути представлений у вигляді

,

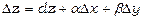де dz – диференціал функції, 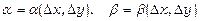- нескінченно малі при .

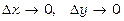При досить малих значеннях 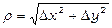для диференційованої функції 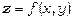справедливі наближені рівності

.

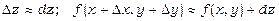Ці формули застосовують для наближених обчислень приростів функції або наближених значень функції в деякій точці.

Приклад 3. 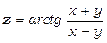. Знайти dz.

Знайдемо частинні похідні:

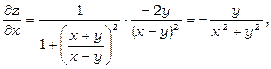
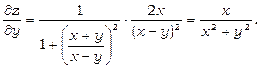
Значить, .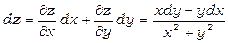

Приклад 4. Обчислити наближено .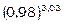

Шукане число можна розглядати як значення функції 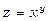при 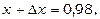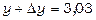, де х=1, у=3,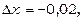 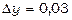. Знайдемо значення z при х=1, у=3; маємо 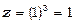.Знаходимо приріст функції:

Значить, .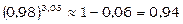

Читайте також:

1. Види робочого часу: нормальний, скорочений і неповний.
2. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
3. Головна передача, диференціал, півосі (приводні вали) і маточини ведучих коліс
4. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.
5. Диференціал функції
6. Диференціал функції.
7. Диференціали вищих порядків.
8. Диференціальна діагностика.
9. Диференціальна діагностика.
10. Диференціальна діагностика.
11. Диференціальна імпульсно-кодова модуляція. Дельта модуляція
12. Диференціальна рента

Переглядів: 6793