РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Формула Стокса
Нехай задано векторне  .
.
Якщо функції  неперервні разом зі своїми частинними похідними 1-го порядку на поверхні
неперервні разом зі своїми частинними похідними 1-го порядку на поверхні 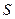 і
і  – замкнений контур, який обмежує поверхню
– замкнений контур, який обмежує поверхню 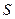 , то справедлива формула Стокса
, то справедлива формула Стокса


Цій формулі можна надати векторний зміст
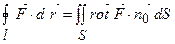 .
.
Тобто циркуляція по замкненому контуру  дорівнює потоку ротора через поверхню
дорівнює потоку ротора через поверхню 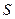 , яка натягнута на контур
, яка натягнута на контур  .
.
Задача 30. Знайти похідну функції 
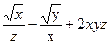 унапрямі вектора
унапрямі вектора в т.
в т. 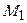 та
та 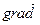
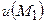 ,якщо
,якщо  ,
, 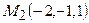 .
.
Розв’язання: Похідну функції  у напрямі вектора
у напрямі вектора  в точці
в точці 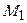 обчислюємо за формулою:
обчислюємо за формулою:
 ,
,
де 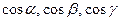 – напрямні косинуси вектора
– напрямні косинуси вектора  .
.
Знайдемо вектор  , довжина якого
, довжина якого 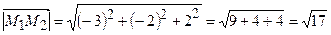 .Напрямні косинуси вектора
.Напрямні косинуси вектора  :
:  .
.
Знайдемо частинні похідні першого порядку функції 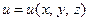 в точці
в точці 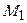 :
:  ;
;
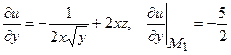 ;
; 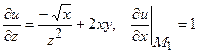 .
.
Маємо:
 .
.
Градієнт функції 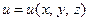 в точці
в точці 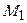 знайдемо за формулою:
знайдемо за формулою:
 . Маємо
. Маємо
 .
.
Задача 31. Знайти похідну скалярного поля  в точці
в точці  в напрямі, який йде до точки
в напрямі, який йде до точки  .
.
Розв’язання: Для знаходження похідної за напрямом скористаємось формулою  . Знайдемо одиничний вектор заданого напрямку :
. Знайдемо одиничний вектор заданого напрямку :
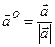 ,
, 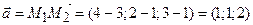 ,
,
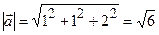 ,
,  , тобто маємо
, тобто маємо  .
.
Знайдемо значення частинних похідних в точці 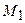 .
.
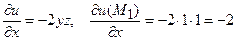 ,
,
 ,
,
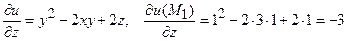
Отже маємо  .
.
Задача 32. Знайти  ,
, 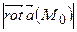 та
та 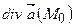 для векторного поля
для векторного поля 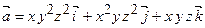 , де точка
, де точка 
Розв’язання: За означенням ротор векторного поля 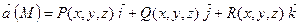 в довільній точці
в довільній точці 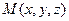 знаходиться за формулою:
знаходиться за формулою:
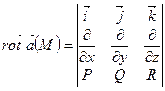 .
.
Маємо
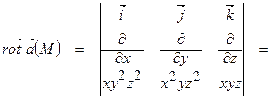
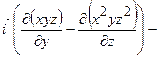


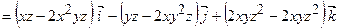
Знайдемо ротор в точці 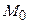 і його модуль
і його модуль  ,
, 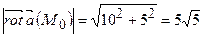 . За означенням, дивергенція векторного поля
. За означенням, дивергенція векторного поля 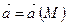 в довільній точці
в довільній точці 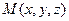 знаходиться за формулою:
знаходиться за формулою:  . В нашому випадку
. В нашому випадку

Дивергенція в точці 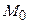 :
:  .
.
Задача 33. Знайти в точці 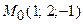 дивергенцію і ротор векторного поля
дивергенцію і ротор векторного поля 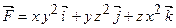 .
.
Розв’язання: Для заданого векторного поля 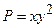 ,
,  ,
,  . Тоді
. Тоді 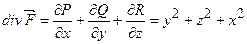 ,
, 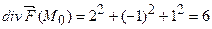
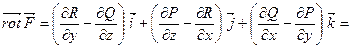
 .
.
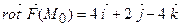 .
.
Задача 34. Обчислити потік векторного поля
 через зовнішню поверхню піраміди, створену площиною
через зовнішню поверхню піраміди, створену площиною  та координатними площинами, двома способами: а) за означенням; б) за допомогою формули Остроградського - Гаусса.
та координатними площинами, двома способами: а) за означенням; б) за допомогою формули Остроградського - Гаусса.
Розв’язання: а) Запишемо рівняння площини у відрізках  і побудуємо її. Маємо піраміду
і побудуємо її. Маємо піраміду 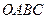 . Обчислимо потік за допомогою поверхневого інтеграла
. Обчислимо потік за допомогою поверхневого інтеграла  , де
, де 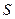 –
–
|
зовнішня поверхня піраміди 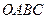 . Обчислимо потік через кожну грань піраміди:
. Обчислимо потік через кожну грань піраміди:
1)  лежить у площині
лежить у площині  і має рівняння
і має рівняння 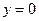 . Нормальний вектор
. Нормальний вектор 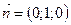 ,
,  ,
,  :
:

 . Знайдемо
. Знайдемо 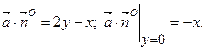 Потік через
Потік через  :
:

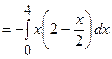
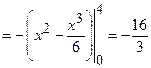 ;
;
2) лежить у площині
лежить у площині 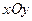 і має рівняння
і має рівняння 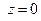 . Нормальний вектор
. Нормальний вектор  . Так як мається на увазі зовнішня сторона, то
. Так як мається на увазі зовнішня сторона, то  .
. 
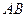 :
:  . Знайдемо
. Знайдемо 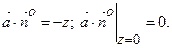 Потік через
Потік через 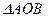 :
:
 ;
;
3)  лежить у площині
лежить у площині 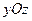 і має рівняння
і має рівняння 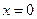 . Нормальний вектор
. Нормальний вектор 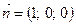 . Так як мається на увазі зовнішня сторона, то
. Так як мається на увазі зовнішня сторона, то  ,
, 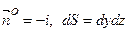 ,
, 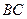 :
:  . Знайдемо
. Знайдемо  Потік через
Потік через  :
:


 ;
;
4)  належить площині
належить площині 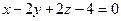 . Нормальний вектор площини
. Нормальний вектор площини  . Знайдемо орт нормального вектора:
. Знайдемо орт нормального вектора:
 . Диференціал поверхні визначається формулою:
. Диференціал поверхні визначається формулою: 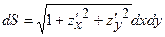 . Маємо
. Маємо 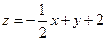 і
і
 . Тоді
. Тоді  . Знайдемо
. Знайдемо 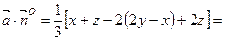
 .
.
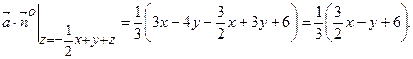
Слід площини  в площині
в площині 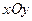 – це пряма
– це пряма 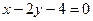 Þ
Þ 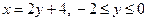 . Потік через
. Потік через  :
:




 .
.
Потік через повну поверхню піраміди 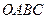 :
:
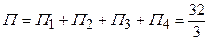 .
.
б) за формулою Остроградського – Гаусса  , де
, де  ,
, 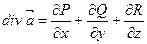 .
.
Знайдемо частинні похідні:

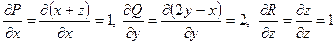 ,
, 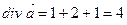 . Інтеграл
. Інтеграл 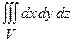 дорівнює об’єму піраміди
дорівнює об’єму піраміди 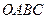 . Маємо
. Маємо 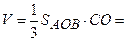

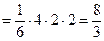 . Тоді
. Тоді  .
.
Задача 35. Обчислити циркуляцію векторного поля
 по контуру трикутника, який з¢являється внаслідок перетину площини
по контуру трикутника, який з¢являється внаслідок перетину площини 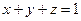 з координатними площинами, при додатному напрямку обходу відносно нормального вектора
з координатними площинами, при додатному напрямку обходу відносно нормального вектора  цієї площини двома способами: а) за означенням; б) за формулою Стокса.
цієї площини двома способами: а) за означенням; б) за формулою Стокса.
Розв’язання:
|
Побудуємо площину 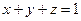 , маємо D
, маємо D  .
.
а) за означенням циркуляція
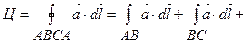

1) на відрізку 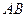 маємо:
маємо: 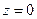 ,
,  ,
,  ,
, 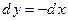

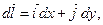
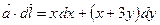 .
.

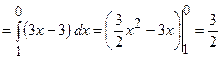 ;
;
2) на відрізку 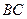 маємо:
маємо: 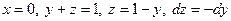
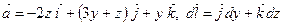 ,
, 

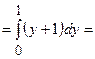
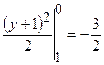 ;
;
3) на відрізку 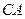 маємо:
маємо: 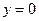 ,
, 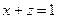 ,
,  ,
, 
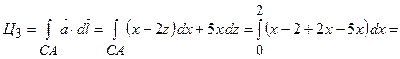
 .
.
Маємо  .
.
б) Обчислимо циркуляцію векторного поля за формулою Стокса:
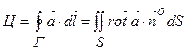 ,
,
де  .
.
Ротор векторного поля обчислюємо за формулою
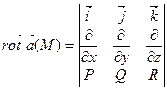 ,
, 
у випадку, коли поверхня 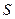 проектується у площину
проектується у площину 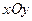 .
.
Знайдемо ротор заданого векторного поля
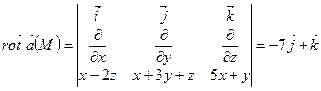
В нашому випадку поверхня 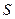 – частина площини, обмеженої
– частина площини, обмеженої  , який лежить у площині
, який лежить у площині 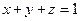 . Нормальний вектор площини
. Нормальний вектор площини 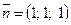 забезпечує потрібний напрям орієнтації поверхні. Орт цього вектора
забезпечує потрібний напрям орієнтації поверхні. Орт цього вектора  Знайдемо
Знайдемо
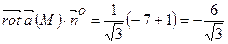 . З рівняння площини маємо
. З рівняння площини маємо
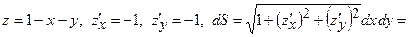

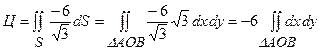 . Інтеграл
. Інтеграл 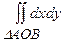 дорівнює площі
дорівнює площі 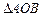 :
:  . Тоді
. Тоді 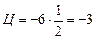 .
.
Задача 36. а) Обчислити за формулою Остроградського – Гаусса потік векторного поля 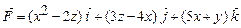 через повну зовнішню поверхню трикутної піраміди, яка обмежена поверхнями
через повну зовнішню поверхню трикутної піраміди, яка обмежена поверхнями 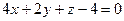 ,
, 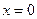 ,
, 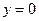 ,
, 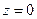 . б) Обчислити за формулою Стокса циркуляцію векторного поля по сторонах трикутника
. б) Обчислити за формулою Стокса циркуляцію векторного поля по сторонах трикутника  в додатному напрямі (проти годинникової стрілки, коли дивитися з кінця нормального вектора).
в додатному напрямі (проти годинникової стрілки, коли дивитися з кінця нормального вектора).
Розв’язання: Запишемо рівняння площини 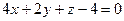 у відрізках
у відрізках 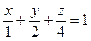 і побудуємо її. Маємо піраміду
і побудуємо її. Маємо піраміду 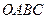 з вершинами у точках
з вершинами у точках  .
.
а) Обчислимо потік через повну поверхню користуючись формулою Остроградського – Гаусса. Для цього знайдемо дивергенцію векторного поля:  .
.
 |
Тоді
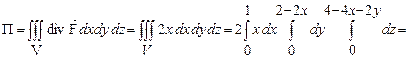
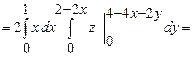
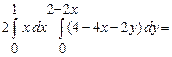
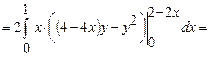
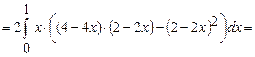

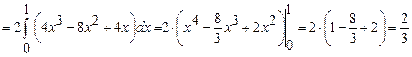 .
.
б) Знайдемо циркуляцію користуючись формулою Стокса

де поверхня 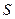 натягнута на контур
натягнута на контур  . За поверхню
. За поверхню 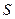 візьмемо поверхню, яка складається з трикутників
візьмемо поверхню, яка складається з трикутників  . Напрям нормалей на цих трикутниках буде співпадати з напрямом осей координат. Знайдемо вектор
. Напрям нормалей на цих трикутниках буде співпадати з напрямом осей координат. Знайдемо вектор  .
.

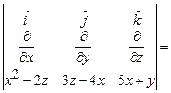

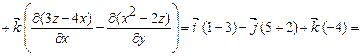
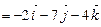 .
.
Тоді 
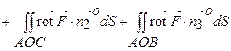
На поверхні  нормальний одиничний вектор
нормальний одиничний вектор  , елемент поверхні
, елемент поверхні 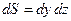 . Тому
. Тому
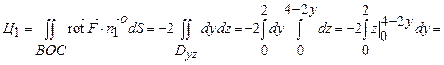
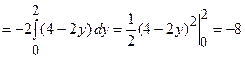 .
.
На поверхні  нормальний одиничний вектор
нормальний одиничний вектор 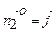 , елемент поверхні
, елемент поверхні 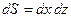 . Тому
. Тому
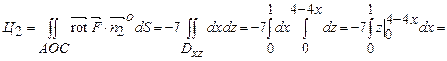
 .
.
На поверхні  нормальний одиничний вектор
нормальний одиничний вектор  , елемент поверхні
, елемент поверхні 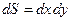 . Тому
. Тому
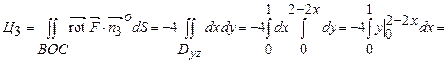
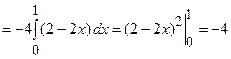 .
.
Таким чином маємо 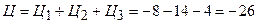 .
.
Можна спростити обчислення циркуляції, якщо врахувати  і контур
і контур  – це трикутник
– це трикутник 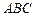 , який належить площині
, який належить площині 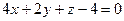 . Нормальний вектор площини
. Нормальний вектор площини 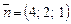 забезпечує потрібний напрям орієнтації поверхні. Орт цього вектора
забезпечує потрібний напрям орієнтації поверхні. Орт цього вектора 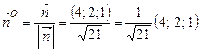 . Знайдемо
. Знайдемо 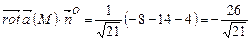 . З рівняння площини матимемо:
. З рівняння площини матимемо: 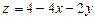 . Тоді
. Тоді 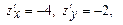
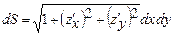

 . Інтеграл
. Інтеграл  дорівнює площі
дорівнює площі 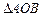 :
:
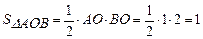 . Тоді
. Тоді  .
.
Читайте також:
- I. Формула спеціальності
- I. Формула спеціальності
- I. Формула спеціальності
- Абсолютні й відносні посилання у формулах
- Барометрична формула
- Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі
- ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ВНУТРІШНЬОГО ТЕРТЯ РІДИНИ МЕТОДОМ СТОКСА
- Вступне звернення і заключна формула ввічливості
- Втрати енергії вздовж круглого трубопроводу. Формула Пуазейля і коефіцієнт Дарсі.
- Грування, тобто має місце формула
- Диференціальне рівняння Нав’є – Стокса
- Загальна формула для визначення переміщень. Метод Мора
| <== попередня сторінка | | | наступна сторінка ==> |
| Формула Остроградського – Гаусса | | | Н. В. Ліманська |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |