• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Приклад 2 1 страница

Виконаємо розрахунок статичного режиму телевізійного антенного підсилювача ДМВ, поданого на Рис. 9.20, виходячи з умов його експлуатації. Елементи L1,C1,C2 утворюють фільтр верхніх частот, який придушує потужні сигнали телебачення метрового діапазону і запобігає перевантаженню підсилювача.

Необхідно визначити опори резисторів за таких умов:

1. Задано тип транзистора (тобто відома сім’я його ВАХ).
2. Відоме значення U_ke0, що забезпечує максимальну термостабільність транзистора.
3. Відомий струм колектора i_k0, що забезпечує мінімум шумів транзистора.
4. Задана напруга джерела живлення.

Складемо розрахункову схему для сталого струму (Рис. 9.20), вилучивши з вихідної схеми кола з конденсаторами, и складемо для неї систему рівнянь

Для спрощення розрахунку припустимо, що . Спрощення придатне для активного режиму роботи транзистора. За сім’єю вихідних ВАХ (Рис. 9.21) визначаємо необхідний базовий струм 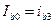і знаходимо опір R₁ з третього рівняння системи

Через одержану робочу точку та точку Е на осі напруг проводимо навантажувальну пряму і у місці її перетину з віссю струмів знаходимо I_кз. Далі

9.3.2. Розрахунок у динамічному режимі.

Розрахунок використовується для визначення параметрів лінійного підсилювача, що працює у режимі малого сигналу, тобто зміни струмів і напруг у колі відбуваються у околі робочих точок, де характеристики достатньо лінійні. Це дозволяє з достатньою точністю замінити нелінійні елементи лінійними, що описуються динамічними (диференціальними) параметрами. Значення цих параметрів залежать від вибору положення робочих точок на ВАХ нелінійних елементів. Запишемо систему рівнянь ВАХ

і розкладемо їх у ряд Тейлора у околі точок статичного режиму. У розкладі обмежимося двома першими членами ряду, припускаючи, що нелінійність ВАХ у околі робочих точок мала.

(9.20)

Диференційні параметри

(9.21)

називаються h- параметрами схеми з спільним емітером. Прирости струмів та напруг у формулі (20) є саме змінними у часі струмами і напругами, що діють у транзисторі, коли до нього, крім джерела живлення, підімкнено джерело змінного струму або напруги, тобто

.

Тому рівняння для цих складових струмів і напруг транзистора можна подати у вигляді

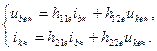(9.22)

Фізичний зміст h- параметрів ясний з рівнянь (22):

У сучасних транзисторів . За цієї умови можна від рівнянь (22) перейти до лінійної еквівалентної схеми транзистора для змінного струму, поданої на Рис. 9.22.

Перетворення, подібні до (20), (22), можна виконати для інших схем ввімкнення транзистора і одержати Z-, Y- , або інші системи параметрів. Враховуючи, що усі системи параметрів описують той самий транзистор, між ними повинно бути однозначне співвідношення. Ці переходи від одної системи параметрів до іншої виконують за допомогою матричних перетворень, наведених у книзі В.П. Сігорського та А.І. Петренка „Основи теорії електронних схем”.

Реальні транзистори окрім активних параметрів містять цілу низку реактивних компонентів еквівалентної схеми, параметри яких є функціями дії та реакції. На не дуже високих частотах (до десятків МГц), у малосигнальному режимі найбільший вплив має ємність колекторного кола С_к і більш реальна еквівалентна схема має вигляд, поданий на Рис. 9.23.

9.4. Підсумки та самоконтроль

У цьому розділі розглянуто нелінійні неінерційні ЕМК, які містять двополюсні та чотириполюсні нелінійні елементи. Розглянуто режими постійних струмів, малого та великого сигналів, можливості апроксимації ВАХ нелінійних елементів. Введено визначення статичних, диференціальних параметрів. Подано рівняння, що описують струми і напруги у транзисторі за допомогою малосигнальних параметрів, та лінійну еквіваленту схему транзистора, що відповідає цим рівнянням.

Поглибити знання за тематикою цього розділу можна, скориставшись літературою [1, §§ 10.1, 10.2], [2, p. 9], [3, гл. 10], [4, гл. 12], [7, розд. 1.5], [12, гл. 4,5,6].

Проконтролювати засвоєння матеріалу цього розділу можна, відповівши на такі питання:

1. Що таке статичні та диференціальні параметри? У яких режимах вони використовуються?
2. Як розуміти поняття «від’ємний опір» ?
3. Як складається повна система рівнянь нелінійного кола і чим вона відрізняється від такої для лінійного кола?
4. Як графічно розв’язують рівняння нелінійного кола? Як будують навантажувальну пряму?
5. У чому полягає задача апроксимації нелінійної характеристики?
6. Що являють собою сім’ї характеристик нелінійних елементів?
7. Якими сім’ями характеристик описуються біполярні та польові транзистори?
8. Як визначити параметри лінійної еквівалентної схеми, скориставшись сім’ями ВАХ транзистора?
9. Як визначити параметри лінійної еквівалентної схеми транзистора експериментально?

10. СИГНАЛИ І ЗАВАДИ В РАДІОЕЛЕКТРОННИХ СИСТЕМАХ

10.1. Основні визначення

Інформація – це сукупність відомостей про процес, подію або предмет, які зменшують недостатність знань про їхні властивості, які були у споживача інформації до одержання повідомлення.

Повідомлення – це матеріальна форма подання інформації. У телекомунікаційних системах під повідомленнями розуміють:

1. Змінні в часі струми і напруги, що виникають на виході вимірювальних перетворювачів (сенсорів, давачів) під час дії на них джерела інформації (це, наприклад, мікрофон, оптична голівка, магнітний зчитувач тощо).

2. Послідовності кодових груп символів, пов'язаних з коливаннями на виході вимірювальних перетворювачів якимось правилом перетворення (кодування).

Сигнал – це фізичний процес, що переносить повідомлення від джерела до споживача. Для виконання функції перенесення повідомлення сигнал повинен мати дві суттєві властивості:

1. стійку ознаку, притаманну даному конкретному сигналові, що відрізняє його від усіх інших сигналів;
2. сигнал завжди є випадковим процесом, бо несе невідому споживачеві інформацію.

Для поєднання таких суперечливих вимог повідомлення втілюється в зміну параметрів сигналу відносно їх середніх значень. Саме середні значення параметрів сигналів і є їх стійкими ознаками (середні частота, часове положення, відстань, кутове положення тощо). Амплітуда змін параметрів завжди обмежена вимогами одночасного передавання багатьох сигналів. Тобто, сигнальний простір, незалежно від його фізичної природи, містить множину областей, які не перетинаються, і кожному сигналу надається одна з таких областей значень, у межах якої може існувати даний сигнал.

Коливання – це відхилення від стану рівноваги параметра процесу. Тому будь-який сигнал є коливанням. За ступінню невизначеності коливання можна розділити на:

- детерміновані , тобто коливання, миттєві значення яких точно відомі будь-якої миті;

- випадкові, тобто коливання, миттєві значення яких неможливо передбачити з ймовірністю, що дорівнює 1.

Повна визначеність детермінованих коливань дозволяє використовувати їх як математичні та фізичні моделі під час теоретичного дослідження та експериментальних випробувань радіоелектронних засобів.

За характером зміни коливання можна розділити на:

- неперервні (аналогові) , тобто коливання що приймають будь-які миттєві значення в області існування;

- дискретні, - що мають лічену кількість припустимих значень (мінімально – 2 значення). Дискретні коливання – це ідеальна модель, бо миттєвий перехід будь-якої реальної фізичної системи з одного енергетичного стану до іншого є неможливим. Тому, будь-які реальні коливання – аналогові із скінченим часом переходу від одного припустимого значення до іншого.

10.2. Основні характеристики детермінованих коливань

10.2.1. Часові характеристики коливань

Амплітуда - найбільше значення коливання.

Тривалість - часовий інтервал між заздалегідь обумовленими значеннями коливання (часто – між

нульовими значеннями).

Період Т – найменший часовий інтервал між точками коливання з однаковими фазами, тобто періодичне коливання (повторюване коливання) можна записати як функцію часу (див. Рис. 10.1)

Періодичне коливання є «найбільш абстрактною» моделлю детермінованого коливання, бо, виходячи з попереднього виразу, воно не має ні початку, ні кінця. У будь-якому реальному випадку коливання має місце, поки діє джерело коливання, яке колись було ввімкнене. Така модель є дуже зручною для аналізу, бо вся інформація про параметри коливання міститься у одному його періоді. Реальне коливання можна вважати періодичним у разі виконання умови

,

де 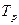- тривалість реалізації коливання, яку слід розуміти як час спостереження коливання.

Початкове запізнення (початкова затримка) - часовий інтервал між початком відліку часу та обумовленим значенням коливання. На Рис. 10.1 подано початкову затримку амплітуди коливання. Там же показано тривалість 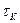на рівні , де .

10.2.2. Енергетичні характеристики коливань

Миттєва потужність, що виділяється на опорі величиною 1 Ом

. (10.1)

Миттєва потужність не адитивна (не відповідає принципу суперпозиції), тобто миттєва потужність суми двох коливань не дорівнює сумі їх миттєвих потужностей.

(10.2)

Енергія на інтервалі часу 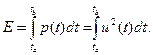(10.3)

Середня потужність на інтервалі (10.4)

Підставимо у (3) суму двох коливань (10.5)

де - взаємна енергія або енергія взаємодії двох коливань. Якщо виконується умова (10.6)

називаються ортогональними на інтервалі і для них

Приклад. На Рис. 10.2 подані два коливання: , ортогональні на будь-якому інтервалі часу, що містить ціле число періодів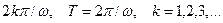

На інтервалі - коливання ортогональні, на інтервалі - не ортогональні.

Ортогональними є також функції синус та косинус одної частоти та цілократних частот на часовому інтервалі, що дорівнює цілому числу періодів найменшої частоти. На практиці часто використовується поняття приблизної ортогональності. Воно має місце за умови, наведеної вище - .

10.2.3. Кореляційні характеристики коливань

Автокореляційна функція коливання (АКФ)

(10.7)

- це функція, що свідчить про степінь зв’язку між коливанням та його копією, зсунутою у часі.

Якщо

На Рис. 10.3 продемонстровано утворення авторкореляційної функції за виразом (10.7) для прямокутного імпульсу з амплітудою та тривалістю . Функція дорівнює площі взаємного перекриття двох прямокутників і, відповідно, має вид симетричного трикутника з висотою (амплітудою) та тривалістю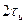

Взаємнокореляційна функція (ВКФ)

(10.8)

це функція, що свідчить про степінь зв’язку між різними коливаннями, наприклад, між коливаннями на вході та виході пристрою. Для нормування взаємнокореляційної функції застосовують коефіцієнт взаємної кореляції

(10.9)

Нормування дозволяє не враховувати підсилення або ослаблення коливання у пристрої, а визначати лише відмінність коливань на вході та виході, тобто оцінювати спотворення, що вносяться пристроєм. Максимальне значення свідчить про неспотворене передавання сигналу пристроєм. Порівнюючи вирази (6) та (8), можна зробити висновок, що ортогональні функції мають .

10.3. Моделі детермінованих коливань

Вище було вказано, що детерміновані коливання використовуються з метою дослідження характеристик радіоелектронних пристроїв щодо спотворень, які вони додають до сигналу під час проходження його через досліджуваний пристрій. Коливанням, що в найбільшій мірі відповідає поставленій меті, є періодичне синусоїдне (косинусоїдне) коливання. З одного боку, воно описує процеси обміну енергією у більшій частини енергомістких пристроїв, з іншого боку, має просте математичне подання та просто формується у реальних радіоелектронних пристроях.

Синусоїдне (косинусоїдне) коливання (Рис. 10.4) описується виразом

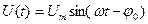, (10.10)

де - колова частота,

Т - період коливання,

- частота коливання,

- початкова фаза коливання,

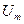- амплітуда коливання.

Синусоїдне коливання є зручною моделлю для опису стаціонарного режиму кола або пристрою. Але під час зміни дії або зміни параметрів елементів кола виникають перехідні процеси, для опису яких необхідно розглядати граничні умови, тобто стан елементів у момент початку змін. Саме для фіксації моментів часу початку дії введено модельну функцію ввімкнення.

Одинична функція (одиничний стрибок, функція Хевісайда, функція ввімкнення) (Рис. 10.5,а) описується виразом

. (10.11)

Для запису функції ввімкнення вісь часу розділено на дві ділянки – до стрибка та після нього. На межі цих ділянок, у момент 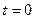, нескінченно швидко відбувається саме стрибок. Такий запис дозволяє розглядати одиничний стрибок як границю, до якої прямує зміна миттєвого значення будь-якої змінної, якщо швидкість зміни спрямувати до нескінченності. Якщо зсунути стрибок у часі на (Рис. 10.5,б), одержимо вираз

. (10.12)

Різниця двох зсунутих на час 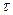одиничних функцій утворює прямокутний імпульс одиничної амплітуди, інакше, одиничний прямокутний імпульс тривалості 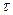(Рис. 10. 6)

(10.13)

У виразі (13) моменти стрибків віднесено до набуття складовими функціями одиничного значення. Важливо зазначити, що нульове значення коливання на часовому інтервалі є наслідком одночасної дії обох одиничних функцій, які існують у часі до нескінченності.

Помноження коливання 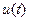на одиничну функцію є рівносильним ввімкненню його у момент

. (10.14)

Помноження коливання 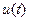на одиничний імпульс тривалості 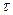створює імпульс, що має тривалість 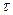і повторює форму 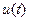у межах

(10.15)

Вираз (15) описує операцію комутації коливань, яка широко використовується під час формування радіоімпульсів, коли і .

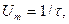Площа одиничного імпульсу, що описується виразом (13), дорівнює Якщо прийняти одержимо прямокутний імпульс тривалістю 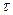одиничної площі, тобто

.

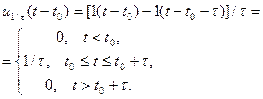
Якщо далі спрямувати , одержимо дельта-функцію (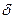-імпульс, функцію Дірака), графічне подання якої показано на Рис. 10.8.

(10.16)

тобто дельта-функція є нескінченно коротким імпульсом нескінченно великої амплітуди, але одиничної площі.

(10.17)

На Рис. 10.8 δ-імпульси показані стрілками, які символізують нескінченність амплітуди імпульсів та їх зосередженість на осі часу.

Властивості дельта-функції.

1. Дельта-функція є парною, тобто З виразу (17) та парності витікає, що

звідки

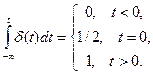
порівнюючи останній вираз з виразом (10), маємо

2. (10.18)

або (10.19)

Таким чином, використовуючи визначення дельта-функції, можна подати похідну від розривної функції у точці розриву. Необхідність визначення похідних від розривних функцій виникає під час аналізу імпульсної дії на кола, що містять реактивні елементи. Відомо (див. першу частину Посібника), що зв’язок між струмами і напругами у реактивних елементах є диференціальним. Тому, одержати вирази схемних функцій лінійних кіл можна, представляючи реакції кіл на розривну дію з використанням дельта-функцій відповідної площі. Визначимо, наприклад, похідну від імпульсної дії складної форми (див. Рис. 10.9)

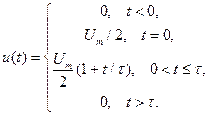
3. Враховуючи, що дельта-функція зосереджена у одній точці часової осі маємо

(10.19)

тобто, добуток будь-якої функції та дельта-функції є дельта-функцією, площа якої дорівнює значенню функції у точці 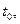звідки

(10.20)

Ця властивість називається фільтрувальною (пінцетною) властивістю дельта-функції. У радіоелектроніці процедура (20) називається стробуванням або взяттям вибірки з коливання і застосовується під час аналого-цифрового перетворення сигналів.

Усі розглянуті моделі використовуються для визначення реакції радіоелектронних пристроїв на дії складної форми. Лінійні кола підлягають принципу суперпозиції, тобто реакція кола на суму дій є сумою реакцій на кожну дію. Тому, якщо дія має складну форму, її можна розкласти на суму простіших, на які відома реакція кола, а далі, підсумкову реакцію кола визначати як суму відомих реакцій на простіші дії. Для розкладу коливань складної форми на простіші існує апарат перетворень Фур’є.

10.4. Розклад періодичного коливання в ряд Фур’є

Всяка періодична функція, що відповідає умові Дірихлє (тобто має на періоді скінчену кількість екстремумів та розривів), може бути подана сумою ряду ортогональних функцій, які називаються базисними

(10.21)

де - сталі коефіцієнти.

Властивість ортогональності мають, наприклад, тригонометричні функції sin, cos кратних аргументів. Розклад за цими функціями називається розкладом Фур’є у тригонометричному базисі.

Історично першим був саме тригонометричний базис, але сьогодні використовується ще не один десяток базисних функцій. Подання функції у вигляді суми ряду (21) є апроксимацією цієї функції. Завдання апроксимації, як і раніше, полягає у одержанні необхідного наближення до функції, яке здійснюється найбільш «економним» способом, тобто за допомогою скінченого ряду з найменшою кількістю членів. Це виявляється можливим за умови подібності форми функції f(t) та базисних функцій. Наприклад, розклад у тригонометричному базисі є найкращим для подання коливань у резонансних колах тощо. Таким чином, періодична функція у тригонометричному базисі подається сумою

(10.22)

де складові суми є косинусними коливаннями, частоти яких знаходяться у гармонічному співвідношенні, тобто вони цілократні основній частоті коливання 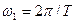. Ці складові носять назву гармонік. Коливання з частотою 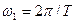називається першою гармонікою (к=1) і т.д. Амплітуди і фази гармонік повинні бути підібрані так, щоб рівність (22) виконувалась кожної миті існування коливання. Вираз (22) можна подати у іншій формі

(10.23)

У відповідності з теоремою Фур’є рівність у виразі (23) має місце, якщо коефіцієнти ряду визначити за формулами

(10.24)

Величина С₀ є середнім значенням коливання за період і називається його сталою складовою. Скориставшись формулами Ейлера

можна записати ряд Фур’є у комплексній формі

(10.25)

Комплексна амплітуда гармоніки знаходиться за виразом

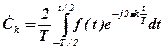. (10.26)

Підсумовування у виразі (25) ведеться по всіх к, як додатних, так і від’ємних, включаючи нуль, тобто у комплексній формі функція f(t) подається сумою гармонік з додатними та від’ємними частотами, що не мають фізичного змісту. Фактично це означає, що дійсний вектор миттєвих значень f(t) утворюється попарним підсумовуванням векторів гармонік, що обертаються з кутовими швидкостями у протилежні боки. Одержання такого підсумкового вектора для трьох гармонік подане на Рис. 10.10.

Сукупність гармонічних складових називається спектром В силу того, що спектр складається з окремих (дискретних) складових, розташованих тільки на частотах 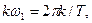він називається дискретним або лінійчатим. Графіки спектра відображаються на частотній площині і називаються амплітудною та фазовою спектральними діаграмами (див. Рис. 10.11). Амплітуди і фази гармонік на спектральних діаграмах мають вигляд 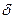-функцій, площа яких дорівнює амплітуді та фазі гармонік. Стала складова розташована на частоті 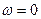і має фазу .

Читайте також:

1. I. ОБРАЗОВАНИЕ СОЕДИНЕННЫХ ШТАТОВ 14 страница
2. А. В. Дудник 1 страница
3. А. В. Дудник 10 страница
4. А. В. Дудник 11 страница
5. А. В. Дудник 12 страница
6. А. В. Дудник 2 страница
7. А. В. Дудник 3 страница
8. А. В. Дудник 4 страница
9. А. В. Дудник 5 страница
10. А. В. Дудник 6 страница
11. А. В. Дудник 7 страница
12. А. В. Дудник 8 страница

Переглядів: 855